
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
СИСТЕМАХ. Задачи, которые можно решать получать с помощью систем Поста, естественно связаны с множествами слов
|
|
|
|
РЕШЕНИЕ ЗАДАЧ В ПРОДУКЦИОННЫХ
Задачи, которые можно решать получать с помощью систем Поста, естественно связаны с множествами слов, выводимых в этих системах.
Простейший вопрос, который можно отнести к системе P - это вопрос о принадлежности конкретного слова множеству слов W P, выводимых в P. Такой вопрос записывается в виде:
″ 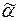 ÎW P ″?
ÎW P ″?
Ответом на него может быть только либо нет, либо да.
Естественный процесс поиска правильного ответа на этот вопрос состоит в нахождении вывода слова 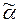 в системе P.
в системе P.
При этом если существует такой вывод W, то он может быть найден последовательным перебором всех конечных выводов в системе P.
Если же такой вывод отсутствует, а значит, слово 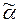 является невыводимым, то переборный алгоритм не позволяет получить ответ " нет" и поиск отрицательного ответа должен осуществляться другими методами.
является невыводимым, то переборный алгоритм не позволяет получить ответ " нет" и поиск отрицательного ответа должен осуществляться другими методами.
Обобщение рассмотренного типа задач, решаемых системами Поста, - это задачи, связанные с вопросом о выводимости в системе P слов, являющихся применениями заданного образца.
Для заданного образца t требуется получить ответ на вопрос о существовании такой подстановки Q, что t Q ÎW P.
Поскольку W P может содержать несколько различных применений t, то возможны несколько вариантов уточнения данного типа вопроса:
1) найти любое применение t, выводимое в системе P;
2) перечислить все применения t, выводимые в системе P;
3) найти применения t, обладающие дополнительным свойством.
Ответы на перечисленные варианты вопроса естественно представлять в виде последовательностей таких подстановок, что применение подстановки к t дает один из элементов ответа на вопрос.
Если же ни одно применение t не выводимо в системе Поста P, то ответом на поставленный вопрос является нет.
Как и в предыдущем случае, естественный алгоритм перебора всех конечных выводов в системе P не позволяет получить отрицательный ответ.
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 355; Нарушение авторских прав?; Мы поможем в написании вашей работы!