Доказательство окончено. Доказанная теорема позволяет сформулировать следующее утверждение: всякая интуитивно вычислимая числовая функция может быть вычислена подходящей системой

Доказанная теорема позволяет сформулировать следующее утверждение: всякая интуитивно вычислимая числовая функция может быть вычислена подходящей системой Поста.

Этот тезис носит название тезиса Поста. Его справедливость следует из тезиса Черча и доказанной возможности вычисления всякой частично-рекурсивной функции с помощью систем Поста.

Следовательно, функциональные возможности систем Поста такие же, как и у программ, составленных на одном из универсальных языков программирования. Совпадение множеств функций, вычисляемых системами Поста, и частично рекурсивных функций позволяет использовать знания, о рекурсивных функциях при изучении возможностей систем Поста. Например, рассмотрим задачу о выводимости в системах Поста множества слов, являющегося дополнением множества слов, выводимых в некоторой системе Поста.

Теорема 9.5. Существует система Поста P = (A, B, V, P), такая что множество (A È B)^* \ W_P не является множеством слов выводимых в системах Поста.

Доказательство.

Пусть U (n, x) универсальная частично рекурсивная функция для множества всех одноместных частично рекурсивных функций, определенная в главе 8. Рассмотрим вспомогательную функцию:

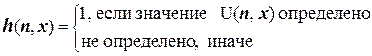
Поскольку функция h является вычислимой, то существует вычисляющая h система Поста П _h = (A _h, B _h, V _h, P _h), и не существует системы Поста П _H = (A _H, B _H, V _H, P _H), такой что A _h = A _H и 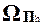= (A _h)* \ .

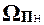Последнее утверждение является верным, поскольку существование системы П _H влечет разрешимость множества
A ₁={(n, x)½значение f_n (x) определено}, определенного в главе 8. Характеристическую функцию этого множества можно вычислять с помощью следующего алгоритма:

1. Пусть требуется определить принадлежность элемента множеству (n, x)Î A ₁.

2. С помощью алгоритмом построения всех конечных выводов в произвольных системах Поста организуем последовательное заполнение множеств 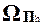и .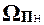

3. Продолжаем процесс до тех пор, пока 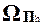или 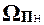не будет включено слово h (n, x) = 1.

4. Если слово h (n, x) = 1 добавляется во множество 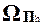, то (n, x)Î A ₁. Если слово h (n, x) = 1 добавляется во множество 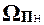, то (n, x)Ï A ₁.

Поскольку слово h (n, x) = 1 обязательно выводится в одной из систем Поста 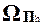или 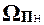, то приведенная процедура за конечное число шагов определяет принадлежность произвольной пары (n, x) множеству A ₁.

Дата добавления: 2015-03-31