Математическое моделирование процессов в электрических цепях

Математическое моделирование электромагнитного процесса в электрической цепи — это отображение и изучение в цепи на языке математических символов.

Модель установившегося процесса в цепи. Математическая модель установившегося процесса в цепи строится следую­щим образом:

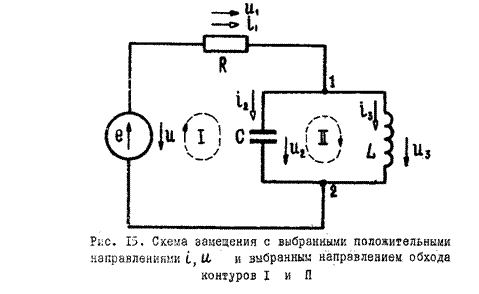
1. Для реальной цепи с учетом принятых допущений стро­ится схема замещения цепи;

2. Произвольно выбираются и обозначаются положитель­ные направления токов в ветвях и напряжений на элементах схемы замещения;

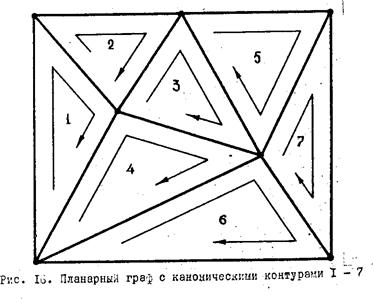
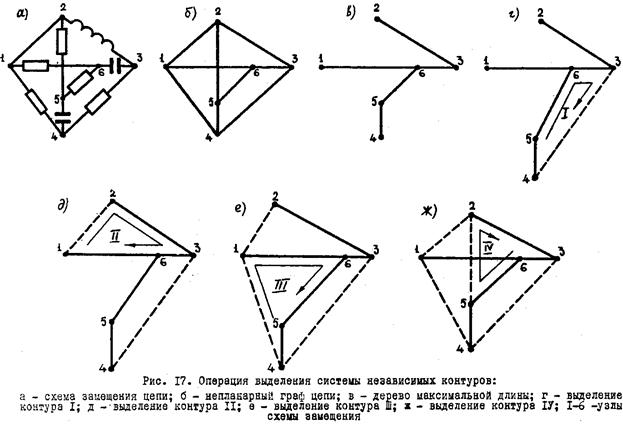
3. Выбираются системы независимых узлов и независимых контуров схемы замещения цепи. Если схема замещения цепи содержит q узлов и р ветвей, то независимых узлов в схеме будет q— 1; независимых контуров p — (q — 1);

4. Выбирается направление обхода контуров схемы заме­щения и обозначается для каждого независимого контура;

5. На основе применения законов Кирхгофа к независимым узлам и независимым контурам схемы замещения составляет­ся система уравнений состояния цепи. Она образуется урав­нениями для токов (число таких уравнений будет q — 1) и уравнениями для напряжений (их будет р— (q — 1));

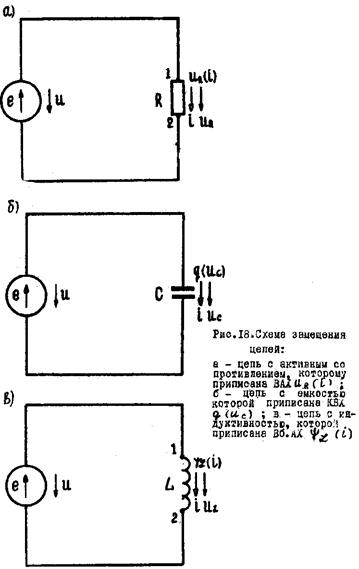
6. Записываются уравнения связи токов и напряжений на элементах схемы замещения.

Полученные системы уравнений состояния цепи (п. 5) и система уравнений связи (п. 6) образуют неявную математи­ческую модель установившегося процесса в цепи. Она обра­зуется системой уравнений состояния цепи и системой уравнений связи.

Системы уравнений, образующие неявную математическую модель установившегося процесса, совместно решаются отно­сительно неизвестных физических величин — токов и напря­жений элементов схемы замещения. Система полученных ре­шений для токов и напряжений элементов образует явную математическую модель установившегося процесса в цепи. Решениями устанавливаются законы изменения токов и на­пряжений элементов во времени. Они позволяют качественно и количественно оценить протекание установившегося процес­са в цепи.

Модель переходного процесса. Математическая модель пе­реходного процесса в цепи строится по той же методике (п. 1—6), что и модель установившегося процесса; она строится для момента времени после коммутации цепи.

К полученной системе уравнений состояния цепи (п. 5) и системе уравнений связи (п. 6) должна быть добавлена система начальных условий. Она записывается на основании за­конов коммутации цепи для момента времени перед комму­тацией цепи.

Таким образом, неявная математическая модель переход­ного процесса в цепи образуется системами: уравнений состоя­ния цепи (п. 5), уравнений связи (п. 6); начальных условий.

Совместное решение систем уравнений, образующих неявную математическую модель переходного процесса в цепи, по­зволит установить законы изменения токов и напряжений эле­ментов во время переходного процесса. Полученные решения образуют явную математическую модель переходного процес­са в цепи. Они позволяют рассмотреть характер изменения то­ков и напряжений элементов во время протекания переход­ного процесса в цепи.

Моделирование процессов с использованием функций-ори­гиналов и функций-изображений. Математические модели ус­тановившихся и переходных процессов в цепях могут состав­ляться и решаться относительно искомых напряжений токов, являющихся действительными функциями действитель­ной переменной t. Их записывают u (t), i (t) и называют функ­циями-оригиналами или оригиналами. В этом случае говорят, что моделирование процессов от начала до конца осуществля­ется во временной области.

Модель процесса может быть составлена и решаться для напряжений и токов, предварительно представленных через функции-изображения этих величин. На этом основан ком­плексный метод расчета установившихся процессов в цепях синусоидального тока, операторный, частотный и другие ме­тоды расчета переходных процессов. Полученные решения за­тем вновь переводятся во временную область, т. е. от функ­ций-изображений после получения решения вновь переходят к функциям-оригиналам.

Оба этих подхода широко используются при решении за­дач.

Контрольные вопросы

1. По какому признаку процессы в электрических цепях подразделяют­ся на установившиеся и переходные? Какой процесс в цепи называют установившимся, а какой — переходным?

2. Что понимается под состоянием электрической цепи в данный мо­мент времени или в данном интервале времени?

3. Какие три группы законов определяют развитие и протекание электромагнитного процесса в цепи?

4. Какие законы характеризуют процесс в цепи как в целом? Как словесно формулируются и математически записываются эти законы?

5. Сколько независимых уравнений можно составить на основании вменения закона Кирхгофа для токов в узлах схемы замещения?

6. Сколько независимых уравнений необходимо составлять на основании применения закона Кирхгофа для напряжений в контурах схемы?

7. Как выбирается система независимых контуров при использовании графа цепи?

8. Как математически записать связь тока и напряжения в линейных сопротивлении, емкости, индуктивности и взаимной индуктивности?

9. Как математически записать выражения для энергии и мгновенной мощности в нелинейных и линейных сопротивлении, емкости и индуктив­ности?

10. В чем состоит физический смысл понятий — электрическое сопро­тивление, емкость и индуктивность?

11. Как формулируются законы коммутации электрических цепей?

12. Что понимается под целевой функцией, отвечающей законам элек­трических цепей?

13. Как строится математическая модель установившегося процесса в цепи?

14. Как строится математическая модель переходного процесса в цепи?

Дата добавления: 2015-03-31