
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение
|
|
|
|
Примитивно-рекурсивные функции
ОПРЕДЕЛЕНИЕ
Функции, получаемые из простейших функций с помощью конечного числа применений операции суперпозиции, называются элементарными функциями.
Всякая элементарная функция является вычислимой.
Пример. Функция f (x) = x + 2 является элементарной, так как f (x) = S (S (x)).
Элементарными являются, в частности, все функции константы.
Например, функция f (x) = k, где k - некоторое число из N, может быть выражена следующей суперпозицией:
S (... S (O (x)...), в которой функция следования S применяется k раз.
Упражнение. Показать, что если f (x 1,..., xn) - это элементарная функция, то она растет не быстрее, чем некоторая линейная функция.
Существуют вычислимые числовые функции, которые не являются элементарными.
Например, функция f (x) = x 2 не является элементарной.
Пусть заданы функции:
g (x 1,..., xn) и h (x 1,..., xn, xn + 1, xn + 2).
Функция f (x 1,..., xn+ 1) получается из функций g и h с помощью операции примитивной рекурсии, если справедливы соотношения:
f (x 1,..., xn, 0) = g (x 1,..., xn); (1)
f (x 1,..., xn, y + 1) = h (x 1,..., xn, y, f (x 1,..., xn, y)). (2)
Соотношения (1) и (2) называются схемой примитивной рекурсии. Соотношение (1) задает граничное условие, а соотношение (2) рекурсивно выражает значения функции f через другое значение этой функции.
Переменные x 1,..., xn в схеме примитивной рекурсии представляют собой параметры. При этом допускается отсутствие параметров. В последнем случае функция g не имеет существенных переменных и является константой. Переменные xn+ 1 и xn+ 2 называются соответственно переменной рекурсии и переменной для рекурсивного вызова.
Предположим, что функции g и h являются вычислимыми. В этом случае функция f также является вычислимой.
Действительно, для нахождения значения f (x 1,..., xn+ 1) можно воспользоваться следующей процедурой:
1. Вычислить значение f (x 1,..., xn, 0), используя алгоритм вычисления функции g и соотношение (1) схемы примитивной рекурсии.
2. Используя соотношение (2) и алгоритм вычисления функции h, можно последовательно вычислить значения
f (x 1,..., xn, 1),..., f (x 1,..., xn, xn+ 1).
Функции, получаемые из простейших функций с помощью конечного числа применений операций суперпозиции и примитивной рекурсии, называются примитивно-рекурсивными.
Из приведенного определения следует, что всякая примитивно-рекурсивная функция является всюду определенной функцией. Кроме того, все примитивно-рекурсивные функции вычислимы.
Упражнение. Показать, что если f (x 1, x 2) является примитивно-рекурсивной функцией, если она выражается через примитивно-рекурсивные функции g и h с помощью соотношений
f (0, x) = g (x); (1)
f (y + 1, x) = h (x, y, f (y, x)). (2)
Доказательство справедливости приведенного в упражнении утверждения обосновывать примитивную рекурсивность функций, определяемых рекурсивными схемами, в которых рекурсия ведется по произвольной переменной.
Рассмотрим примеры примитивно-рекурсивных функций.
1. Сумма f (x, у) = x + у задается следующей схемой примитивной рекурсии:
f (x, 0) =  (x);
(x);
f (x, у + 1) = S (f (x, у)).
То есть f (x, у) получается из элементарных функций g (x 1)=  (x 1) и h (x 1, x 2, x 3) = S (
(x 1) и h (x 1, x 2, x 3) = S (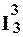 (x 1, x 2, x 3)) с помощью операции примитивной рекурсии и поэтому является примитивно-рекурсивной.
(x 1, x 2, x 3)) с помощью операции примитивной рекурсии и поэтому является примитивно-рекурсивной.
2. Произведение p (x, у) = x ´ у задается схемами:
p (x, 0) = O (x);
p (x, у + 1) = x + p (x, у).
Здесь p выражается через функции O (x) и f ( (x 1, x 2, x 3),
(x 1, x 2, x 3), 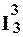 (x 1, x 2, x 3)), где f - это примитивно-рекурсивная функция из предыдущего примера.
(x 1, x 2, x 3)), где f - это примитивно-рекурсивная функция из предыдущего примера.
3. Экспонента e (x) = 2 x может быть задана соотношениями:
e (0) = S (0);
e (x + 1) = 2× e (x).
Функции S (0 (y)) и 2 y - примитивно-рекурсивные. Поэтому функция e (x) также является примитивно-рекурсивной.
4. Функции sg (x) и 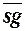 (x), определяемые как:
(x), определяемые как:
sg (x) =  и
и 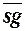 (x) =
(x) =  , задаются следующими схемами:
, задаются следующими схемами:
sg (0) = 0; 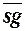 (x) = 1;
(x) = 1;
sg (x + 1) = 1. 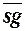 (x + 1) = 0.
(x + 1) = 0.
5. Функция уменьшения на единицу d (x) = x - 1 определяется как:
d (0) = 0;
d (x + 1) = x.
6. Функция усеченного вычитания m (x, у) = x - у:
m (x, 0) = x;
m (x, у + 1) = d (m (x, у)).
Функции из примеров 5 и 6 являются аналогами арифметического вычитания для множества целых неотрицательных чисел. Такие функции по определению равны нулю, если вычитаемое больше уменьшаемого.
Используя приведенные ранее функции, можно доказывать примитивную рекурсивность и других известных числовых функций.
Например, рассмотрим функцию mod (x, y), принимающую значение, равное остатку от деления числа x на число y.
Для определенности положим, что при делении на нуль остаток всегда равен 0.
Определим mod (x, y) схемой:
mod (0, y) = 0; (1)
mod (x + 1, y) = (mod (x, y)+ 1)× sg (y - (mod (x, y)+ 1)). (2)
Здесь рекурсия ведется по первой переменной.
В соотношении (2) реализовано очевидное свойство остатка от деления значения x + 1 на y, которое можно выразить следующим соотношением:
mod (x + 1, y) либо равен mod (x, y)+ 1, если mod (x, y) < y, либо равен 0, в случае, когда mod (x, y) = y.
Аналогичными соотношениями можно выразить функцию для целочисленного деления div (x, y).
Для определенности будем считать, что div (x, 0) = x, поскольку функция целочисленного деления не является всюду определенной.
div (0, y) = 0;
div (x + 1, y) = div (x, y)+ 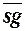 (y -(mod (x, y)+1)).
(y -(mod (x, y)+1)).
В приведенных определениях функций использовалась рекурсия по первой переменной. Это не соответствует схеме примитивной рекурсии, в которой переменная рекурсии - это последняя переменная определяемой функции. Тем не менее, рекурсия по первой переменной легко может быть сведена к рекурсии по последней переменной. Для этого достаточно выполнить перестановку переменных с помощью операции суперпозиции.
Например, для функции mod (x, y) необходимо образовать вспомогательную функцию g (x, y)= mod (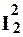 (x, y),
(x, y), 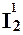 (x, y)). Такая функция может быть выражена с помощью схемы примитивной рекурсии.
(x, y)). Такая функция может быть выражена с помощью схемы примитивной рекурсии.
Поэтому mod также является примитивно-рекурсивной функцией, поскольку получается из примитивно-рекурсивной функции g обратной перестановкой переменных.
При обосновании примитивной рекурсивности некоторых функций могут оказаться полезными свойства, доказываемые в следующих теоремах.
|
|
|
|
|
Дата добавления: 2015-03-31; Просмотров: 1095; Нарушение авторских прав?; Мы поможем в написании вашей работы!