Функций

НУМЕРАЦИЯ ЧАСТИЧНО-РЕКУРСИВНЫХ

ОПРЕДЕЛЕНИЕ

Функции, получаемые из простейших с помощью конечного числа применений операций суперпозиции, примитивной рекурсии и минимизации, называются частично-рекурсивными функциями.

Все частично-рекурсивные функции являются вычислимыми, поскольку вычислимы элементарные функции и все операции, применяемые в определениях частично рекурсивных функций.

8.3. ТЕЗИС ЧЁРЧА

Частично-рекурсивные функции - это класс числовых функций, представляемых точно определенными формальными средствами.

Связь класса частично-рекурсивных функций и интуитивно вычислимых числовых функций устанавливается в форме следующего утверждения, носящего характер естественно - научной гипотезы.

Класс всех интуитивно вычислимых числовых функций

совпадает с классом частично-рекурсивных функций

Приведенное утверждение носит название тезиса Чёрча, по имени сформулировавшего этот тезис американского математика.

Данный тезис связывает интуитивное понятие вычислимости числовых функций и формальное определение частичной рекурсивности. Поэтому он является недоказуемым.

О справедливости тезиса Чёрча свидетельствуют следующие имеющиеся факты:

1) для всякой конкретной числовой функции удается построить её рекурсивное определение;

2) многочисленные попытки построить другие общие формальные определения вычислимой числовой функции всегда приводили к классам вычислимых функций, которые содержатся (в том числе совпадают) в классе частично рекурсивных функций.

Ниже будет построена специальная последовательность, состоящая из всех частично-рекурсивных функций.

Для этого полное определение произвольной частично- рекурсивной функции представляется в виде специального нагруженного дерева.

Все такие деревья нумеруются с помощью неотрицательных целых чисел, а представляемые ими частично-рекурсивные функции образуют последовательность всех таких функций, в которую они входят в порядке возрастания номеров соответствующих деревьев.

Будем считать, что для обозначения переменных функций используются только следующие символы: x ₁,..., x_i,...

При разметке вершин деревьев используются следующие символы:

1) C, P, M -для обозначения операций суперпозиции, примитивной рекурсии и минимизации;

2) 1 -для записи индексов переменных в унарной системе;

3) I, S, O - для обозначения простейших функций.

Определим деревья, представляющие схемы определения частично-рекурсивных функций, с помощью следующих правил:

1. Функции O (x_i), S (x_i) и (x_{i 1},..., x _{i n} ) представляются следующими деревьями:

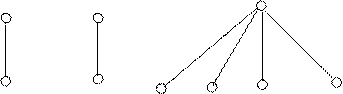
Дата добавления: 2015-03-31