Доказательство. Доказательство окончено

ТЕОРЕМА 8.6

ПРОБЛЕМА ЭКВИВАЛЕНТНОСТИ

Доказательство окончено.

Эквивалентность двух произвольных программ состоит в том, что эти программы вычисляют одну и ту же функцию.

Определим множество R ₃ = {(m, n) | f_m º f_n }.

То есть это множество пар номеров равных функций в нумерации всех одноместных частично-рекурсивных функций.

Если множество R ₃ является разрешимым, то существует разрешающий алгоритм для проблемы эквивалентности программ.

Множество R ₃ является неразрешимым.

Предположим противное, т.е. множество R ₃ является разрешимым, а его характеристическая функция

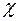(n, m) = 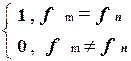- вычислимая.

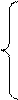Рассмотрим преобразование функций последовательности (3), которое всякой функции f_i ставит в соответствие частичную функцию:

1, значение f_i (x) определено

d_i (x) =

-, значение f_i (x) не определено.

Справедливо следующее свойство: функция d_i совпадает с функцией, тождественно равной единице тогда и только тогда, когда функция f_i является всюду определенной.

По определению последовательности (3) и нумерации n существует метод, который по n номеру i произвольной функции f_i позволяет построить схему определения этой функции.

Достроим полученную схему до определения функции d_i, например, с помощью соотношения:

d_i (x) = (f_i (x)) + 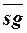(f_i (x)).

Тогда функция p (x), определяемая соотношением:

" i (p (i) = k 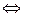d_i = f _k),

является вычислимой.

Содержательно отображение p преобразует n номер произвольной функции f_i и F¹ в некоторый конкретный n номер, равный p (i), такой функции в той же последовательности (3), которая совпадает с d_i. Для вычисления значений функции p можно воспользоваться следующей схемой:

1. Построим дерево D f_i определения функции f_i (x).

2. Достроим D f_i в дерево D, представляющее определение функции f_i (x)) + 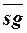(f_i (x).

3. По дереву D построим его код .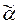

4. Найдем код 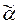в последовательности (1) кодов деревьев определений частично-рекурсивных функций.

5. Если k - номер найденного слова в последовательности (1), то положим p (i) = k.

Возьмем некоторый номер i ₀ всюду определенной функции, которая всегда принимает значение 1.

Рассмотрим функцию:

y(x) = c(i ₀, p (x)).

Очевидно, что она является вычислимой. Кроме того:

y(x) = .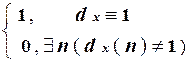

Из этого следует, что y (x) = 1 тогда и только тогда, когда f_i - всюду определенная функция, т.е.

y(x) = .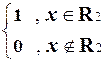

Значит y- это вычислимая характеристическая функция множества R ₂. Это противоречит доказанной ранее теореме о неразрешимости данного множества.

Следовательно, предположение о разрешимости множества R ₃ неверно.

Дата добавления: 2015-03-31