Статистическая мера информации

В этом подходе используется понятие энтропии как меры неопределенность, учитывающей вероятность появления того или иного сообщения. Учитывает конкретные условия применения систем.

Статистическая мера – вероятностный подход к определению количества информации.

1948 год – Клод Шеннон.

(N – количество возможных опытов, k – количество типов опытов, i – iтый исход, повторяющийся n_i раз, p_i – вероятность появления опыта с iтым исходом, I_i – количество информации)

Средняя информация доставляемая одним опытом определяется:

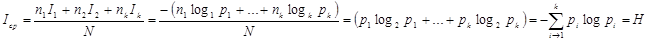Свойства энтропии:

1) Всегда неотрицательна

2) Обращается в ноль, когда одно из состояний системы достоверно, а остальные невозможны

3) Если события равновероятны, то количество информации шеннона равно количеству информации по Хартли

4) Энтропия системы с конечным множеством состояний достигает максимального значения, когда эти состояния равновероятны, а при увеличении числа состояний энтропия повышается.

Количество информации – уменьшение энтропии вследствие опыта или какого-либо акта познания.

1) Если неопределенность снимается полностью количество информации равно энтропии. I=H

2) В случае неполного разрешения имеет место быть частичная информация, которая определяется как разность между начальной и конечной энтропией I=H₁-H₂

3) Наибольшее количество информации получается, когда полностью снимается неопределенность.

Абсолютная избыточность информации:

Относительная избыточность информации: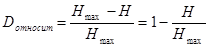

Дата добавления: 2015-04-23