Квантование по уровню. Теорема Котельникова

Дискретизация информации.

Дискретизация (квантование по времени) состоит в преобразовании сигнала X(t) непрерывного аргумента t в сигналах X(t_i) дискретного аргумента.

Воспроизводящая функция V(t) – функция, полученная в результате восстановления по значениям X(t_i).

Шаг дискретизации: Δt_i= t_i - t_i -1 влияет на точность восстановления, воспроизведения функции.

Частота дискретизации выбирается с учетом требуемой точности последующего восстановления сигнала по его мгновенным значениям в момент времени t_i.

Оптимальная дискретизация – дискретизация, которая обеспечивает представление исходного сигнала с заданной точностью при минимальном количестве отсчетов.

Методы дискретизации и восстановление. Классификация:

1) По регулярности отсчета:

· Равномерная Δt=const

· Неравномерная Δ t_i=var (адаптивная и программируемая)

2) По критерию оценки точности:

· Критерии наибольшего отклонения

· Среднеквадратический критерий

· Интегральный критерий

· Вероятностный критерий

3) По типу базисных (приближающихся) функций

4) По типу воспроизводящих функций:

· Ряды Фурье и Котельникова

· Полиномы Чебышева и Лежандра

· Функции Уолша и Хоара

· Степенные полиномы

· Гипергеометрические функции

Квантование (по уровню) состоит в преобразовании непрерывного сигнала множества значений X(t) в дискретное множество значений X_k, k=0, 1, 2 … (m-1). X_k [X_min; X_max]

Квантование по уровню - это процесс замены непрерывной функции ее отдельными значениями, отстоящими друг от друга на конечный интервал (уровень). При квантовании значение функции в произвольный момент времени заменяется ее ближайшим значением, называемым уровнем квантования. Интервал между двумя дискретными значениями уровней называется шагом квантования (q).

Квантование сигнала по уровню: а - с постоянным шагом квантования б - погрешности квантования в - квантование с переменным шагом

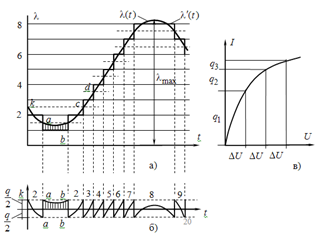
В соответствии с графиком изменение функции X(t)ее истинные значения определяются в виде заранее заданных дискретных уровней 1, 2, 3.. Функция в моменты отсчета может задаваться либо точно (X(t_i+1); X(t_i-1)) либо с некоторой погрешностью X(t_i). Квантование по уровню может быть:

· Равномерным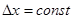

· Неравномерным

Уровень квантования можно выразить двумя способами:

1) Сигнал X(t_i) отождествляется с ближайшим уровнем квантования

2) Сигнал X(t_i) отождествляется с ближайшим меньшим или большим уровнем квантования

Уровни квантования кодируются в двоичной системе счисления.

Теорема Котельникова:

Непрерывная функция времени F(t), не содержащая частот выше f_max, полностью определяется конечным числом мгновенных значений F(kΔt) в точках, стоящих друг от друга на шаг дискретизации.

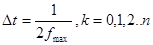
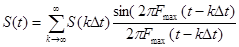
Дата добавления: 2015-04-23