Логическая функция двух переменных. Правила построения совершенной дизъюнктивной нормальной формы

		F5	F6	F7	F8	F9	F10	F11
X1	X2	X1^X2	X1VX2	X1→X2	X1 X2	X1↔X2	X1IX2	X1↓X2

Конъюнкция (логическое умножение) – функция F5 (X1;X2), которая истинна тогда и только тогда когда и X1 и X2 истины. Также называется функцией И.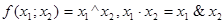

Дизъюнкция (логическое сложение) – функция F6 (X1;X2), которая истинна тогда и только тогда когда истинны или X1 или X2 или обе переменные вместе. Функция ИЛИ. F(x)=X1+X2=X1vX2

Функция сложения по модулю 2 – функция F8 (X1;X2) является истинной, когда истинны X1 или X2 в отдельности. F(x)= X1 X2

Штрих Шеффера – функция F10 (X1;X2), которая ложна тогда и только тогда когда X1 и X2 истины. F(x)= X1IX2

Функция (стрелка) Пирса - функция F11 (X1;X2),которая истинна только когда X1 и X2 ложны. Функция НЕ ИЛИ. F(x)= X1↓X2

Функция равнозначности - функция F9 (X1;X2) принимает значение единица, истина на всех равных значениях.

Импликация (следование) - функция F7 (X1;X2). Это очень важная функция, особенно в логике. Ее можно рассматривать следующим образом: если х = 0 (т. е. х “ложно”), то из этого факта можно вывести и “ложь”, и “истину” (и это будет правильно), если у = 1 (т. е. у “истинно”), то истина выводится и из “лжи” и из “истины”, и это тоже правильно. Только вывод “из истины ложь” является неверным. Заметим, что любая теорема всегда фактически содержит эту логическую функцию.

В алгебре Булля используются функции И, ИЛИ, НЕ – функционально полный набор логических функций с помощью которого можно построить любую логическую функцию.

Свойства элементарных функций алгебры логики:

1.

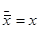
2. x+x=x, xx=x

3. x+0=x

4. x+1=x

5. x∙0=0

6. x∙1=x

7.

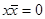
8.

Совершенная дизъюнктивная нормальная форма – функция алгебры логики, представленная в виде дизъюнкции элементарных конъюнкций, ранг которых равен числу независимых переменных.

Получение СНДФ:

1. Из таблицы истинности выбираются все наборы значений аргументов Х1,Х2..Хnна которых функция равна 1

2. Для каждого из таких выборов составляется конъюнкция из n переменных. При этом аргумент принимающий значение 0 входит в конъюнкцию с отрицанием, а значение 1 – без отрицания

3. Полученные конъюнкции соединяются знаком дизъюнкции

Дата добавления: 2015-04-23