
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные даты и события. 1 страница
|
|
|
|
Т.обр.
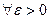


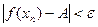 ., то есть
., то есть 
17) Арифметические свойства предела функции.
Теорема: Если существуют  и
и  , то:
, то:
1). 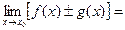

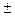
 .
.
2).  =
= 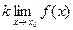 (
( - постоянная).
- постоянная).
3). 
 *
*  .
.
4). 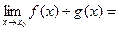

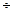
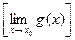 , если
, если  .
.
Доказательства:
Доопределив по непрерывности функции 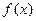 и
и  в точке
в точке 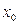 , положив
, положив 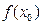 =
=  и
и 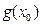 =
=  (это изменение функций не влияет на их пределы). В точке
(это изменение функций не влияет на их пределы). В точке 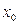 будут непрерывны функции
будут непрерывны функции 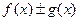 ,
,  ,
,  ,
,  (так как
(так как 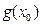 =
=  . Поэтому в силу равенства
. Поэтому в силу равенства  =
= 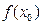 получим:
получим:
1). 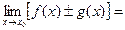
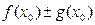 =
= 
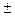
 .
.
2).  =
=  =
= 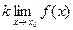
3). 
 =
=  *
*  .
.
4). 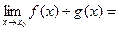
 =
= 
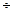
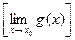 .
.
18) Свойства предела функции: единственность предела; ограниченность функции, имеющей предел.
19) Свойства предела функции: предельные переходы в неравенства.
20) Односторонние пределы.
21) Первый замечательный предел.
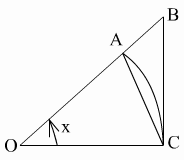

Для доказательства возьмем вектор  окружности радиуса 1 с центральным углом, равным
окружности радиуса 1 с центральным углом, равным 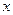 (радиан),
(радиан), 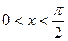 и проведем
и проведем  . Тогда пл.
. Тогда пл. 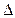
 < пл. сект.
< пл. сект.  < пл.
< пл. 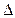
 или
или  . Разделив все части этого неравенства на
. Разделив все части этого неравенства на 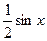 > 0, получим
> 0, получим
 или
или  . Это неравенство, доказанное для любых
. Это неравенство, доказанное для любых 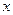 из интервала (0;
из интервала (0;  ), верно для любого
), верно для любого 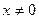 из интервала (-
из интервала (-  ;
;  ) в силу четности функций, входящих в это неравенство.
) в силу четности функций, входящих в это неравенство.
Докажем, что 
( ) при
) при 
А раз  и
и 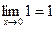 , то
, то  .
.
Кроме того:  =
= 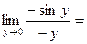 1
1
22) Второй замечательный предел.

 .
.
На первый взгляд кажется, что  при
при  имеет пределом единицу (так как 1+
имеет пределом единицу (так как 1+ 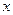 при
при  имеет пределом единицу, а единица в любой степени есть единица). Но в степень
имеет пределом единицу, а единица в любой степени есть единица). Но в степень  возводится 1+
возводится 1+ 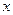 , а не единица. И вот из-за этой бесконечно малой добавки
, а не единица. И вот из-за этой бесконечно малой добавки 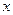 предел не равен единице. Чтобы приблизительно представить себе поведение функции
предел не равен единице. Чтобы приблизительно представить себе поведение функции  при малых
при малых 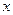 приведем таблицу значений этой функции:
приведем таблицу значений этой функции:
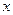
| 1/2 | 1/3 | 1/4 | 0.01 | 0.001 |

| 2.25 | 2.37… | 2.44… | 2.7047… | 2.7169… |
Из этой таблицы видно, что с уменьшением 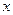 функция увеличивается. Оказывается, что это имеет место для всех
функция увеличивается. Оказывается, что это имеет место для всех 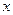 >0, а из этого следует, что функция имеет предел.
>0, а из этого следует, что функция имеет предел.
Доказательство:
Рассмотрим этот предел, как предел функции натурального аргумента на бесконечность. Тогда:
По определению Гейне:
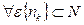

 =
= 

 =
= 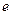
Вычислим 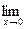
 . Рассмотрим
. Рассмотрим 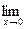
 =
=  =
= 
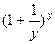 .
.
По определению Гейне рассмотрим 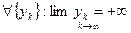 .
.
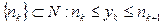
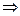




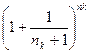
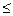
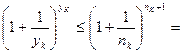
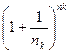 *
* 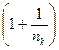
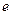
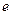
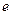
То есть 
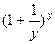 =
= 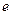 =
= 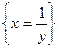 =
= 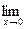
 .
.

 Также
Также 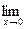
 =
= 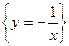 =
= 
 =
= 
 =
= 

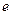 1
1
23) Б.м. функции и их свойства.
Определение: 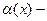 бесконечно малая функция при
бесконечно малая функция при  , если
, если 
 .
.
Определение: Пусть  и
и  - бесконечно малые функции при
- бесконечно малые функции при  . Тогда:
. Тогда:
1)  и
и  эквивалентны при
эквивалентны при  (
( ~
~  ,
,  ), если
), если 
 .
.
2)  ,
,  - бесконечно малые одного порядка малости при
- бесконечно малые одного порядка малости при  , если
, если 
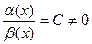 . 3)
. 3)  - бесконечно малая более высокого порядка малость, чем
- бесконечно малая более высокого порядка малость, чем  .
.
( =
= 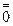 (
( ),
),  ), если
), если 
 .
.
4).  имеет
имеет  -й порядок малости относительно
-й порядок малости относительно  при
при  , если
, если 
 .
.
5).  называется ограниченной относительно бесконечно малой функции
называется ограниченной относительно бесконечно малой функции  при
при  , если
, если 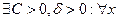

 .
.
Примеры:
1).  при
при  .
.
2).  (
( ,
, 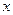 -бесконечные малости одного порядка).
-бесконечные малости одного порядка).

 3).
3).  (
(
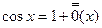 )
)
1 0
4).  …
…
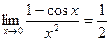 (
(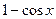 )- 2-й порядок малости относительно
)- 2-й порядок малости относительно 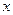 при
при  .
.
5). 

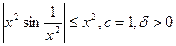 - произвольная.
- произвольная.
24) Б.б. функции и их связь с б.м. функциями.
25) Сравнение б.м. функций. Примеры.
Определение: 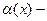 бесконечно малая функция при
бесконечно малая функция при  , если
, если 
 .
.
Определение: Пусть  и
и  - бесконечно малые функции при
- бесконечно малые функции при  . Тогда:
. Тогда:
1)  и
и  эквивалентны при
эквивалентны при  (
( ~
~  ,
,  ), если
), если 
 .
.
2)  ,
,  - бесконечно малые одного порядка малости при
- бесконечно малые одного порядка малости при  , если
, если 
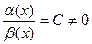 . 3)
. 3)  - бесконечно малая более высокого порядка малость, чем
- бесконечно малая более высокого порядка малость, чем  .
.
( =
= 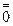 (
( ),
),  ), если
), если 
 .
.
4).  имеет
имеет  -й порядок малости относительно
-й порядок малости относительно  при
при  , если
, если 
 .
.
5).  называется ограниченной относительно бесконечно малой функции
называется ограниченной относительно бесконечно малой функции  при
при  , если
, если 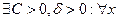

 .
.
Примеры:
1).  при
при  .
.
2).  (
( ,
, 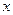 -бесконечные малости одного порядка).
-бесконечные малости одного порядка).

 3).
3).  (
(
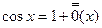 )
)
1 0
4).  …
…
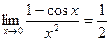 (
(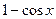 )- 2-й порядок малости относительно
)- 2-й порядок малости относительно 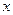 при
при  .
.
5). 

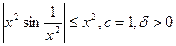 - произвольная.
- произвольная.
26) Эквивалентные б.м. функции (таблица). Теорема об эквивалентных б.м. функциях.
Определение: функция  называется бесконечно малой при
называется бесконечно малой при  , если
, если 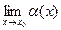 =0.
=0.
Теорема (критерий эквивалентности):
Пусть  ,
,  -бесконечно малые функции при
-бесконечно малые функции при  .
.
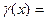
 -
-  . Тогда
. Тогда  ~
~  при
при 
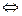
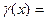
 .
.
Доказательства:
(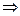 ). Пусть
). Пусть  ~
~  ,
,  , то есть
, то есть 
 .
.

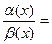


 =0,
=0,
то есть 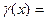
 .
.
( ).
). 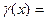
 .,
., 
 .
.

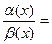
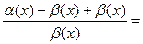

 =1.
=1.
Теорема (о замене на эквивалентные):
Пусть функция  ~
~  ,
,  ~
~  при
при  и существует
и существует 
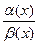 , тогда существует и
, тогда существует и 
 =
= 
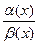 . То есть выражение или функцию можно заменять на эквивалентное.
. То есть выражение или функцию можно заменять на эквивалентное.
|
|
|
|
|
Дата добавления: 2015-04-23; Просмотров: 430; Нарушение авторских прав?; Мы поможем в написании вашей работы!