Алгоритмы факторизации. Метод Полларда

Задача факторизации - разложение на множители.

ρ - Метод Полларда.

С помощью этого метода было впервые факторизовано число Ферма. Впервые этот алгоритм был предложен Дж. Поллардом в 1975 г. Суть его заключается в следующем: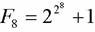

1. Выбираем отображение, где - кольцо вычетов по модулю n. В качестве функции обычно берут полиномы степени ≥2 (например).

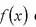
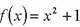
2. Выбираем некоторое число и строим рекурсивную последовательность по следующему принципу .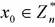

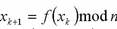3. Для некоторых номеров i и j вычисляем 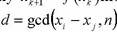. Если или , то рассматриваем другую пару 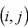. Если , то d – делитель числа n.

Как видим, алгоритм может оказаться довольно громоздким из-за большого количества пар. Эта проблема решаема с помощью некоторых способов выбора номеров i и j. Рассмотрим некоторые из них: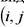

1., т.е.

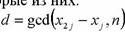
2. Если j удовлетворяет условию, то берут

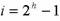
Если окажется, что алгоритм не нашел делителя, то можно попробовать другие функции f, например, где с – некоторая константа.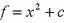

Сложность этого алгоритма оценивается, как битовых операций. Существует теорема, которая формулируется так: Пусть n – составное число, 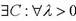вероятность того, что метод Полларда не сможет найти нетривиальный делитель n за время не превышает величину.

ρ - Метод Полларда обычно используется для нахождения небольших делителей числа n.

(P-1)-метод Полларда.

Прежде чем начать рассмотрение этого алгоритма введем определение: будем говорить, что число k является B-степенно-гладким для некоторого B>0, если: m – простое и является делителем числа k, выполнено услови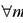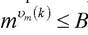е , где - наибольшее число такое, что 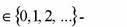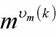делит k.

Теперь непосредственно сам алгоритм:

1. Исходя из возможностей нашей вычислительной машины, выбираем границу гладкости B. Обычно B~.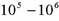

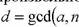
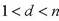2. Выбираем произвольное целое число a, удовлетворяющее условию , и вычисляем. Если , то d – искомый делитель.

3. Строим таблицу всех простых чисел и для каждого такого числа находим 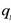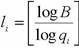, т.е..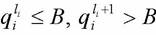

4. Вычисляем

5. Находим 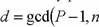. Если , то d – искомый делитель, иначе алгоритм не смог найти делитель. В этом случае можно взять другое основание a или границу гладкости.

Оценка сложности этого метода в худшем случае составляет 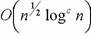арифметических операций. Однако в некоторых случаях этот алгоритм может довольно быстро найти делитель n.

Дата добавления: 2015-04-23