Представить на языке программирования вычислительный алгоритм, записанный в виде блок-схемы. (Получить результат в виде значения переменной.)

С помощью электронной таблицы вычислить значение функции, заданной рекуррентным соотношением

Основные понятия и операции формальной логики. Законы логики. Логические переменные. Логические выражения и их преобразования. Построение таблиц истинности логических выражений

Билет № 8

Алгебра логики — раздел математики, изучающий высказывания, рассматриваемые с точки зрения их логических значений (истинности или ложности) и логических операций над ними.

Под логическим высказыванием понимается любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно. Например, логическим высказыванием будет “Земля — третья планета от Солнца”, но не является таковым “Довольно морозная в этом году зима”.

Чаще на практике приходится иметь дело с высказывательными формами — повествовательными предложениями, прямо или косвенно содержащими переменные; высказывательная форма становится логическим высказыванием, если значения всех переменных, входящих в нее, заданы. Например, высказывательная форма “ x кратно 5” при x = 34 ложна, а при x = 105 — истинна. В языках программирования высказывательные формы записываются в виде логических выражений.

Буквы, обозначающие переменные высказывания, называются высказывательными переменными (логическими переменными).

Простые логические высказывания могут быть объединены в более сложные — составные — с использованием логических операций. Основными логическими операциями являются НЕ (отрицание, или инверсия), И (конъюнкция, или логическое умножение), ИЛИ (дизъюнкция, или логическое сложение).

Рассмотрим более подробно логические операции.

Если для арифметических операций используются таблицы сложения и умножения, задающие правила выполнения этих операций для цифр системы счисления и которые в дальнейшем используются при выполнении сложения и вычитания, умножения и деления соответственно, так и для логических операций строят аналогичные таблицы, называя их таблицами истинности.

Операция инверсии (отрицания) выполняется над одним операндом (так в математике называются величины, над которыми выполняют ту или иную операцию). Общее правило, заложенное в построение таблицы истинности для этой операции, звучит так: отрицаниеизменяетзначениеоперанданапротивоположное.

Обозначение операции: A, .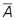

Операция дизъюнкции выполняется над двумя операндами. Общее правило, заложенное в построение таблицы истинности для этой операции, звучит так: дизъюнкцияложнатогдаитолькотогда,когдаложныобаоперанда. В таблице истинности перечисляются все возможные сочетания значений операндов и соответствующие значения операции.

В литературе операцию дизъюнкции обозначают по-разному: ИЛИ, . В языках программирования также имеется эта операция. В Pascal и Вasic она обозначается OR, в С/C++, JavaScript — ||, и т.д.

Логическим сложением эту операцию называют по той причине, что если заменить значение истина на 1, а ложь — на 0, то таблица истинности в определенной мере будет соответствовать таблице сложения в двоичной системе счисления. В действительности роль дизъюнкции в алгебре логики аналогична роли операции сложения в арифметике.

Операция конъюнкции выполняется над двумя операндами. Общее правило, заложенное в построение таблицы истинности для этой операции, звучит так: конъюнкцияистиннатогдаитолькотогда,когдаистинныобаоперанда. В таблице истинности перечисляются все возможные сочетания значений операндов и соответствующие значения операции.

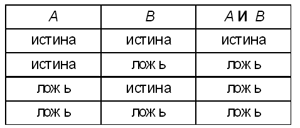
В литературе операцию конъюнкции обозначают по-разному: И, , & (достаточно часто в записи выражений знак конъюнкции пропускают по аналогии со знаком умножения в записи алгебраических выражений). В языках программирования также присутствует эта операция. В Pascal и Basic она обозначается AND, в С/C++, JavaScript — &&, и т.д.

Логическим же умножением эту операцию называют по той причине, что если заменить значение истина на 1, а ложь — на 0, то таблица истинности будет соответствовать таблице умножения в двоичной системе счисления.

Операция следования (импликации) выполняется над двумя операндами. Общее правило, заложенное в построение таблицы истинности для этой операции, звучит так: импликацияложна,еслиизистиныследуетложь,иистиннавовсехостальныхслучаях. В таблице истинности перечисляются все возможные сочетания значений операндов и соответствующие значения операции (обозначается импликация обычно ).

Операция эквивалентности (эквиваленции) выполняется над двумя операндами. Общее правило, заложенное в построение таблицы истинности для этой операции, звучит так: эквиваленцияистиннатогдаитолькотогда,когдаобаоперандапринимаютодинаковыезначения. В таблице истинности перечисляются все возможные сочетания значений операндов и соответствующие значения операции (обозначается эквиваленция обычно ).

Свойства логических операций (или законы логики; знак “ 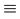” обозначает “эквивалентно”, “тождественно истинно”):

Логические выражения определяют порядок вычисления логического значения. Путем преобразования исходных логических выражений с использованием законов логики можно получать равносильные им более простые выражения. В общем случае равносильность логических выражений определяется совпадением таблиц истинности для этих выражений.

Пример 1. Упростить выражение и убедиться, что результат равносилен исходному выражению.

(в записи выражения знак конъюнкции пропущен).

Преобразование выполним последовательно.

Рассмотрим вторую скобку: . По закону поглощения получаем Y.

В третьей скобке используем закон де Моргана: .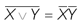

Таким образом, получили . Используя законы коммутативный, противоречия, а также правило , приходим к выводу, что выражение .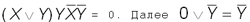

Таким образом, .

Предлагаем читателю самостоятельно, с помощью составления таблиц истинности для исходного и конечного выражений, убедиться в их равносильности.

Пример 2. Доказать, что выражение является тавтологией¹.

Проведем доказательство путем упрощения исходного выражения.

Проведем доказательство путем составления таблицы истинности для данного выражения:

Таким образом, вновь получаем тот же результат: выражение является тавтологией.

Литература

1. Шауцукова Л.З. Информатика: Учебное пособие для 10–11-х классов общеобразовательных учреждений. 2-е изд., дораб. М.: Просвещение, 2002, 416 с.

2. Андреева Е.В. Математические основы информатики. Элективный курс: Учебное пособие / Е.В. Андреева, Л.Л. Босова, И.Н. Фалина. М.: БИНОМ. Лаборатория Знаний, 2005, 328 с.

3. Семакин И., Залогова Л., Русаков С., Шестакова Л. Информатика: учебник по базовому курсу. М.: Лаборатория Базовых Знаний, 1998.

4. Угринович Н. Информатика и информационные технологии. Учебное пособие для общеобразовательных учреждений. М.: БИНОМ, 2001, 464 с. (Введение в информатику, с. 13–16.)

5. http://comp-science.narod.ru.

¹ Тавтология — тождественно истинное выражение.

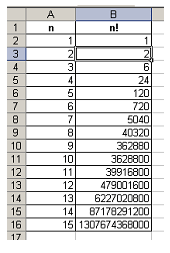
Пример. Получить в электронной таблице первые 15 значений функции n!

Решение. Зададим факториал рекуррентным соотношением: an = an -1• n, a 1 = 1

Пусть столбец A хранит значения n, а столбец
B — n!. Тогда в ячейки A2:A16 занесем значения n от 1 до 15. В ячейку B2 поместим значение 1, а в ячейке B3 запишем формулу =B2 * A3, выражающую записанное рекуррентное соотношение; далее скопируем эту формулу во все последующие ячейки столбца и получим требуемый результат.

Варианты заданий

Получить в электронной таблице первые k значений последовательности (k задается учителем).

.

Пример. Написать программу, исполняющую алгоритм, записанный в виде нижеприведенной блок-схемы. Распечатать значение переменной с.

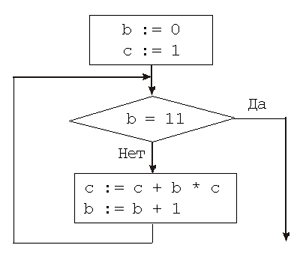
Решение.

Дата добавления: 2015-04-23