Билет № 9.

Pascal

QBasic

B = 0: C = 1

While B <> 11

C = C + B * C

B = B + 1

Wend;

PRINT C

Var b, c: longint;

Begin

B:= 0; C:= 1;

While B <> 11 do

Begin

C:= C + B * C;

B:= B + 1

End;

Writeln(C)

End.

C++

#include <iostream.h>

void main()

{ long B, C;

B = 0; C = 1;

while (B!= 11)

{ C = C + B * C;

B++; }

cout << C;

}

Результат вычислений: 39 916 800.

Вариантызаданий

Написать программу, исполняющую алгоритм, записанный в виде одной из нижеприведенных блок-схем. Выполнить указанное задание.

1. Вывести значение переменной K для n = 12 981.

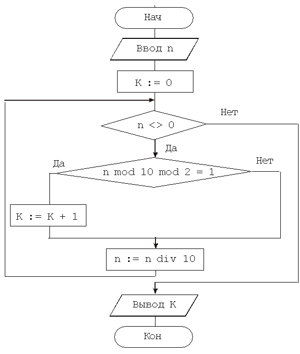
2. Вывести значение переменной P при k = 5.

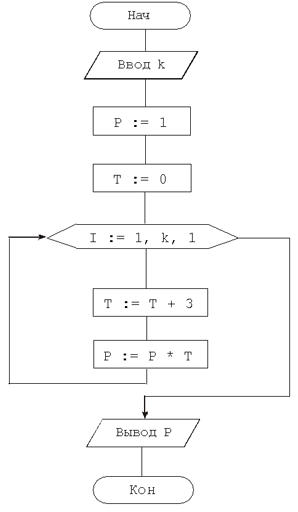
3. Вывести значение переменной K для n = 12 981.

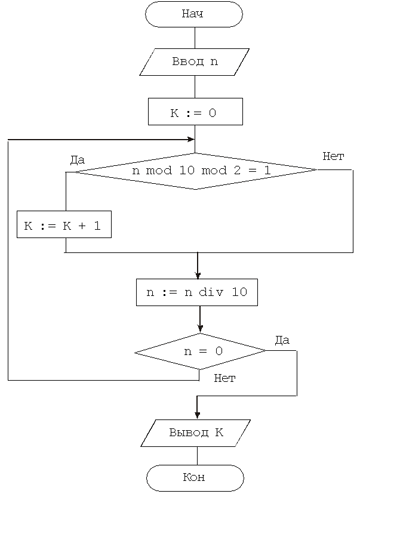
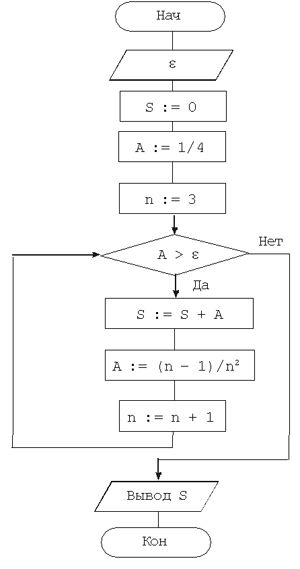
4. Какое количество членов ряда будет просуммировано при e = 10–2?

.

1. Логические элементы и схемы. Типовые логические устройства компьютера: полусумматор, сумматор, триггеры, регистры. Описание архитектуры компьютера с опорой на составляющие ее логические устройства

Обсудив в билете № 8 теоретические аспекты логических функций, сегодня мы поговорим об их практической реализации в виде логических элементов. Следует особо подчеркнуть, что в настоящее время основу всех компьютерных устройств (включая даже встроенные в бытовую технику!) составляют двоичные электронные логические элементы¹. Поэтому понимание базовых идей их функционирования для представления об общей логике работы компьютера весьма полезно.

Может показаться, что для реализации всевозможных логических функций требуется большое разнообразие логических элементов. Как ни удивительно, но это не так. Из теории логических функций следует, что достаточно их очень небольшого базового набора, чтобы с помощью различных комбинаций, его составляющих, можно было получить абсолютно произвольную функцию, сколь бы сложной она не была. Следовательно, и количество базовых логических элементов, которые соответствуют данным функциям, к счастью, невелико. Базисный набор может быть сформирован различными способами, но, как правило, используется классическая “тройка” логических операций И, ИЛИ, НЕ. Именно эта “тройка” применяется в книгах по логике, а также во всех языках программирования — от машинных кодов до языков высокого уровня. Обозначения логических элементов², реализующих соответствующие операции, приведены на рис. 1 a–b.

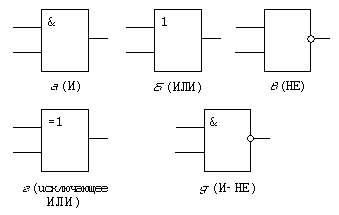
Рис. 1. Обозначения основных логических элементов

Внутренняя схема логического элемента может быть различной, более того, она может существенно совершенствоваться по мере развития технологий производства, но логические функции всегда остаются неизменными.

Часто для удобства синтеза логических схем к перечисленному списку добавляют еще элемент “исключающее ИЛИ” (рис. 1 г), который позволяет сравнивать двоичные коды на совпадение. Данная операция имеет и другие практически полезные свойства, в частности, восстанавливает исходные данные в случае повторного применения, что удобно использовать для временного наложения видеоизображений.

Тем не менее классический базис не является единственным. Более того, для практической реализации логических схем инженеры предпочитают альтернативный вариант — на базе единственного комбинированного логического элемента И-НЕ (рис. 1 д). Читатели, которые заинтересовались данным вопросом, могут обратиться к книге Р.Токхейма [2] или аналогичной, где показано, как из элементов И-НЕ можно построить все остальные примитивы классического базиса.

Отметим, что на практике логические элементы могут иметь не только два, но и значительно большее количество входов (для примера см. рис. 4 на с. 24).

Первоначально тезис о построении любых логических устройств на основе некоторого простого базиса был технически реализован “один к одному”: были разработаны и выпускались интегральные микросхемы (ИМС), соответствующие основным логическим действиям. Потребитель, комбинируя имеющиеся в его распоряжении элементы, мог получить схему с реализацией любой необходимой логики. Довольно быстро стало ясно, что подобное “строительство здания из отдельных кирпичиков” слишком трудоемко и не может удовлетворить постоянно растущие практические потребности. Промышленность увеличила степень интеграции микросхем и начала выпускать более сложные типовые узлы: триггеры, регистры, счетчики, дешифраторы, сумматоры и т.д. (продолжая аналогию со строительством, этот шаг, видимо, следует уподобить панельному способу домостроения). Новые микросхемы давали возможность реализовывать еще более сложные электронные логические устройства, но зато ассортимент выпускаемых микросхем расширился. Поскольку человечеству свойственно не останавливаться на достигнутом, рост возможностей породил новые потребности. Необходимым образом последовал переход к большим интегральным схемам (БИС), представлявшим собой функционально законченные узлы, а не отдельные компоненты для их создания (как тут не вспомнить блочный метод постройки здания из готовых комнат). Наконец, дальнейшая эволюция технологий производства ИМС привела к настолько высокой степени интеграции, что в одной БИС содержалось функционально законченное изделие: часы, калькулятор, небольшая специализированная ЭВМ.

Примечание. Немногие, вероятно, знают, что появление первых микропроцессоров было связано вовсе не с попытками воспроизвести ЭВМ в одном кристалле: действительной причиной явилось стремление существенно ограничить ассортимент логических микросхем, повышая их универсальность и, как следствие, понижая стоимость за счет резкого роста объемов производства. Весьма поучительная история о замене дюжины специализированных микросхем одной программируемой, что, собственно, и привело к созданию инженером М.Хоффом первого микропроцессора Intel 4004, рассказывается в книге
А.П. Частикова [3].

Если мы посмотрим на внутреннее устройство типичного современного компьютера, то увидим там ИМС очень высокого уровня интеграции: микропроцессор, модули ОЗУ, контроллеры внешних устройств и др. Фактически каждая микросхема или небольшая группа микросхем³ образует функционально законченный блок. Уровень сложности блока таков, что разобраться в его внутреннем устройстве для неспециалиста не то чтобы нецелесообразно, а просто невозможно. К тому же выпускаемые промышленностью ИМС постоянно совершенствуются и усложняются. В результате оказывается, что для понимания наиболее общих принципов работы современной ЭВМ удобнее и правильнее рассмотреть несколько типовых узлов, а изучение поведения отдельных БИС заменить изучением функциональной схемы компьютера.

В качестве характерных цифровых устройств мы выберем два наиболее важных и интересных — сумматор и триггер. Первое из них замечательно тем, что составляет основу арифметико-логического устройства процессора, а второе, будучи универсальным устройством для хранения одного бита информации, имеет еще более широкое применение — от регистров процессора до элементов памяти. Дополнительно подчеркнем, что выбранные логические схемы принадлежат к разным типам. Выходные сигналы сумматора определяются исключительно установившимися на входе напряжениями и никак не зависят от поступавших ранее сигналов (в литературе такие схемы часто называют комбинационными). Состояние триггера, напротив, зависит от предыстории, т.е. схема имеет память.

Перейдем к описанию логической схемы сумматора. Для простоты ограничимся изучением работы отдельного двоичного разряда. В этом случае сумматор будет содержать три входа — бит первого слагаемого А, второго — В и перенос из предыдущего разряда Ci (обозначение происходит от английских слов Carry in — входной перенос). Тем, для кого термин перенос звучит незнакомо, уместно вспомнить, что означает словосочетание “ноль пишем один в уме”, которое они часто повторяли про себя, суммируя в младших классах числа на листке бумаги.

Таблица истинности для полного одноразрядного сумматора имеет вид:

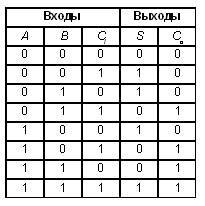
Особых комментариев к этой таблице не требуется. Может быть, только стоит напомнить тот факт, что 1 + 1 = 0 и 1 “в уме” (т.е. на выходе C o, что расшифровывается как Carry out, т.е. выходной перенос), поскольку все действия выполняются в двоичной системе.

Построить сразу полный сумматор — задача для начинающего непростая. Она еще более усложняется, если при этом требуется использовать логические элементы из реально существующего ассортимента интегральных микросхем. Вариант схемы сумматора, приведенный, например, в книгах [4] и [5], состоит из 9 логических элементов. Минимизированная схема, полученная в [6], построена на базе 6 классических элементов. К счастью, для понимания принципов работы суммирующих схем ЭВМ существует еще более простое решение, если воспользоваться логическими элементами “исключающее ИЛИ” [7].

При построении схемы удобно сумматор представить в виде двух полусумматоров, из которых первый складывает разряды А и В, а второй к полученному результату прибавляет бит переноса из предыдущего разряда Ci.

Таблица истинности для полусумматора значительно упрощается:

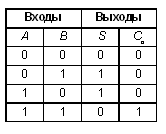
Теперь мысленно объединим в приведенной таблице столбцы A, B и C o. Что напоминает вам полученная таблица? Конечно же базовый логический элемент И! Аналогично, сравнив первые три столбца A, B и S с таблицей истинности для элемента “исключающее ИЛИ”, можно убедиться, что они совпадут (рекомендуем читателям самостоятельно убедиться в этом, а также проверить тот факт, что сумма S равна 1 только в случае несовпадения исходных битов). Таким образом, для реализации полусумматора достаточно соединить параллельно входы двух логических элементов (см. рис. 2 a)!

Рис. 2. Простейшая реализация сумматора

Заметим, что для суммирования младшего разряда одного полусумматора уже достаточно, т.к. в этом случае сигнал входного переноса отсутствует. А если соединить два полусумматора, как показано на рис. 2 б, то получится полный сумматор, способный осуществить сложение одного бита чисел с учетом возможности переноса.

Перейти к многоразрядным числам можно, например, путем последовательного соединения соответствующего количества сумматоров. Мы не будем обсуждать возникающие при этом детали, связанные с необходимостью ускорения процесса переноса в такой схеме; думается, мы уже изучили вполне достаточно, чтобы иметь некоторое представление о том, как компьютер производит свои вычисления.

Стоит особо подчеркнуть, что сумматор играет важную роль в реализации не только сложения, но и других арифметических действий. Например, вычитание обычно заменяется сложением с дополнительным кодом вычитаемого, а алгоритм умножения “столбиком” легко сводится к комбинации сложений и сдвигов. Таким образом, сумматор необходимой разрядности фактически является основой арифметического устройства современного компьютера.

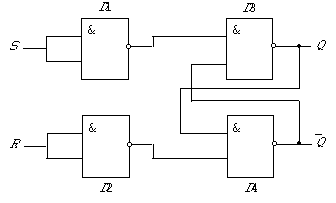
Рис. 3. Схема RS -триггера

Перейдем теперь к описанию работы триггера. Его схема приведена на рис. 3, а таблица истинности имеет следующий вид:

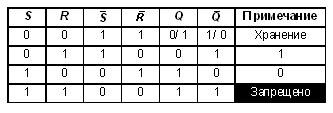
Как видно из рис. 3, триггер собран из четырех логических элементов И-НЕ, причем два из них играют вспомогательную роль инверторов входных сигналов. Триггер имеет два входа, обозначенные на схеме R и S, а также два выхода, помеченные буквой Q, — прямой и инверсный (черта над Q у инверсного выхода означает отрицание). Триггер устроен таким образом, что на прямом и инверсном выходах сигналы всегда противоположны.

Как работает триггер? Пусть на входе R установлена 1, а на S — 0. Логические элементы D 1 и D 2 инвертируют эти сигналы, т.е. меняют их значения на противоположные; в результате на вход элемента D 3 поступает 1, а на D 4 — 0. Поскольку на одном из входов D 4 имеется 0, независимо от состояния другого входа на его выходе (он же является инверсным выходом триггера!) обязательно установится 1. Эта единица передается на вход элемента D 3 и в сочетании с 1 на другом входе порождает на выходе D 3 логический 0. Итак, при R = 1 и S = 0 на прямом выходе триггера устанавливается 0, а на инверсном — 1.

Обозначение состояния триггера по договоренности связывается с прямым выходом. Тогда при описанной выше комбинации входных сигналов результирующее состояние можно условно назвать нулевым: говорят, что триггер устанавливается в 0 или сбрасывается. Сброс по-английски называется Reset, отсюда вход, появление сигнала на котором приводит к сбросу триггера, принято обозначать буквой R.

Проведите аналогичные рассуждения для “симметричного” случая R = 0 и S = 1. Вы увидите, что теперь, наоборот, на прямом выходе получится логическая 1, а на инверсном — 0. Триггер перейдет в единичное состояние — установится (установка по-английски Set).

Далее рассмотрим наиболее распространенную и интересную ситуацию R = 0 и S = 0, когда входных сигналов нет. Тогда на входы элементов D 3 и D 4, связанные с R и S, будет подана 1, и их выходной сигнал будет зависеть от напряжения на других входах. Нетрудно убедиться, что такое состояние будет устойчивым. Пусть, например, на прямом выходе была 1. Тогда наличие единиц на обоих входах элемента D 4 “подтверждает” нулевой сигнал на его выходе. В свою очередь, наличие 0 на инверсном выходе передается на D 3 и поддерживает его выходное единичное состояние. Аналогично доказывается устойчивость картины и для противоположного состояния триггера, когда Q = 0.

Таким образом, при отсутствии входных сигналов триггер сохраняет свое “предыдущее” состояние. Иными словами, если на вход R подать 1, а затем убрать, триггер установится в нулевое состояние и будет его сохранять, пока не поступит сигнал на другой вход S. В последнем случае он перебросится в единичное состояние и после прекращения действия входного сигнала будет сохранять на прямом выходе 1. Мы видим, что триггер обладает замечательным свойством: после снятия входных сигналов он сохраняет свое состояние, а значит, может служить устройством для хранения одного бита информации.

В заключение проанализируем последнюю комбинацию входных сигналов R = 1 и S = 1. Нетрудно убедиться (проделайте необходимые рассуждения самостоятельно), что в этом случае на обоих выходах триггера установится 1! Такое состояние, помимо своей логической абсурдности, еще и является неустойчивым: после снятия входных сигналов триггер случайным образом перейдет в одно из своих устойчивых состояний. Вследствие этого комбинация R = 1 и S = 1 на практике не используется и является запрещенной.

Мы рассмотрели простейший RS -триггер. Существуют и другие разновидности этого интересного и полезного устройства. Все они различаются не столько принципом работы, сколько входной логикой, усложняющей “поведение” триггера.

Подобно тому, как объединяются для обработки двоичных чисел однобитовые схемы сумматоров, для хранения многоразрядных данных триггеры объединяются в единый блок, называемый регистром. Над регистром, как над единым целым, можно производить ряд стандартных операций: сбрасывать (обнулять), заносить в него код и некоторые другие. Причем часто регистры способны не просто хранить информацию, но и обрабатывать ее. Типичными примерами такого типа могут служить регистр, который способен сдвигать находящийся в нем двоичный код, или регистр, подсчитывающий количество поступающих импульсов, — счетчик.

С выходов триггеров регистра сигналы могут поступать на другие цифровые устройства. Особый интерес с точки зрения принципов функционирования компьютера представляет схема анализа равенства (или неравенства) регистра нулю, которая позволяет организовать по этому признаку условный переход. Для n -разрядного двоичного регистра потребуется n -входовый элемент И⁴ (см. рис. 4), сигналы для которого удобнее снимать с инверсных выходов триггеров. Фактически такая схема анализа выполняет комбинированную логическую операцию НЕ-И.

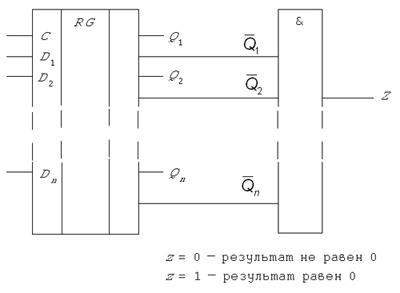
Рис. 4. Схема анализа состояния регистра

В самом деле, пусть содержимое всех битов регистра равно 0. Тогда на вход элемента И с инверсных выходов триггеров поступают все 1 и результат z = 1. Если же хотя бы один из разрядов отличен от 0, то с его инверсного выхода снимается 0 и этого, как известно, уже достаточно, чтобы получить выходной сигнал z = 0 независимо от состояния всех остальных входов элемента И.

Таким образом, изображенная на рис. 4 логическая схема вырабатывает управляющий сигнал равенства результата 0, что может использоваться, например, для организации ветвления по соответствующему условию. Кстати, переход по знаку числа реализовать еще проще — достаточно проанализировать состояние знакового (обычно старшего) разряда: если он установлен в 1, то регистр содержит отрицательное число [5].

Наличие управляющих признаков, устанавливаемых в зависимости от полученного результата операции, является неотъемлемым свойством процессоров. Оно необходимо для организации выполнения инструкций ветвления и цикла⁵.

Триггеры очень широко применяются в компьютерной технике. Помимо уже описанного применения в составе разнообразных регистров, на их основе могут еще изготовляться быстродействующие ИМС статического ОЗУ (в том числе кэш-память). Так что в состав любого микропроцессора входит множество триггеров, выполняющих самые разнообразные функции.

Мы с вами изучили только два из многочисленных устройств вычислительной техники — сумматор и регистры. Казалось бы, много ли можно понять, зная всего два этих устройства? Оказывается, не так уж и мало. Можно, например, весьма успешно попытаться представить себе, как строится арифметическое устройство процессора. В самом деле, подумаем, каким образом можно спроектировать схему для реализации сложения двух чисел. Очевидно, что для хранения исходных чисел потребуется два триггерных регистра. Их выходы подадим на входы сумматора, так что на выходах последнего сформируются сигналы, соответствующие двоичному коду суммы. Для фиксации (запоминания) результирующего числа потребуется еще один регистр, который можно снабдить описанными выше схемами формирования управляющих признаков. Наша картина получается настолько естественной и реалистичной, что мы можем найти ее в наиболее подробной учебной литературе в качестве основы устройства простых учебных моделей компьютера. В частности, очень похоже выглядит описание внутреннего устройства процессора учебного компьютера “Нейман”, которое дано в книгах [8, 9]⁶.

Подводя итоги, подчеркнем, что в процессе рассмотрения материала билета мы прошли путь от изучения простейшего единичного логического элемента до понимания наиболее общих идей построения весьма крупных узлов ЭВМ, таких, как арифметическое устройство. Следующий уровень знакомства с логикой работы компьютера — на уровне функциональных устройств (процессор, память и устройства ввода/вывода), будет подробно изложен в билете № 12.

Примечание. Очевидно, что материал, который включается в экзаменационные билеты, имеет существенную значимость для изучаемого учебного предмета. В связи с этим автору данных строк особо хотелось бы подчеркнуть важность темы с точки зрения формирования у учеников некоторого единого представления об устройстве компьютера. Мировоззрение складывается не только (а может, даже и не столько) в ходе рассуждений “о высоких материях”, но и в результате создания некоторой единой связной картины изучаемого материала. Очень важно, чтобы темы отдельных уроков не казались независимыми, выбранными по странной прихоти какого-то неведомого теоретика. В этом смысле значение вопроса, соединяющего отдельные логические элементы с узлами реального вычислительного устройства, трудно переоценить. Иными словами, ценность материала заключается в том, что он “перекидывает мостик” между разрозненными абстрактными знаниями о логических элементах и архитектурой реального компьютера. В школьной практике это служит надежным средством борьбы с традиционным “Зачем все это нужно?”.

Литература

1. Ямпольский В.С. Основы автоматики и электронно-вычислительной техники: Учебное пособие для студентов физико-математического факультета педагогических институтов. М.: Просвещение, 1991, 223 с.

2. Токхейм Р. Основы цифровой электроники. М.: Мир, 1988, 392.

3. Частиков А.П. История компьютера. М.: Информатика и образование, 1996, 128 с.

4. Касаткин В.Н. Информация, алгоритмы, ЭВМ: Пособие для учителя. М.: Просвещение, 1991, 192 с.

5. Андреева Е.В., Босова Л.Л., Фалина И.Н. Математические основы информатики. Элективный курс. М.: БИНОМ. Лаборатория Знаний, 2005, 328 с.

6. Акулов О.А., Медведев Н.В. Информатика: базовый курс: Учебное пособие для студентов вузов. М.: Омега-Л, 2005, 552 с.

7. Кушниренко А.Г., Лебедев Г.В., Зайдельман Я.Н. Информатика, 7–9-е классы: Учебник для общеобразовательных учебных заведений. М.: Дрофа, 2000, 336 с.

8. Основы информатики и вычислительной техники в базовой школе / Л.А. Залогова, С.В. Русаков, И.Г. Семакин, Е.К. Хеннер, Л.В. Шестакова; под ред. И.Г. Семакина. Пермь, 1995.

9. Семакин И.Г. Информатика. Беседы об информации, компьютерах и программах: Книга для учащихся 8–9-х классов. Часть 2. Пермь: Изд-во Пермского университета, 1997, 168 с.

10. Информатика в понятиях и терминах: Книга для учащихся старших классов средней школы /
Г.А. Бордовский, В.А. Извозчиков, Ю.В. Исаев,
В.В. Морозов. Под ред. В.А. Извозчикова. М.: Просвещение, 1991, 208 с.

11. Шауцукова Л.З. Информатика: Учебное пособие для 10–11-х классов общеобразовательных учреждений. М.: Просвещение, 2003, 416 с.

Дата добавления: 2015-04-23