Уравнение абсолютных и относительных погрешностей

Связь параметров поля допуска и числовых характеристик случайных величин.

Параметры поля допуска.

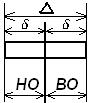
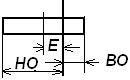
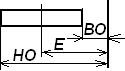
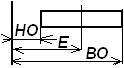
Е – середина поля допуска; 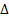- полное поле допуска; 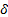- половина поля допуска; НО – нижнее отклонение; ВО – верхнее отклонение.

, , , ,

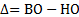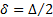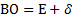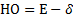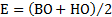
Любое случайное отклонение может быть описано параметрами поля допуска: Е – середина поля допуска; 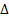- полное поле допуска; 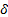- половина поля допуска; НО – нижнее отклонение; ВО – верхнее отклонение.

Рассмотрим относительную погрешность i-го параметра 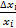, сто случайная величина и она имеет закон распределения .

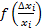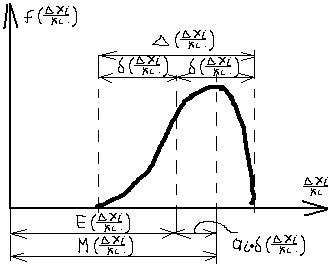
ai – коэффициент относительной асимметрии.

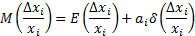
Характеристики разброса случайной величины: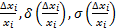

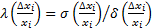- относительное среднее квадратичное отклонение.

Уравнение погрешности связывает отклонение выходного параметра у с отклонениями параметров ЭРЭ и схемных параметров.

Уравнение абсолютных погрешностей.

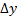– относительная погрешность выходных параметра; 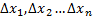- абсолютная погрешность параметров ЭРЭ и схемных параметров.

Для вывода соотношения между 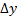и 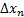рассмотрим частный случай зависимости 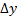от одного параметра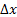

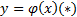
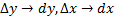
Разложим правую часть уравнения в ряд Тейлора

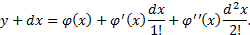
Отбросив в данном уравнении величины 2-го и более высоких порядков из-за их значений получим

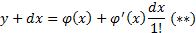
Вычтем из (**) (*), получим

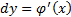
Перейдем к конечным приращениям

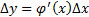
Поскольку в уравнении 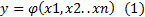параметры 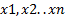независимы, то можем переписать (1) в следующем виде, учтя n параметров:

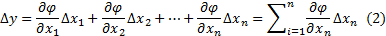
Уравнение (2) – уравнение абсолютных погрешностей. Недостатком данного уравнения является то, что абсолютные погрешности размерны и использовать такое уравнении возможно только в частном случае, когда параметры 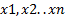имеют одинаковые размерности.

Уравнение относительных погрешностей

Для получения уравнения относительных погрешностей выполним следующую операцию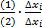

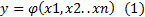
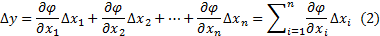
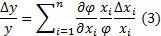
Полученное уравнение (3) относительных погрешностей связывает относительную погрешность выходного параметра и относительную погрешность параметров ЭРЭ и схемных параметров. Относительные погрешности безразмерны, поэтому уравнение 3 можно использовать в случаях, когда выходной параметр зависит от самых разнообразных параметров ЭРЭ и схемных параметров.

Уравнение относительных погрешностей с числовыми коэффициентами.

Запишем уравнение относительных погрешностей в следующем виде: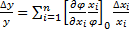

Введем обозначение 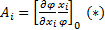и назовем его коэффициентом влияния i-го параметра, он показывает степень влияния относительной погрешности i-го параметра на относительную погрешность выходного параметра .

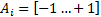Коэффициенты влияния могут быть получены путем расчета, путем проведения эксперимента.

Индекс «0» в соотношении (*) свидетельствует о том, что параметры ЭРЭ и схемные параметры подставляются в виде номинальных значений, параметры активных ЭРЭ в виде параметров рабочей точки.

Порядок расчета: 1) 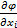2) умножить на 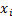3) поделить на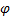

Тогда уравнение относительных погрешностей может быть переписано в виде:

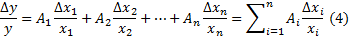
(4) – уравнение относительных погрешностей с числовыми коэффициентами.

Все погрешности (относительные, абсолютные) 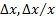параметров ЭРЭ и схемных параметров являются величинами случайными. Поскольку 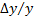является суммой случайных величин, то и 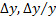тоже случайные величины. Уравнения (1) и (2) являются уравнениями случайных величин.

Поскольку любая случайная величина не обладает никакой отличной от 0 вероятностью, то подставлять в уравнения (2) и (4) конкретные значения отклонений недопустимо.

Дата добавления: 2015-04-23