Условие плавания тел

Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести 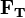и силы Архимеда 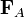, которые действуют на это тело. Возможны следующие три случая:

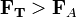§ — тело тонет;

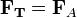§ — тело плавает в жидкости или газе;

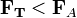§ — тело всплывает до тех пор, пока не начнет плавать.

Другая формулировка (где 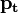— плотность тела, 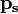— плотность среды, в которую оно погружено):

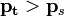§ — тело тонет;

§ — тело плавает в жидкости или газе;

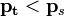§ — тело всплывает до тех пор, пока не начнет плавать.

2. Тонкая линза. Линза (нем. Linse, от лат. lens — чечевица) — деталь из оптически (и не только, линзы также применяются в СВЧ технике, и там обычно состоят из непрозрачных диэлектриков или набора металлических пластин) прозрачного однородного материала, ограниченная двумя полированными преломляющими поверхностями вращения, например, сферическими или плоской и сферической. В настоящее время всё чаще применяются и «асферические линзы», форма поверхности которых отличается от сферы. В качестве материала линз обычно используются оптические материалы, такие как стекло, оптическое стекло, оптически прозрачные пластмассы и другие материалы.

Линза, для которой толщина принята равной нулю, в оптике называется «тонкой».

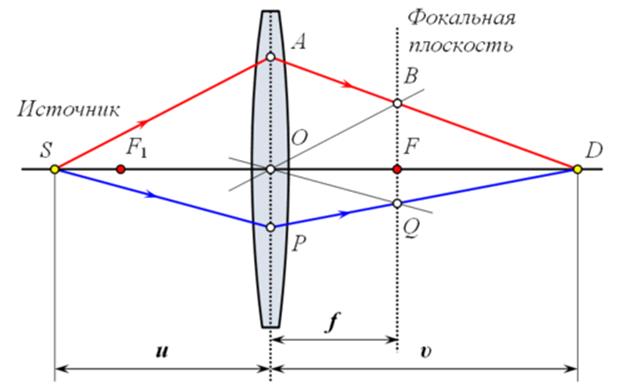
При изложении характеристики линз был рассмотрен принцип построения изображения светящейся точки в фокусе линзы. Лучи, падающие на линзу слева, проходят через её задний фокус, а падающие справа — через передний фокус. Следует учесть, что у рассеивающих линз, наоборот, задний фокус расположен спереди линзы, а передний позади.

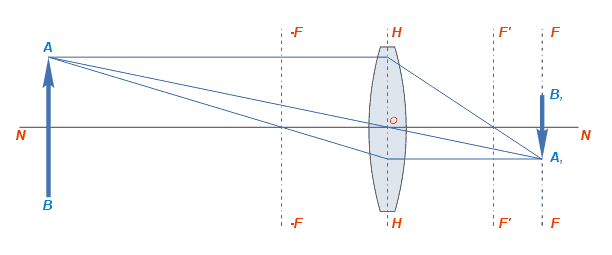
Величина 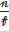называется оптической силой линзы. Оптическая сила линзы измеряется в диоптриях, единицами, измерения которых являются м−1. 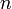— коэффициент преломления материала линзы, 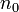- коэффициент преломления среды, окружающей линзу, 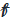– фокусное расстояние.

Билет 23

1. Ламинарное и турбулентное течение жидкостей. Ламинарное течение (лат. lāmina — «пластинка») — течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть беспорядочных быстрых изменений скорости и давления). Ламинарное течение возможно только до некоторого критического значения числа Рейнольдса, после которого оно переходит в турбулентное. Критическое значение числа Рейнольдса зависит от конкретного вида течения (течение в круглой трубе, обтекание шара и т. п.). Например, для течения в круглой трубе 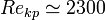. Турбулентность, устар. турбуленция (от лат. turbulentus — бурный, беспорядочный), турбулентное течение — явление, заключающееся в том, что при увеличении скорости течения жидкости или газа в среде самопроизвольно образуются многочисленные нелинейные фрактальные волны и обычные, линейные различных размеров, без наличия внешних, случайных, возмущающих среду сил и/или при их присутствии. Для расчёта подобных течений были созданы различные модели турбулентности. Волны появляются случайно. То есть их размер и амплитуда меняется хаотически в некотором интервале. Они возникают чаще всего либо на границе, у стенки, и/или при разрушении или опрокидывании волны. Они могут образоваться на струях. Экспериментально ее можно наблюдать на конце струи пара из электрочайника. Турбулентность экспериментально открыта английским инженером Рейнольдсом в 1883 году при изучении течения несжимаемой жидкости (воды) в трубах. В гидродинамике уравнение непрерывности называют уравнением неразрывности. Оно выражает собой закон сохранения массы в элементарном объеме, то есть непрерывность потока жидкости или газа. Его дифференциальная форма

,

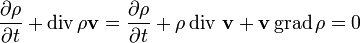где 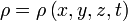— плотность жидкости (или газа), 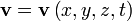— вектор скорости жидкости (или газа) в точке с координатами 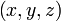в момент времени .

Вектор 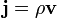называют плотностью потока жидкости. Его направление совпадает с направлением течения жидкости, а абсолютная величина определяет количество вещества, протекающего в единицу времени через единицу площади, расположенную перпендикулярно вектору скорости.

Для несжимаемых жидкостей 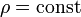. Поэтому уравнение принимает вид

,

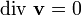из чего следует соленоидальность поля скорости. Давление жидкости, текущей по трубе, меньше там, где скорость её течения больше, и, наоборот, где скорость течения жидкости меньше, давление там больше. Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

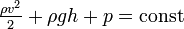
Здесь

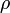— плотность жидкости,

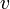— скорость потока,

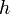— высота, на которой находится рассматриваемый элемент жидкости,

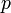— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,

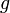— ускорение свободного падения.

Константа в правой части обычно называется напором, или полным давлением, а также интегралом Бернулли. Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости.

Это соотношение, выведенное Даниилом Бернулли в 1738 г., было названо в его честь уравнением Бернулли (не следует путать с дифференциальным уравнением Бернулли).

Для горизонтальной трубы 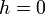и уравнение Бернулли принимает вид: .

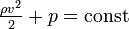Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности : .

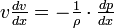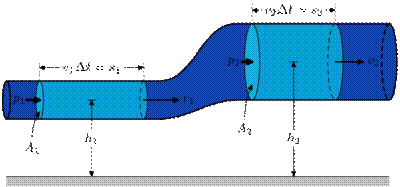
Согласно закону Бернулли, полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока.

В газе также выполняется этот закон при скоростях его движения менее v ≈ 340 м/с - скорости звука: пульверизатор, крыло (циркуляция потока вокруг крыла).

V_П
p_В < p_H - возникает подъёмная сила

В реальных жидкостях и газах возникает внутреннее трение слоёв - вязкость, которая понижается с повышением температуры для жидкостей и возрастает для газов. Сила трения за счёт вязкости для двух плоскопараллельных пластин равна

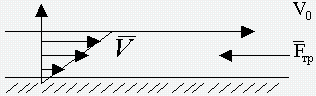где v скорость движения пластинки, S - площадь, d - расстояние между ними, η - коэффициент вязкости. Скорость перемещения слоёв меняется как
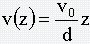, т.е. - сила трения для слоёв жидкости, соприкасающихся между собой.

В трубе скорость жидкости равна нулю около стенок и меняется к центру по закону

На единицу (S=1) поверхности (цилиндрической) действует сила трения (по модулю).

Пуазейль в 1841 г. установил, что средняя скорость ламинарного течения жидкости в трубе равна
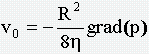- закон Пуазейля,
где 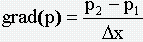. Тогда объём жидкости, протекающей в трубе, равен

.

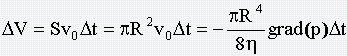При движении тел в жидкостях и газах на них действуют сила лобового сопротивления и подъёмная сила. В идеальной жидкости сила лобового сопротивления отсутствует из-за ламинарности обтекания для бесконечного цилиндра - симметричная картина. Реально за телом всегда возникает турбулентность из-за отрыва слоя. Энергия вихрей расходуется на нагрев жидкости, давление сзади будет ниже, чем спереди возникает сила сопротивления.

Для шарика сила сопротивления равна

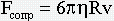
- закон Стокса.
F_сопр минимальна для тел каплевидной формы.

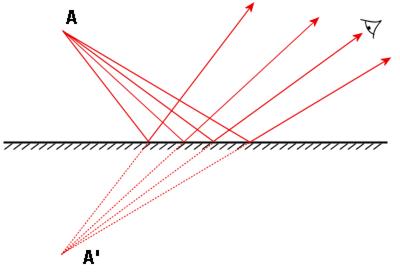
2. Плоское зеркало. Принцип хода лучей, отражённых от зеркала прост, если применять законы геометрической оптики, не учитывая волновую природу света. Луч света падает на зеркальную поверхность (рассматриваем полностью непрозрачное зеркало) под углом альфа к нормали (перпендикуляру), проведённой к точке падения луча на зеркало. Угол луча отражённого будет равен тому же значению-альфа. Луч, падающий на зеркало под прямым углом к плоскости зеркала, отразится сам в себя.

Для простейшего — плоского — зеркала изображение будет расположено за зеркалом симметрично предмету относительно плоскости зеркала, оно будет мнимым, прямым и такого же размера, как сам предмет. Это нетрудно установить, пользуясь законом отражения света[1]. Плоское зеркало также можно рассматривать как предельный случай сферического зеркала (неважно, выпуклого, или вогнутого), при радиусе стремящемся к бесконечности, тогда его свойства получаются из формулы сферического зеркала и формулы увеличения сферического зеркала. Изображение A' точечного источника света A в плоском зеркале.:

Билет 24

1. Импульс точки. И́мпульс (Количество движения) — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:

.

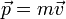В более общем виде, справедливом также и в релятивистской механике, определение имеет вид:

Импульс — это аддитивный интеграл движения механической системы, связанный согласно теореме Нётер с фундаментальной симметрией — однородностью пространства.

В классической механике полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости:

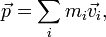
соответственно величина 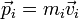называется импульсом одной материальной точки. Это векторная величина, направленная в ту же сторону, что и скорость частицы. Единицей измерения импульса в Международной системе единиц (СИ) является килограмм-метр в секунду (кг·м/с).

Отношение изменения импульса системы к изменению времени равняется сумме всех внешних сил. Это и есть одна из формулировок закона изменения импульса. Классическая формулировка гласит: скорость изменения полного импульса системы равна векторной сумме внешних сил, действующих на систему.

Импульс силы — это векторная физическая величина, равная произведению силы на время её действия, мера воздействия силы на тело за данный промежуток времени (в поступательном движении).

За конечный промежуток времени эта величина равна определённому интегралу от элемен­тарного импульса силы, где пределами интегрирования являются моменты начала и конца промежутка времени действия силы. В случае одновременного действия нескольких сил сумма их импульсов равна импульсу их равнодействующей за то же время.

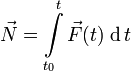
Во вращательном движении момент силы, действуя в течение определённого времени, создаёт импульс момента силы. Импульс момента силы — это мера воздействия момента силы относительно данной оси за данный промежуток времени (во вра­щательном движении):

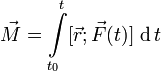
где — векторное произведение.

Формулировка второго закона Ньютона с использованием понятия импульса:

В инерциальной системе отсчета производная импульса материальной точки по времени равна действующей на него силе.

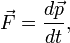
где 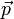— импульс (количество движения) тела, — время, а 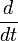— производная по времени.

P.S. Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

2. Рассеивающая линза. Лучи, падающие на рассеивающую линзу, по выходе из неё будут преломляться в сторону краёв линзы, то есть рассеиваться. Если эти лучи продолжить в обратном направлении так, как показано на рисунке пунктирной линией, то они сойдутся в одной точке F, которая и будет фокусом этой линзы. Этот фокус будет мнимым.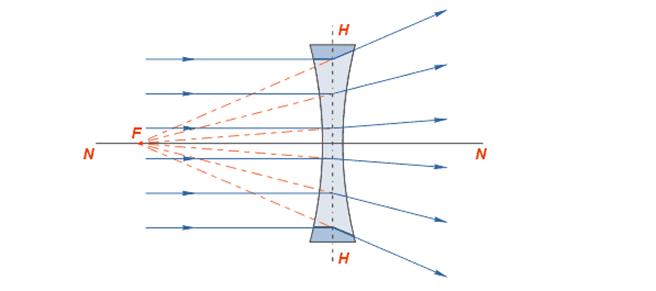

Формула тонкой линзы

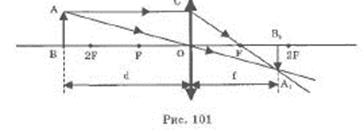
Формула тонкой линзы связывает d (расстояние от предмета до оптического центра линзы), f (расстояние от оптического центра до изображения) с фокусным расстоянием F (рис. 101).

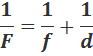
Это и есть формула тонкой линзы.

Расстояния F, d и f от линзы до действительных точек берутся со знаком плюс, расстояния от линзы до мнимых точек - со знаком минус.

Отношение размера изображения Н к линейному размеру предмета h называют линейным увеличением линзы Г.

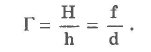
Дата добавления: 2015-04-23