
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные компоненты
|
|
|
|
Основными компонентами информационной технологии, используемой в экспертной системе, являются: интерфейс пользователя, база знаний, интерпретатор, модуль создания системы.

30. Классификация математических моделей в экономике.
Существует значительное разнообразие видов, типов экономико-математических моделей, необходимых для использования в управлении экономическими объектами и процессами. Экономико-математические модели подразделяются на макроэкономические и микроэкономические в зависимости от уровня моделируемого объекта управления, динамические, которые характеризуют изменения объекта управления во времени, и статические, которые описывают взаимосвязи между разными параметрами, показателями объекта именно в то время. Дискретные модели отображают состояние объекта управления в отдельные, фиксированные моменты времени. Имитационными называют экономико-математические модели, используемые с целью имитации управляемых экономических объектов и процессов с применением средств информационной и вычислительной техники. По типу математического аппарата, применяемого в моделях, выделяются экономико-статистические, модели линейного и нелинейного программирования, матричные модели, сетевые модели.
Факторные модели. В группу экономико-математических факторных моделей входят модели, которые с одной стороны включают экономические факторы, от которых зависит состояние управляемого экономического объекта, а с другой - зависимые от этих факторов параметры состояния объекта. Если факторы известны, то модель позволяет определить искомые параметры. Факторные модели чаще всего предоставлены простыми в математическом отношении линейными или статическими функциями, которые характеризуют связь между факторами и зависимыми от них параметрами экономического объекта.
|
|
|
Балансовые модели. Балансовые модели как статистические, так и динамические широко применяются в экономико-математическом моделировании. В основе создания этих моделей лежит балансовый метод - метод взаимного сопоставления материальных, трудовых и финансовых ресурсов и потребностей в них. Описывая экономическую систему в целом, под её балансовой моделью понимают систему уравнений, каждое из которых выражает потребность баланса между изготовленными отдельными экономическими объектами количества продукции и совокупной потребностью в этой продукции. При таком подходе экономическая система состоит из экономических объектов, каждый из которых выпускает некоторый продукт. Если вместо понятия «продукт» ввести понятие «ресурс», то под балансовой моделью необходимо понимать систему уравнений, которые удовлетворяют требования между определенным ресурсом и его использованием.
Наиболее важные виды балансовых моделей:
· Материальные, трудовые и финансовые балансы для экономики в целом и отдельных ее отраслей;
· Межотраслевые балансы;
· Матричные балансы предприятий и фирм.
Оптимизационные модели. Большой класс экономико-математических моделей образуют оптимизационные модели, которые позволяют выбрать из всех решений наилучший оптимальный вариант. В математическом содержании оптимальность понимается как достижение экстремума критерия оптимальности, называемой также целевой функцией. Оптимизационные модели чаще всего используются в задачах нахождения лучшего способа использования экономических ресурсов, что позволяет достичь максимального целевого эффекта. Математическое программирование образовалось на основе решения задачи про оптимальный раскрой листов фанеры, что обеспечивает наиболее полное использование материала. Поставив такую задачу, известный российский математик и экономист академик Л.В.Канторович был признан достойным Нобелевской премии в экономике.
|
|
|
31. Основные этапы построения моделей.
Сущность построения математической модели состоит в том, что реальная система упрощается, схематизируется и описывается с помощью того или иного математического аппарата. Выделяют следующие основные этапы построения моделей.
1. Содержательное описание моделируемого объекта. Словесно описывается объект моделирования, цели его функционирования, среда, в которой он функционирует, выявляются отдельные элементы, возможные состояния, характеристики объекта и его элементов, определяются взаимосвязи между элементами, состояниями, характеристиками. Такое предварительное, приближенное представление объекта исследования называется концептуальной моделью. Этот этап является основой для последующего формального описания объекта.
2. Формализация операций. На основе содержательного описания определяется и анализируется исходное множество характеристик объекта, выделяются наиболее существенные из них. Затем выделяют управляемые и неуправляемые параметры, вводят символьные обозначения. Определяется система ограничений, строится целевая функция модели. Таким образом, происходит замена содержательного описания формальным (символьным, упорядоченным).
3. Проверка адекватности модели. Исходный вариант модели необходимо проверить по следующим аспектам:
1) все ли существенные параметры включены в модель?
2) нет ли в модели несущественных параметров?
3) правильно ли отражены связи между параметрами?
4) правильно ли определены ограничения на значения параметров?
Главным путем проверки адекватности модели исследуемому объекту выступает практика. После предварительной проверки приступают к реализации модели и проведению исследований. Полученные результаты моделирования подвергаются анализу на соответствие известным свойствам исследуемого объекта. По результатам проверки модели на адекватность принимается решение о возможности ее практического использования или о проведении корректировки.
4. Корректировка модели. На этом этапе уточняются имеющиеся сведения об объекте и все параметры построенной модели. Вносятся изменения в модель, и вновь выполняется оценка адекватности.
5. Оптимизация модели. Сущность оптимизации (улучшения) моделей состоит в их упрощении при заданном уровне адекватности. В основе оптимизации лежит возможность преобразования моделей из одной формы в другую. Основными показателями, по которым возможна оптимизация модели, являются время и затраты средств для проведения исследований и принятия решений с помощью модели.
|
|
|
32. Детерминированный и стохастический подходы к построению моделей.
Введение понятия «математическая схема» позволяет рассматривать математику не как метод расчёта, а как метод мышления, как средство формулирования понятий, что является наиболее важным при переходе от словесного описания системы к формальному представлению процесса её функционирования в виде некоторой математической модели (аналитической или имитационной). При пользовании математической схемой исследователя системы S в первую очередь должен интересовать вопрос об адекватности отображения в виде конкретных схем реальных процессов в исследуемой системе, а не возможность получения ответа (результата решения) на конкретный вопрос исследования.
Математическую схему можно определить как звено при переходе от содержательного к формальному описанию процесса функционирования системы с учётом воздействия внешней среды, т. е. имеет место цепочка «описательная модель – математическая схема – математическая (аналитическая или имитационная) модель».
Каждая конкретная система S характеризуется набором свойств, под которыми понимаются величины, отражающие поведение моделируемого объекта (реальной системы) и учитывающие условия её функционирования во взаимодействии с внешней средой (системой Е). При построении математической модели системы необходимо решить вопрос об её полноте. Полнота модели регулируется в основном выбором границы «система S – среда Е».
|
|
|
Модель объекта моделирования, т. е. системы S, можно представить в виде множества величин, описывающих процесс функционирования реальной системы и образующих в общем случае следующие подмножества:
а) совокупность входных воздействий на систему xi є X, i=1, nx;
б) совокупность воздействий внешней среды vl є V, l=1, nv;
в) совокупность внутренних параметров системы hk є H, k=1, nH;
г) совокупность выходных характеристик системы yi є Y, j=1, ny.
При этом в перечисленных подмножествах можно выделить управляемые и неуправляемые переменные. В общем случае xi, vl, hk, yi являются элементами непересекающихся подмножеств и содержат как детерминированные, так и стохастические составляющие.
При моделировании системы S входные воздействия, воздействия внешней среды Е и внутренние параметры системы являются независимыми (экзогенными) переменными, которые в векторной форме имеют соответственно вид 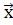 (t)=(x1(t), x2(t), …, xnX(t));
(t)=(x1(t), x2(t), …, xnX(t)); 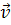 (t)=(
(t)=(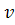 1(t),
1(t),  2(t),…,
2(t),…,  nV(t));
nV(t)); 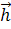 (t)=h1(t), h2(t), …, hnH(t)), а выходные характеристики системы являются зависимыми (эндогенными) переменными и в векторной форме имеют вид
(t)=h1(t), h2(t), …, hnH(t)), а выходные характеристики системы являются зависимыми (эндогенными) переменными и в векторной форме имеют вид 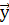 (t)=(y1(t), y2(t), …, ynY(t)).
(t)=(y1(t), y2(t), …, ynY(t)).
под математической моделью объекта (реальной системы) понимают конечное подмножество переменных { 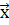 ,
, 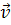 ,
, 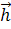 } вместе с математическими связями между ними и характеристиками
} вместе с математическими связями между ними и характеристиками 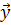 (t).
(t).
Если математическое описание объекта моделирования не содержит элементов случайности или они не учитываются, т.е. если можно считать, что в этом случае стохастическое воздействие внешней среды 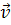 (t) и стохастические внутренние параметры
(t) и стохастические внутренние параметры 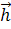 (t) отсутствуют, то модель называется детерминированной в том смысле, что характеристики однозначно определяются детерминированными входными воздействиями
(t) отсутствуют, то модель называется детерминированной в том смысле, что характеристики однозначно определяются детерминированными входными воздействиями
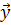 = f (
= f (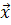 , t).
, t).
Очевидно, что детерминированная модель является частным случаем стохастической модели.
33. Особенности экономико-математического моделирования социально-экономических систем.
Социально-экономическая система – это сложная вероятностная динамическая система, охватывающая процессы производства, обмена, распределения и потребления материальных и других благ. Она относится к классу кибернетических систем, т.е. систем управляемых.
Исследуемое множество элементов можно рассматривать как систему, если выявлены следующие четыре признака:
1) целостность системы;
2) наличие цели и критерия исследования данного множества элементов;
3) наличие более крупной внешней по отношению к данной системы, называемой средой;
4) возможность выделения в данной системе взаимосвязанных частей (подсистем).
Основным методом исследования систем является метод моделирования, т.е. способ теоретического и практического действия, направленного на разработку и использование моделей. Метод моделирования основывается на принципе аналогии, т.е. возможности изучения реального объекта не непосредственно, а через рассмотрение подобного ему и более доступного объекта, его модели.
34. Классификация и примеры известных информационных систем в экономике.
Экономическая информационная система — это среда, составляющими элементами которой являются компьютеры, компьютерные сети, программные продукты, базы данных, персонал, технические и программные средства связи. Это система, направленная на достижение множества целей, одной из которых является производство информации, необходимой для поддержки принятия управленческих решений.
Информационные системы могут быть классифицированы по множеству признаков в зависимости от потребностей их изучения.
По характеру использования информации информационные системы можно разделить на информационно-поисковые и информационно-решающие системы.
Информационно-поисковые системы производят ввод, систематизацию, хранение, выдачу информации по запросу пользователя без сложных преобразований данных. Например, информационно-поисковая система в библиотеке, в железнодорожных и авиа кассах продажи билетов.
Информационно-решающие системы осуществляют все операции переработки информации по определенному алгоритму. Среди них можно провести классификацию по степени воздействия выработанной результатной информации на процесс принятия решений и выделить два класса: управляющие и советующие.
По характеру обрабатываемых данных выделяют информационно-справочные системы (ИСС) и системы обработки данных (СОД). ИСС выполняют поиск информации без ее обработки. АИСОД осуществляют как поиск, так и обработку информации.
Информационные системы, разрабатывающие альтернативы решений, могут быть модельными или экспертными.
Модельные информационные системы предоставляют пользователю математические, статистические, финансовые и другие модели, использование которых облегчает выработку и оценку альтернатив решения. Пользователь может получить недостающую ему для принятия решения информацию путем установления диалога с моделью в процессе ее исследования.
Экспертная система - это вычислительная система, построенная на основе формализованных эмпирических знаниях высококвалифицированных специалистов о некоторой конкретной проблемной области и которая в пределах этой области способна принимать экспертные решения. В рамках экспертных систем к настоящему моменту есть достижения в таких областях, как медицинская диагностика, геологическая разведка, экономический анализ.
По масштабу ЭИС можно классифицировать следующим образом:
- международные ЭИС; - государственные ЭИС; - региональные ЭИС; - отраслевые ЭИС; - ЭИС подотраслей; - ЭИС крупнейших транснациональных корпораций; - ЭИС объединений; - ЭИС корпораций; и т.д.
По числу пользователей ЭИС можно классифицировать следующим образом:
- однопользовательские (или персональные) - ЭИС, которые являются обособленными, не связанными и не взаимодействующими постоянно с другими ЭИС, а также используемые только своим непосредственным и единственным пользователем;
- многопользовательские (или распределенные) - ЭИС, в которых более чем один пользователь. В таких системах есть возможность позволить использование одного или нескольких компонентов одной или нескольких ЭИС и соответствующих им информационных технологий другими людьми (пользователями системы).
По сфере применения (предметной области) ЭИС можно классифицировать следующим образом:
- банковские ЭИС; - ЭИС фондового рынка; - страховые ЭИС; - налоговые ЭИС; - статистические ЭИС; - ЭИС промышленных предприятий; - ЭИС предприятий и организаций непромышленной сферы; - ЭИС предприятий и организаций сферы быта и сервиса;и т.д.
|
|
|
|
|
Дата добавления: 2015-04-23; Просмотров: 396; Нарушение авторских прав?; Мы поможем в написании вашей работы!