Можно найти, вычислив значение интеграла

60. -

Загальна будова

Хромомери

Супутники

Теломери

Нуклеосоми, хромонеми, хроматиди

ДНП

Хроматин

Гетерохроматичні ділянки

Гетерохроматин і тільця Барра

Еухроматичні ділянки

58. Рибосома (ribosome) є немембранною органелою клітини, що складається з рРНК та рибосомних білків

Рибосоми прокаріотів та еукаріотів є дуже подібними за будовою та функцією, але відрізняються розміром. Вони складаються з двох субодиниць: однієї великої та однієї малої. Для процесу трансляції необхідна злагоджена взаємодія обох субодиниць, що разом становлять комплекс із молекулярною масою декілька мільйонів дальтон (Da). Субодиниці рибосом за звичай позначаються одиницямиСведберга (S), що є мірою швидкості седиментації під час центрифугування і залежать від маси, розміру та форми частинки. Позначені в цих одиницях, велика субодиниця є 50S або 60S (прокаріотичні або еукаріотичні, відповідно), мала є 30S або 40S, і ціла рибосома (комплекс малої разом з великою) 70S або 80S.

Функція

Схематичне зображення рибосоми в процесітрансляції. Мала субодиниця зв'язує мРНК, а велика субодиниця напрямляє аміноацил-тРНК та пептидил-тРНК до матричної РНК, контролюючи правильне парування відповідних триплетів

Рибосома є органелою, на якій відбувається трансляція генетичної інформації закодованої в мРНК. Ця інформація втілюється в синтезований тут-же поліпептидний ланцюг. Рибосома несе двояку функцію: є структурною платформою для процесу декодування генетичної інформації з РНК, та володіє каталітичним центром відповідальним за формування пептидного зв’язку, так званим ‘пептидил-трансферазним центром’. Вважається що пептидил-трансферазна активність асоціюється з рРНК, і тому рибосома є рибозимом.

В клітині дозрілі рибосоми знаходяться переважно в компартментах, де активного білкового синтезу.

59 –

. (*Вставить υ⁴)

(!) 4. Если F(x) – плотность вероятности или функция распределения случайной величины х, то выражение

(*Ответ: )

или

Если F(x) – функция распределения случайной величины х, а f(x²) – некоторая функция этой величины, то

*C)

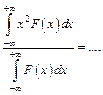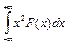(!) 5. Если F(x) – плотность вероятности или функция распределения случайной величины х, то выражение ; (*Ответы: и и )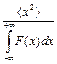

(!) 6. F(x) – плотность вероятности или функция распределения случайной величины х. Среднее значение на интервале от х₁ до х₂ равно:

*B) ;

(!) 7. Если F(x) – плотность вероятности или функция распределения случайной величины х, то равно:

*D)

(!) 8. Средние скорости молекул идеальных газов, у которых , а массы молекул > :

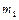*А) < ;

(!) 9. Если число молекул идеального газа выросло в четыре раза (N ₂=4 N ₁), а и , то относительное число молекул, имеющих скорости от 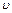до :

*С) осталось прежним;

(!) 10. f(p) - функция распределения по модулю импульса для молекул идеального газа. Среднее значение 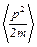равно:

*В) ;

11. Критерием перехода квантовой статистики в классическую принято значение μ равное …(*Ответ: 0 )

(!) 12. Молекулы идеального газа:

*С) могут иметь как целый, так и полу целый спин;

(!) 13. При одинаковых температурах наиболее вероятная скорость молекул кислорода … наиболее вероятной скорости молекул водорода. (*Вставить: меньше)

(!) 14. При одинаковых температурах средняя квадратичная скорость молекул кислорода … средней квадратичной скорости молекул водорода. (*Вставить: меньше)

(!) 15. При одинаковых температурах средняя энергия молекул кислорода … средней энергии молекул водорода. (*Вставить: равна)

(!) 16. Наиболее вероятное значение энергии для молекул идеального газа:

*D) не зависит от m.

(!) 17. Для функции распределения Максвелла по проекции импульса (*Ответ: 0,5 – запятая.)

(!) 18. Для функций распределения Максвелла по проекциям импульсов

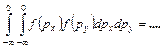(*Ответ: 0,25 – запятая.)

19. Среднее значение 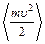для идеального газа можно рассчитать, пользуясь любым выражением, кроме …

*А) ;

20. Максимальное значение плотности вероятности с увеличением массы молекул (при Т =const) … (*Вставить: уменьшается)

(!) 21. В функции распределения Максвелла по проекции скорости 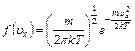m – это:

*А) масса одной молекулы определенного газа;

(!) 22. Плотность вероятности или функция распределения молекул идеального газа по проекции скорости имеет вид , где нормированный множитель 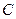равен:

*C) ;

(!) 23. Значения интеграла 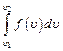для разных газов при одинаковых температурах:

*D) нельзя сравнить, так как значения интеграла зависят от выбранного

интервала скоростей.

(!) 24. Функция распределения молекул идеального газа по модулю скорости (плотность вероятности) имеет размерность:

*В) ;

(!) 25. Правильным соотношением для функции распределения молекул идеального газа по проекции импульса является:

*А)

(!) 26. На рисунке показано распределение Максвелла по модулю скорости для некоторого газа при разных температурах. При этом площади под кривыми (S_i) и температуры (Т_i) удовлетворяют соотношению:

*А) S₁=S₂=S₃=1, T₃>T₂>T₁;

(!) 27. Вероятность встретить молекулы идеального газа, у которых проекции скорости , , а принимает любые значения, равна…

(*Ответ: 0,25) – запятая.

(!) 28. - плотность вероятности или функция распределения молекул по энергии. Среднее значение молекулы идеального газа равно:

*В) ;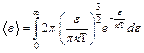

(!) 29. Среднее значение для молекул идеального газа равно любому выражению, кроме:

*D) + +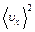

(!) 30. 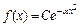- плотность вероятности или функция распределения случайной величины х, Нормированный множитель С равен:

*D) ;

(!) 31. Если и - плотности вероятности или функции распределения по проекциям скорости, то выражение

*В) 0

(!) 32. Отношение наиболее вероятных значений энергий для двух газов, у которых m₂=4m₁, a Т₂=Т₁, численно равно …(*Ответ: 1)

(!) 33. Распределение Максвелла-Больцмана для идеального газа имеет вид: 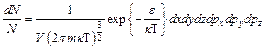, где -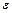

*В) потенциальная энергия частиц во внешнем поле плюс суммарная кинетическая энергия молекул

(!) 34. Для функций распределения 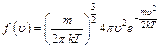и справедливо соотношение:

*В) ;

35. , , - плотности вероятности или функции распределения молекул по проекциям скорости, для которых справедливо любое соотношение, кроме …

*С) ;

(!) 36. 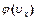- плотность вероятности или функция распределения по проекции скорости для молекул идеального газа принимает значения:

*С) ;

37. Если функция распределения по энергии для идеального газа пронормирована на число частиц (), то интеграл равен:

*D) суммарной энергии всех частиц, у которых

(!) 38. Наиболее вероятное значение проекции скорости для молекул идеального газа равно:

*C) 0;

(!) 39. Отношение средних значений для двух разных газов, у которых Т₁=3Т₂, а m₂=3m₁, равно …(*Ответ: 3)

(!) 40. - это *D) средняя квадратичная скорость, где m – масса одной молекулы.

(!) 41. Если отношение наиболее вероятных значений скоростей 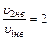, то отношение максимальных значений (*Ответ: 0.5) – запятая.

(!) 42. Распределение Максвелла по модулю скорости для некоторого идеального газа при Т₁>Т₂ показано на рисунке:

*В)

(!) 43. Функции распределения по проекции импульса р_х (плотность вероятности) для разных газов, у которых m₂>m₁, а 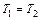, показаны на рисунке:

*В)

(!) 44. Функции распределения молекул идеального газа по проекции скорости (плотность вероятности) для разных газов, у которых m₂>m₁, a T₁=T₂, показаны на рисунке:

* В)

(!) 45. Функции распределения по энергии для некоторого газа при Т₂>Т₁ показаны на рисунке:

*С)

46. Правильным рисунком плотности вероятности f(v) для одинаковых газов, у которых , давление не меняется, а , является:

*С)

(!) 47. Если - плотность вероятности или функция распределения случайной величины х (х изменяется от -∞ до +∞), то справедливо любое выражение, кроме:

*D)

(!) 48. Если - плотность вероятности или функция распределения молекул идеального газа по энергии, то среднее значение на интервале энергий от до равно:

*D)

(!) 49. Если температура 2-х идеальных газов Т₂ =2 Т₁, а массы молекул m₂=2m₁, то отношение значений средних энергий (*Ответ: 2)

50. - функция распределения молекул идеального газа по энергии, которая удовлетворяет любому соотношению, кроме:

*D) .

(!) 51. Согласно теореме о равнораспределении энергии по степеням свободы равно:

*B)

(!) 52. При увеличении температуры идеального газа Т₂=4Т₁ отношение максимальных значений функций распределения по проекции скорости (*Ответ: 0,5 – запятая.)

(!) 53. - плотность вероятности или функция распределения молекул идеального газа по модулю скорости, для которой справедливо любое соотношение, кроме:

*А) ;

(!) 54. Средняя кинетическая энергия одного атома идеального газа равна 6,9·10^-21 Дж. Среднее значение (*Ответ: 2,3·10^-21Дж) Формат ответа: 2,3; -21

(!) 55. Если х - случайная физическая величина, принимающая ряд дискретных значений х₁, х₂, … х_п, а p_i – вероятность появления x_i, то среднее значение равно:

*А) ;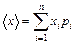

(!) 56. Выражение равно:

*D) 0.

(!) 57. Условием нормировки функции распределения Максвелла по модулю скорости для молекул идеального газа является выражение:

*С) ;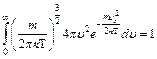

(!) 58. Интеграл 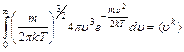, где k=…. (*Ответ: 1)

(!) 59. Графики 1,2,3 соответствуют трем функциям распределения Максвелла по модулю импульса для одного и того же газа в сосуде V при разных T. Наименьшей энтропии соответствует график ….. (*Ответ: 1)

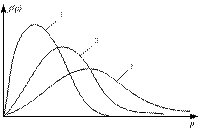
(!) 60. Среднее значение 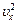можно найти, пользуясь любым выражением, кроме …

*С) ;

(!) 61. Если число молекул идеального газа увеличилось 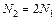, а , , 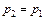, 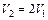то отношение вероятностей встретить молекулы с энергиями от 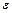до , 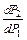=… (*Ответ: 1)

(!) 62. Функция распределения молекул идеального газа по проекции скорости , пронормированная на 1, имеет вид:

*В) ;

(!) 63. Для , плотности вероятности или функции распределения Максвелла по модулю скорости, справедливо выражение:

*А) ;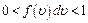

(!) 64. Функция распределения Максвелла по модулю скорости (плотность вероятности) f (υ) равна:

*С) относительному числу молекул в единичном интервале скоростей;

(!) 64,5. 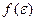- плотность вероятности или функция распределения молекул идеального газа по энергии. Заштрихованная площадь равна:

*D) относительному числу молекул 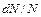, имеющих энергию от до

;

(!) 65. Основной постулат статической физики утверждает, что микросостояния, принадлежащие одной …, равновероятны. (Ответ: энергии)

(!) 66. , , - плотности вероятности или функции распределения молекул идеального газа по проекциям скорости. Выражение (*Ответ: 0,125 – запятая.)

67. Если 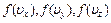- функции распределения по проекциям скоростей для молекул идеального газа, то:

*D)

68. Перейти от классической функции распределения по модулю импульса к функции распределения по модулю скорости f(u):

*B) можно, заменив p на mu и dp на mdu в выражении f(p)dp;

или

Перейти от классической функции распределения по модулю скорости к функции распределения по энергии f(e)

*C) можно, заменив на и du на в выражении f(u)du;

(!) 69. f(x²) – некоторая функция случайной величины x. Интеграл 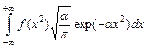равен: ;

70. Отношение интегралов для молекулы водорода Н₂ (молярная масса водорода 2×10^-3кг/моль) при Т=300 К с учетом N_A»6×10²³1/моль , где A и B – целые числа, значения которых перечислите через точку с запятой …, … без учета размерностей. (*Ответ: 5; -19)

(!) 71. Отношение максимальных значений функций распределения для молекул идеального газа . При этом отношение наиболее вероятных значений (*Ответ: 4)

(!) 72. Для молекул идеального газа значения интегралов и , где - наиболее вероятная энергия:

*B) I₁<I₂;

(!) 73. Для классической функции распределения по модулю скорости при условии

Т=const, а u₂>u₁ отношение ;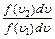

*D) >1, если u₁ и u₂ меньше u_нв;

*E) <1, если u₂ и u₁ больше u_нв;

(!) 74. Для данного газа в равновесном состоянии отношение средней энергии частиц к наиболее вероятной энергии при заданной температуре равно …

(*Ответ: 3)

(!) 75. Если f(u_x) – функция распределения молекул идеального газа по проекции скорости, то для интегралов: 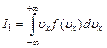, , 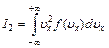справедливо следующее соотношение:

*D)

(!) 76. При T=const максимальное значение функции распределения по проекции импульса f(p_x):

*D)~ ;

(!) 77. Значения функций распределения по проекции скорости при , равной наиболее вероятной , для газов с молярными массами и соответственно равны: ; . С учетом T=const отношение (*Ответ: 9)

78. Значения функций распределения по проекции скорост и при , равной наиболее вероятной , для одного и того же газа при и соответственно равны ; . Отношение температур для этих функций распределения (*Ответ: 4)

(!) 79. Наиболее вероятное значение проекции скорости для молекул водорода Н₂ при Т=400 К равно … (*Ответ: 0)

80. Для молекулы азота N₂ (молярная масса азота 28 г/моль) наиболее вероятное значение модуля скорости при Т=300 К равна …. м/c. R=8,31 Дж/К×моль. Ответ округлите до десятков. (*Ответ: 420)

81. Для молекулы кислорода О₂ (молярная масса кислорода 32 г/моль) значение средней квадратичной скорости при Т=400 К равна ….. м/c. R=8,31 Дж/К×моль. Ответ округлите до десятков. (*Ответ: 560).

82. Случайная величина х принимает значения от 0 +¥. Функция распределения случайной величины х или плотность вероятности имеет вид , где нормировочный множитель С равен:

*A) b;

(!) 83. Основной постулат квантовой статистики - это...

*А) принцип тождественности частиц;

(!) 84. Основной постулат квантовой статистики (принцип тождественности) является следствием того, что...

*А) описание движения отдельной частицы носит вероятностный характер;

Дата добавления: 2015-04-24