Траектория - линия, описываемая мат. точкой в пространстве. Длина участка траектории пройдённого материальной точкой с момента начала отсчета наз. длиной пути

Оценка жизнеспособности проекта.

Для оценки жизнеспособности проекта сравнивают варианты проекта с точки зрения их стоимости, сроков реализации и прибыльности. В результате такой оценки инвестор (заказчик) должен быть уверен, что на продукцию, являющуюся результатом проекта, в течение всего жизненного цикла будет держаться стабильный спрос, достаточный для назначения такой цены, которая обеспечивала бы покрытие расходов на эксплуатацию и обслуживание объектов проекта, выплату задолженностей и удовлетворительную окупаемость капиталовложений.

Эта задача решается в рамках обоснования инвестиций (см. выше) и выполняется группой заказчика или независимой консультационной фирмой.

Оценка жизнеспособности проекта призвана ответить на следующие вопросы:

- возможность обеспечить требуемую динамику инвестиций;

- способность проекта генерировать потоки доходов, достаточных для компенсации его инвесторам вложенных ими ресурсов и взятого на себя риска.

В качестве базы сравнения как при наличии ряда альтернативных вариантов, так и единственного варианта принимается так называемая ситуация «без проекта». Это означает, что в случае проекта реконструкции предприятия следует сравнивать показатели проекта с показателями действующего предприятия, а при намерении строить новое предприятие — с ситуацией «без строительства нового предприятия».

Работа по оценке жизнеспособности проекта обычно проводится в 2

этапа:

Из альтернативных вариантов проекта выбирается наиболее жиз­неспособный;

Для выбранного варианта проекта подбираются методы финан­сирования и структура инвестиций, обеспечивающие максимальную жизнеспособность проекта.

Жизнеспособность проекта оценивают с помощью методов анализа эффективности.

DS= DS(t). Вектор Dr= r- r0, проведенный из начального положения движущейся точки в положение её в данный момент наз. перемещением.

Прямолинейное движение — механическое движение, при котором вектор перемещения ∆r не меняется по направлению и по величине равен длине пути, пройденного телом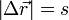

3. Криволинейное движение более сложный вид движения, чем прямолинейное, поскольку даже если движение происходит на плоскости, то изменяются две координаты, характеризующие положение тела. Скорость и ускорение тела также постоянно изменяются по направлению, а в общем случае и по модулю.

Мгновенная скорость тела при криволинейном движении направлена в любой точке траектории по касательной к траектории в этой точке.

Этот вывод о направлении мгновенной скорости можно подтвердить, наблюдая, как движутся брызги из-под колес буксующего автомобиля или искры при заточке деталей на вращающемся точильном камне.

При криволинейном движении направление скорости тела меняется, поэтому такое движение является неравномерным, даже если модуль скорости остается постоянным.

Ускорение при криволинейном движении: нормальное, тангенциальное, полное.

Тангенциальная составляющая ускорения - характеризует быстроту изменения скорости по модулю

Нормальная составляющая ускорения - направлена по нормали к центру кривизны - характеризует быстроту изменения скорости по направлению

Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих.

4. Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения. Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n. Вектор нормального ускорения направлен по радиусу кривизны траектории.

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

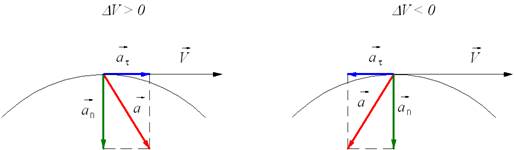
Направление вектора тангенциального ускорения τ (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.

5. Кругово́е движе́ние — это вращение по кругу, т.е. это круговой путь по круговой орбите. Оно может быть равномерным (с постоянной угловой скоростью) или неравномерным (с переменной угловой скоростью). Вращение трёхмерного тела вокруг неподвижной оси включает в себя круговое движение каждой его части. Мы можем говорить о круговом движении объекта только если можем пренебречь его размерами, так что мы имеем движение массивной точки на плоскости. Например, центр масс тела может совершать круговое движение.

Примеры кругового движения: искусственный спутник на геосинхронной орбите, камень на верёвке, вращающийся по кругу (см. метание молота), болид, совершающий поворот, электрон, движущийся перпендикулярно постоянному магнитному полю, зубчатое колесо, вращающееся внутри механизма.

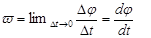6. Угловой скоростью наз. векторная величина, равная первой производной угла поворота тела по времени.

Угловым ускорением наз. векторная величина равная первой производной скорости по времени.При ускоренном движении вектор ε сонаправлен ω при замедленном противонаправлен.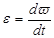

7.

8. Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние.

Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью. Поэтому первый закон Ньютона называют

также законом инерции.

Механическое движение относительно, и его характер зависит от системы отсчета. Первый закон Ньютона выполняется не во всякой системе отсчета, а те системы,

по отношению к которым он выполняется, называются инерциальными системами отсчета. Инерциальной системой отсчета является такая система, которая либо

покоится, либо движется равномерно и прямолинейно относительно какой-то другой инерциальной системы. Первый закон Ньютона утверждает существование инерциальных систем отсчета.

9. Масса тела — физическая величина, являющаяся одной из основных характеристик материи, определяющая ее инерционные (инертная масса) и гравитационные (гравитационная масса) свойства. В настоящее время можно считать доказанным, что инертная и гравитационная массы равны друг другу (с точностью, не меньшей 10^-12 их значения).

Сила – это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей, в результате которого тело приобретает ускорение или изменяет свою форму и размеры.

Соотношение (3) выражает второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).

В СИ коэффициент пропорциональности k = 1. Тогда

a = F /m, или F = m a = md v /dt(4)

Учитывая, что масса материальной точки (тела) в классической механике есть величина постоянная, в выражении (6.4) ее можно внести под знак производной:

F =(d/dt)(m v).(5)

Векторная величина

p = m v,(6)

численно равная произведению массы ма­териальной точки на ее скорость и име­ющая направление скорости, называется импульсом (количеством движения) этой материальной точки.

Подставляя (6) в (5), получим

F =d p /dt(7)

Это выражение — более общая формули­ровка второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе.

10. 3 закон Ньютона: 2 тела действуют друг на друга с силами, направленными вдоль одной прямой. Эти силы равны по величине и противоположны по направлению. 3-ий закон позволяет перейти от динамики отдельной матерьяльной точки к динамике системы матерьяльных точек. Это следует из того, что и для сист.мат. точек взаимодействия этих матерьяльных точек сводятся к парным взаимодействиям.

Пример: 1).В известной игре «перетягивание каната» обе партии действуют друг на друга (через канат) с одинаковой силой, как это следует из закона действия и противодействия. Значит, выиграет (перетянет канат) не та партия, которая сильнее тянет — тянут обе партии с одинаковой силой,— а та, которая сильнее упирается в Землю.

2). Возьмем в руки два одинаковых динамометра, сцепим их крюками и будем тянуть в разные стороны (рис. 18). Оба динамометра покажут одинаковые по модулю силы натяжения, т. е. F1=-F2.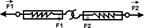

11. И́мпульс (Количество движения) — векторная физическая величина, характеризующая меру механического движения тела. В классической механике импульс тела равен произведению массы m этой точки на её скорость v, направление импульса совпадает с направлением вектора скорости: .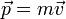

Дата добавления: 2015-04-24