Уравнений методом Гаусса

Метод Гаусса (или метод последовательного исключения неизвестных) применим для решения систем линейных уравнений, в которых число неизвестных может быть либо равно числу уравнений, либо отлично от него.

Система т линейных уравнений с п неизвестными имеет вид:

x ₁, x ₂, …, x_n – неизвестные.

a_{i j} - коэффициенты при неизвестных.

b_i - свободные члены (или правые части)

Система линейных уравнений называется совместной, если она имеет решение, и несовместной, если она не имеет решения.

Совместная система называется определенной, если она имеет единственное решение и неопределенной, если она имеет бесчисленное множество решений.

Две совместные системы называются равносильными, если они имеют одно и то же множество решений.

К элементарным преобразованиям системы отнесем следующее:

1. перемена местами двух любых уравнений;

2. умножение обеих частей любого из уравнений на произвольное число, отличное от нуля;

3. прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число.

Элементарные преобразования переводят систему уравнений в равносильную ей.

Элементарные преобразования системы используются в методе Гаусса.

Для простоты рассмотрим метод Гаусса для системы трех линейных уравнений с тремя неизвестными в случае, когда существует единственное решение:

Дана система:

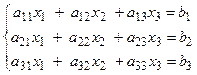(1)

1-ый шаг метода Гаусса.

На первом шаге исключим неизвестное х₁ из всех уравнений системы (1), кроме первого. Пусть коэффициент . Назовем его ведущим элементом. Разделим первое уравнение системы (1) на а₁₁. Получим уравнение:

(2)

где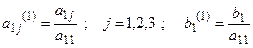

Исключим х₁ из второго и третьего уравнений системы (1). Для этого вычтем из них уравнение (2), умноженное на коэффициент при х₁ (соответственно а ₂₁ и а ₃₁).

Система примет вид:

(3)

Верхний индекс (1) указывает, что речь идет о коэффициентах первой преобразованной системы.

2-ой шаг метода Гаусса.

На втором шаге исключим неизвестное х₂ из третьего уравнения системы (3). Пусть коэффициент 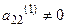. Выберем его за ведущий элемент и разделим на него второе уравнение системы (3), получим уравнение:

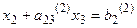(4)

где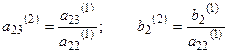

Из третьего уравнения системы (3) вычтем уравнение (4), умноженное на Получим уравнение:

Предполагая, что 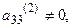находим

В результате преобразований система приняла вид:

(5)

Система вида (5) называется треугольной.

Процесс приведения системы (1) к треугольному виду (5) (шаги 1 и 2) называют прямым ходом метода Гаусса.

Нахождение неизвестных из треугольной системы называют обратным ходом метода Гаусса.

Для этого найденное значение х₃ подставляют во второе уравнение системы (5) и находят х₂. Затем х₂ и х₃ подставляют в первое уравнение и находят х₁.

В общем случае для системы т линейных уравнений с п неизвестными проводятся аналогичные преобразования. На каждом шаге исключается одно из неизвестных из всех уравнений, расположенных ниже ведущего уравнения.

Отсюда другое называние метода Гаусса – метод последовательного исключения неизвестных.

Если в ходе преобразований системы получается противоречивое уравнение вида 0 = b, где b ¹ 0, то это означает, что система несовместна и решений не имеет.

В случае совместной системы после преобразований по методу Гаусса, составляющих прямой ход метода, система т линейных уравнений с п неизвестными будет приведена или к треугольному или к ступенчатому виду.

Треугольная система имеет вид:

Такая система имеет единственное решение, которое находится в результате проведения обратного хода метода гаусса.

Ступенчатая система имеет вид:

№10.СЛУ.Метод обратной матрицы

Сейчас разберем алгоритм решения системы уравнений, используя метод обратной матрицы:

1. Данную систему уравнений необходимо записать в матричной форме:

2. Выразить неизвестные переменные:

Мы видим, что решение матричным способом сводится к умножению обратной матрицы к матрице А на матрицу свободных членов. т.е. матрицу В. Вот на этом то этапе нам и нужны навыки нахождения обратной матрицы.

3. Итак, найдем матрицу обратную матрице А:

Сначала рассчитаем определитель основной матрицы:

Определитель не равен нулю, значит обратная матрица существует. Найдем 9 дополнений матрицы:

Для первой строки:

Для второй строки:

Для третьей строки:

4. Составим обратную матрицу:

5. Вернемся к матричной форме записи системы уравнений и выраженным неизвестным, подставим в эту форму полученные данные:

6. Остается перемножить две матрицы:

Итак, метод обратной матрицы привел нас к ответу: x=1, y=2, z=3.

Дата добавления: 2015-04-24