Сортировка массивов. Методы сортировки (общие сведения)

Пример

В приведённом ниже примере осуществляется ввод и вывод двумерного массива А размерностью 10*15. Формирование и вывод массива описаны в виде двух процедур, которые вызываются последовательно из основной программы. Надо заметить, что формирование двумерного массива можно осуществлять всеми тремя способами, описанными для одномерных массивов, то есть: ввод с клавиатуры, через генератор случайных чисел или с помощью файла. Пусть в нашем примере элементы задаются генератором случайных чисел.

Program Example_45;
Const n = 2; m = 15;
Type dmyarray = Array[1..n., 1..m] Of Integer;
Var A: dmyarray;

Procedure Init(Var x: dmyarray); {процедура формирования массива}
Var i, j: Integer;
Begin
For i:=1 To n Do
For j:=1 To m Do
x[i,j]:=-25+Random(51);
End;

Procedure Print(x: dmyarray); {процедура вывода массива на экран}
Var i, j: Integer;
Begin
For i:=1 To n Do
Begin {ввод i-ой строки массива}
For j:=1 To n Do Write(x[i,j]:5);
Writeln; {переход на начало следующей строки}
End;

Begin {основная программа}
Init(A); {вызов процедуры формирования массива}
Writeln('Массив А:');
Print(A); {вызов процедуры вывода}
Readln;
End.

При решении задачи сортировки обычно выдвигается требование минимального использования дополнительной памяти, из которого вытекает недопустимость применения дополнительных массивов.
Для оценки быстродействия алгоритмов различных методов сортировки, как правило, используют два показателя:
- количество присваиваний;
- количество сравнений.
Все методы сортировки можно разделить на две большие группы:
- прямые методы сортировки;
- улучшенные методы сортировки.
Прямые методы сортировки по принципу, лежащему в основе метода, в свою очередь разделяются на три подгруппы:
1. сортировка вставкой (включением);
2. сортировка выбором (выделением);

Сортировка вставкой.
Массив разделяется на две части: отсортированную и неотсортированную. Элементы из неотсортированной части поочередно выбираются и вставляются в отсортированную часть так, чтобы не нарушить в ней упорядоченность элементов. В начале работы алгоритма в качестве отсортированной части массива принимают только один первый элемент, а в качестве неотсортированной части – все остальные.
Сортировка выбором.
Находим (выбираем) в массиве элемент с минимальным значением на интервале от 1-го до n-го (последнего) элемента и меняем его местами с первым элементом. На втором шаге находим элемент с минимальным значением на интервале от 2-го до n-го элемента и меняем его местами со вторым элементом.
И так далее для всех элементов до n-1-го.
Сортировка обменом («пузырьковая сортировка»).
Слева направо поочередно сравниваются два соседних элемента, и если их взаиморасположение не соответствует заданному условию упорядоченности, то они меняются местами. Далее берутся два следующих и так далее до конца массива.
После одного такого прохода на последней n-ой позиции массива будет стоять максимальный элемент, поэтому второй проход обменов выполняется до n-1-го элемента. И так далее.

Теоретические и практические исследования алгоритмов прямых методов сортировки показали, что как по числу сравнений, так и по числу присваиваний они имеют квадратичную зависимость от длины массива п. Исключение составляет метод выбора, который имеет число присваиваний порядка n*ln(n). Это свойство алгоритма выбора полезно использовать в задачах сортировки в сложных структурах данных, когда на одно сравнение выполняется большое число присваиваний. В таких задачах метод выбора успешно конкурирует с самыми быстрыми улучшенными методами сортировки.
Если сравнить рассмотренные прямые методы между собой, то в среднем методы вставки и выбора оказываются приблизительно эквивалентными и в несколько раз (в зависимости от длины массива) лучше, чем метод обмена ("пузырька").

Улучшенные методы сортировки
Ни один из представленных выше методов сортировки не является оптимальным. Обычно алгоритм оптимизируют под конкретную задачу, например, мы знаем, что на входе имеется массив, в котором первые k элементов упорядочены. Тогда лишено смысла тупо использовать алгоритм сортировки, так как имеется возможность его улучшить, убрав несколько действий. Для нашего примера используем метод сортировки выбором. Для наглядности поставим конкретные условия задачи.
Задан массив чисел. Первые элементы упорядочены, последние – нет. Упорядочить весь массив.

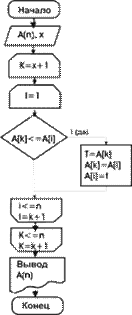
То есть мы упростили алгоритм, уменьшив колличество циклов и действий в нем.
Однако есть и такая оптимизация, которая подойдет почти для всех программ.

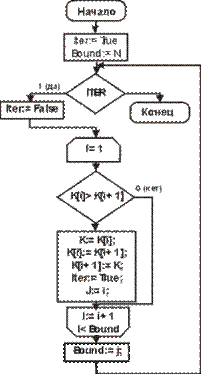
Например, оптимизируем метод сортировки "пузырьком". Теоритически усовершенствовать алгоритм можно, введя дополнитнльно переменную булевского типа (переменная Iter на рисунке снизу), которая будет показывать, были ли произведены изменения после n-ного прохода. Если нет, то массив уже отсортирован. Если да, то запоминается место последней перестановки (переменная J на рисунке снизу), определяющее границы счетчика (переменная I) при следующем прогоне. Следует заметить, что повторный вход в цикл со счетчиком произойдет только если за предыдущий проход цикла были произведены какие-либо изменения. Таким образом, исключаются дальнейшие бесполезные проходы.

20. Сортировка массивов. Метод прямого выбора: общая схема алгоритм программа.

Схема

Блок-схема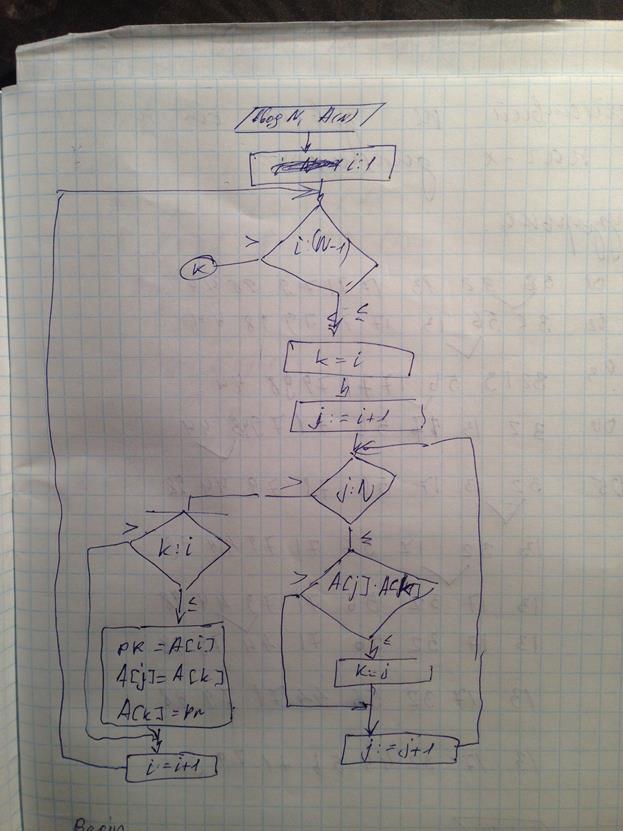

Текст программы

21. Метод прямого обмена: общая схема, алгоритм, программа.

Схема и блок-схема

Дата добавления: 2015-04-24