Экспоненциальный рост численности популяции, уравнение, лабораторные и натурные примеры

Прирост популяции пропорционален ее численности, и поэтому, если рост популяции не ограничивают никакие внешние факторы, популяция растет ускоренно. Опишем этот рост математически. Рост численности с постоянной скоростью называется экспоненциальным ростом.

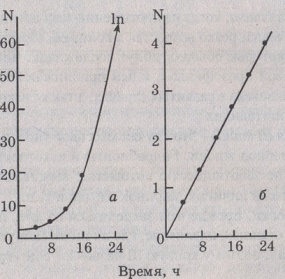
Эта закономерность роста выражается кривой одноклеточного организма, делящегося каждые 4 часа: а — арифметическая шкала; б — логарифмическая шкала

На современном математическом языке эта кривая отражает экспоненциальный рост численности организмов и описывается уравнением: N=Ne", tо', где: Nt—численность популяции в момент времени t; No—численность популяции в начальный момент времени t0; е — основание натурального логарифма (2,7182); г — показатель, характеризующий темп размножения особей в данной популяции – репродуктивный потенциал.

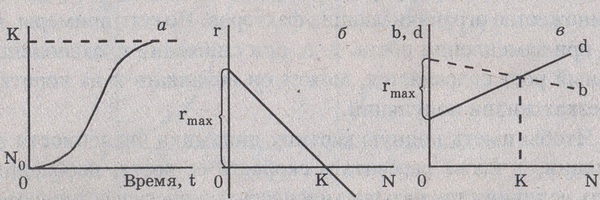, при начальной численности N скорость роста имеет максимальное значение rmax, а при HF = К га = 0. В результате решения уравнения логистической кривой получаем зависимость: Nt= K/(1+ea"rmaxt), нре Nt — численность популяции в момент времени t; е — основание натурального логарифма; а — постоянная итерирования. Величину К называют еще емкостью среды в отношении особей данной популяции. Здесь речь идет о биологической емкости среды — степени способности природного или при-родно-антропогенного окружения обеспечивать нормальную жизнедеятельность (дыхание, питание, размножение, отдых и т.п.) определенному числу организмов и их сообществ без заметного нарушения самого окружения (Реймерс, 1990).

Пока N невелико, на прирост популяции основное влияние оказывает сомножитель rN и рост популяции ускоряется. Когда становится достаточно высоким, на численность популяции начинает оказывать основное влияние сомножитель (K-N)/K и рост популяции начинает замедляться. Когда N=K, (K-N)/K=0 и рост численности популяции прекращается.

При всей своей простоте логистическое уравнение удовлетворительно описывает много наблюдаемых в природе случаев и до сих пор с успехом используется в математической экологии.

Дата добавления: 2015-04-24