Измерение длин линий оптическими дальномерами. Принцип измерения расстояния нитяным дальномером

Решение обратной геодезической задачи.

Билет 16.

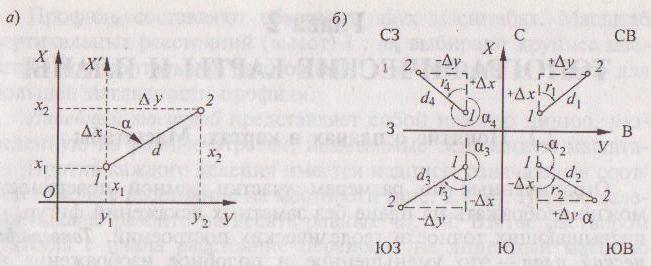
По известным координатам x1, y1 и x2, y2 отрезка прямой 1-2 вычисляют его длину d, румб r1-2 и дирекционный угол а. Вначал находят румб направления 1-2 по значению его тангенса:

tg r1-2 = Δy/ Δx=(y2-y1)/(x2-x1).

Затем по знакам разностей y2-y1 и x2-x1 определяют четверть и наименование румба, а также дирекционный угол а1-2. Длину отрезка 1-2 вычисляют для контроля по двум из трех следующих формул:

d=(x2-x1)/cos(a); d=(y2-y1)/sin(a); d=sqrt((Δx)^2+ (Δy)^2).

Оптический дальномер.

В дальномерах измеряется не сама длина линии, а некоторая другая величина,

относительно которой длина линии является функцией. В геодезии применяют 3 вида дальномеров:

оптические(дальномеры-геометрического-типа),

электрооптические (светодальномеры),

радиотехнические (радиодальномеры).

Геометрическая схема оптических дальномеров. Пусть требуется найти расстояние АВ. Поместим в точку А оптический дальномер, а в точку В перпендикулярно линии АВ – рейку.

Обозначим:_l–отрезок_рейки_GM,

φ – угол, под которым этот отрезок виден из точки А.

Из треугольника АGВ имеем:

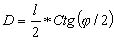(4.31)

или

D = l * Ctg(φ). (4.32)

Обычно угол φ небольшой (до 1), и, применяя разложение функции Ctgφ в ряд, можно привести формулу (4.31) к виду (4.32). В правой части этих формул два аргумента, относительно которых расстояние D является функцией. Если один из аргументов имеет постоянное значение, то для нахождения расстояния D достаточно измерить только одну величину. В зависимости от того, какая величина – φ или l, – принята постоянной, различают дальномеры с постоянным углом и дальномеры с постоянным базисом.

В дальномере с постоянным углом измеряют отрезок l, а угол φ – постоянный; он называется диастимометрическим углом.

В дальномерах с постоянным базисом измеряют угол φ, который называется параллактическим углом; отрезок l имеет постоянную известную длину и называется базисом.

Дата добавления: 2015-04-24