Вычисление средних показателей динамики

Средний уровень ряда 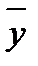называется средней хронологической.

Средняя хронологическая − это средняя величина из показателей, изменяющихся во времени.

В интервальном ряду с равными интервалами средний уровень ряда определяется по формуле простой средней арифметической.

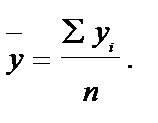
Средний уровень ряда в интервальном ряду динамики требует, чтобы было указано, за какой период времени он вычислен (среднемесячный, среднегодовой и т.д.).

Пример 1 Имеются следующие данные о товарообороте, ден.ед.:

Месяц	январь	февраль	март
Товарооборот

Вычислить среднемесячный товарооборот за первый квартал.

Т.к. нам дан интервальный ряд с равными интервалами, применим формулу простой средней арифметической:

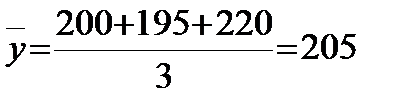
Если интервальный ряд имеет разные интервалы, то его вначале нужно привести к ряду с равными интервалами, а затем можно будет использовать формулу простой средней арифметической.

Пример 2 Имеются следующие данные о товарообороте, ден.ед.:

Месяц	январь	февраль	март	2-ой квартал
Товарооборот

Будем считать, что во втором квартале товарооборот распределялся по месяцам равномерно, тогда среднемесячный товарооборот за 1-ое полугодие:

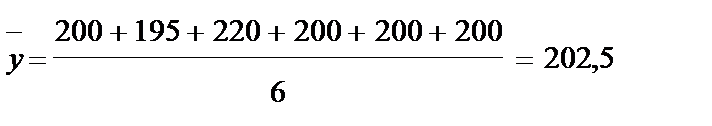
Так как показатели моментных рядов не обладают свойством суммарности, то среднюю нельзя вычислить, применяя формулу простой средней арифметической, в связи с тем, что остатки менялись непрерывно в течение месяца, а данные приводятся на определённый день.

Поэтому мы воспользуемся приближенным методом, основанным на предположении, что изучаемое явление менялось равномерно в течение каждого месяца. Чем короче будет интервал ряда, тем меньше ошибка будет допущена при использовании этого допущения.

Получим формулу:

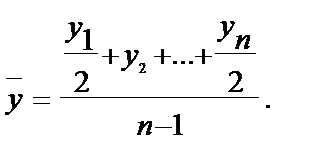
Эта формула применяется для вычисления среднего уровня в моментных рядах с равными интервалами.

Пример 3 Имеются данные об остатках строительных материалов на начало месяца, ден. ед.:

На дату	1.01	1.02	1.03	1.04
Остатки

Определить средний остаток за 1-й квартал.

Решение.

.

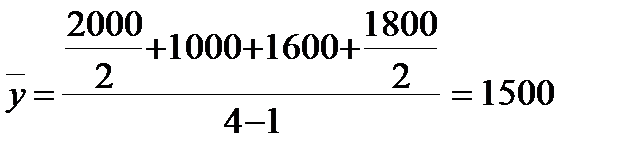Если интервалы в моментных рядах не равны, то средний уровень ряда вычисляется по формуле:

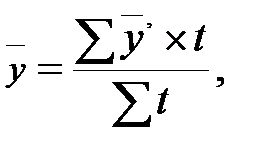
где 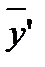- средний уровень в интервалах между датами,

t - период времени (интервал ряда)

Пример 4 Имеются данные об остатках сырья и материалов, ден. ед

На дату	01.01	01.02	01.03	01.04	01.07
Остатки

Найти среднемесячные остатки сырья и материалов за первое полугодие.

Применяем формулу:

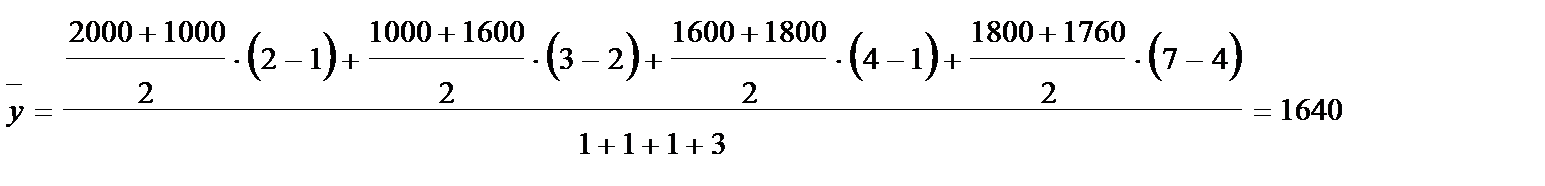
Средний абсолютный прирост вычисляется двумя способами:

1 Как средняя арифметическая простая годовых (цепных) приростов, т.е.

.

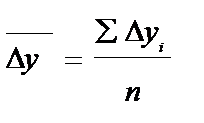2 Как частное от деления базисного прироста к числу периодов:

.

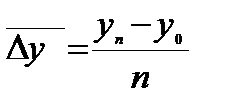Расчет среднего абсолютного значения 1% прироста за несколько лет производится по формуле простой средней арифметической:

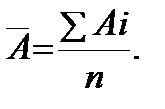
При вычислении среднегодового темпа роста нельзя применять простую среднюю арифметическую, т.к. сумма годовых темпов не будет иметь смысла. В этом случае применяют среднюю геометрическую, т.е.:

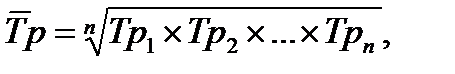
где Тр_i − годовые цепные темпы роста;

n − число темпов.

Поскольку произведение цепных темпов равно темпу базисному, то средний темп роста может быть рассчитан следующим образом:

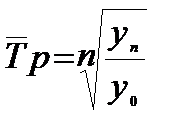
При расчёте по этой формуле не обязательно знать годовые темпы роста. Величина среднего темпа будет зависеть от соотношения начального и конечного уровня ряда.

Пример 5 Номинальная заработная плата работников народного хозяйства Республики Беларусь характеризуется данными, представленными в таблице 1.

Таблица 1 – Номинальная заработная плата работников народного хозяйства Республике Беларусь

Год
Размер заработной платы, тыс.р.	558,9	1123,0	1189,2	2250,7	3347,5	4463,7	5582,2	7701,1

Для анализа динамики заработной платы определить:

1 среднегодовой размер заработной платы за 8 лет;

2 ежегодные и базисные абсолютные приросты, темпы роста и прироста заработной платы;

3 абсолютное значение 1% прироста;

4 среднегодовой абсолютный прирост;

5 среднегодовой темп роста и среднегодовой темп прироста;

6 среднее значение 1% прироста.

Результаты представить в таблице, сделать выводы.

Дата добавления: 2015-04-24