Алгоритм. 1. Шаг 1. Задаются начальные границы отрезка и число итераций , рассчитывают начальные точки деления:

Шаг 3.

Алгоритм

1. Шаг 1. Задаются начальные границы отрезка 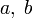и число итераций , рассчитывают начальные точки деления: и значения в них целевой функции: .

2. Шаг 2. .

· Если , то .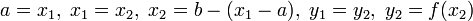

· Иначе .

· Если 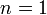, то 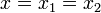и останов.

· Иначе возврат к шагу 2.

5. В чем состоят достоинства и недостатки метода Фибоначи?

Недостаток метода Фибоначчи состоит в том, что стратегия поиска существенно зависит от заранее заданного числа шагов поиска.

6. Что такое «золотое сечение»? В чем заключается сущность метода золотого сечения?

Золотое сечение (золотая пропорция, деление в крайнем и среднем отношении) — делениенепрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.

Отношение большей части к меньшей в этой пропорции выражается квадратичной иррациональностью

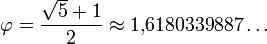
и, наоборот, отношение меньшей части к большей

Число называется также золотым числом.

В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (ок. 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.

Лука Пачоли, современник и друг Леонардо да Винчи, называл это отношение «божественной пропорцией». Термин «золотое сечение» (goldener Schnitt) был введён в обиход Мартином Омом в 1835 году.

Золотое сечение имеет множество замечательных свойств, но ещё больше свойств вымышленных

Метод золотого сечения — метод поиска значений действительно-значной функции на заданном отрезке. В основе метода лежит принцип деления в пропорцияхзолотого сечения. Наиболее широко известен как метод поиска экстремума в решении задач оптимизации

Описание метода

Пусть задана функция 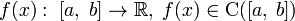. Тогда для того, чтобы найти определённое значение этой функции на заданном отрезке, отвечающее критерию поиска (пусть это будет минимум), рассматриваемый отрезок делится в пропорции золотого сечения в обоих направлениях, то есть выбираются две точк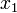и и такие, что:

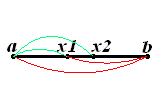
Иллюстрация выбора промежуточных точек метода золотого сечения.

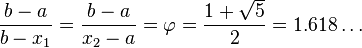, где 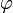— пропорция золотого сечения.

Таким образом:

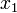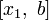То есть точка делит отрезок в отношении золотого сечения. Аналогично делит отрезок в той же пропорции. Это свойство и используется для построения итеративного процесса.

· 1) На первой итерации заданный отрезок делится двумя симметричными относительно его центра точками и рассчитываются значения в этих точках.

· 2) После чего тот из концов отрезка, к которому среди двух вновь поставленных точек ближе оказалась та, значение в которой максимально (для случая поискаминимума), отбрасывают.

· 3) На следующей итерации в силу показанного выше свойства золотого сечения уже надо искать всего одну новую точку.

· 4) Процедура продолжается до тех пор, пока не будет достигнута заданная точность.

Дата добавления: 2015-04-24