В чем Аристотель видел трудности познания

Шаг 3.

Формализация

1. Шаг 1. Задаются начальные границы отрезка 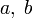и точность .

2. Шаг 2. Рассчитывают начальные точки деления: 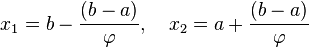и значения в них целевой функции: .

· Если 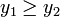(для поиска max изменить неравенство на 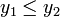), то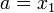

· Иначе .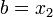

· Если 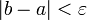, то 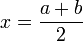и останов.

· Иначе возврат к шагу 2.

7.Как связаны между собой метод Фибоначчи и метод золотого сечения?

Метод почти половинного деления требует на каждой итерации двух вычислений значений функции: в точках 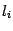и 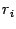. Имеются два схожих по идее, но более экономных метода, в которых каждая итерация требует только одного нового вычисления значения функции. Если основные вычислительные усилия на каждой итерации приходятся именно на вычисление значений функции (так, как правило, и бывает), то это приводит к ускорению вычислений примерно вдвое по сравнению с методом почти половинного деления.

Один из методов называется метод золотого сечения. В этом методе длины последовательных отрезков должны давать одно и то же число :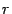

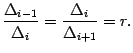
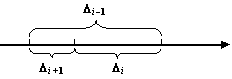
Рис.9.17.Три последовательных отрезка

При этом 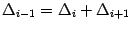, откуда легко получить, что число 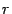удовлетворяет равенству 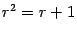. Решая это уравнение, получаем, что 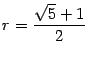. Таким образом, на первом шаге на отрезке 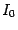вычисляются значения в двух точках 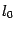и 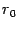, расположенных симметрично на расстоянии 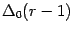от концов отрезка 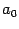и 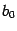и делящих отрезок на части, составляющие "золотое сечение". Сравнивая точно так же, как в методе почти половинного деления, значения в этих точках, выбираем в качестве 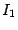либо 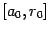, либо 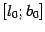. Экономия по сравнению с методом почти половинного деления получается на всех остальных шагах, поскольку если процесс повторить на отрезке при , то одной из точек деления оказывается ранее найденная точка: либо 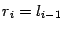, так что одно из двух значений функции найдено на предыдущей итерации.

Ещё один метод -- метод Фибоначчи -- применяется в тех случаях, когда заранее известно, сколько итераций мы собираемся совершить, и при этом хотим получить наибольшую возможную точность в определении точки минимума. При этом оказывается, что длины отрезков связаны с последовательностью чисел Фибоначчи 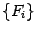, заданной начальными значениями 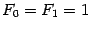и рекуррентной формулой .

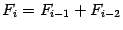8. В чем заключается достоинство метода золотого сечения?

Метод отличается высокой скоростью сходимости, обычно изысканной компактностью программной реализации и всегда находит точку, минимальную на заданном интервале.

9. В чем заключается сущность аналитических методов оптимизации?

Группа аналитических методов оптимизации объединяет аналитический поиск экстремума функции, метод множителей Лагранжа,вариационные методы и принцип максимума. Аналитический поиск экстремума функции, заданных без ограничений на независимые переменные является наиболее простым, но применяется к задачам, у которых оптимизируемая функция имеет аналитическое выражение, дифференцируемое во всем диапазоне исследования, а число переменных невелико.

Аналитический метод оптимизации предусматривает аналитическое задание соответствующих функций и определение производных от них. В случае наличия таких ограничений, касающихся переменных величин, полезным может оказаться хорошо известный в математике метод множителей Лагранжа.

Группааналитических методов оптимизации объединяет аналитический поиск экстремума функций, заданных без ограничений, метод множителей Лагранжа, вариационные методы и принцип максимума.

Для использованияаналитических методов оптимизации необходимо, чтобы расчетная формула критерия, ограничения и связи между координатами, управлениями и независимой переменной, а также начальные и конечные условия были представлены в форме функций, которые могут быть по крайней мере один раз дифференцируемыми и могут иметь конечное число точек разрывов.

Не отрицая значенияаналитических методов оптимизации процесса бурения, авторы настоящей работы отдали предпочтение графо-аналитическим методам, тем более, что последние применительно к некоторым методам проводки стволов скважин больших диаметров не освещены в литературе.

На основании изложенного можно заключить что разработка и усовершенствованиеаналитических методов оптимизации газовых сетей сохраняют свое значение.

На основании изложенного можно заключить, что разработка и усовершенствованиеаналитических методов оптимизации газовых сетей сохраняют свое значение.

В книге пятой настоящей серии Справочников (в главе 6 первого раздела) излагаются основные математические методы решения экстремальных задач, лежащие в основеаналитических методов оптимизации. Поэтому в настоящей главе основное внимание уделено экспериментально-статистическим методам: оптимизации, а также вопросам применения методов к задачам управления в химической технологии. В связи с этим глава делится на две части.

Аналитические или классические ме­тоды оптимизации связаны с использованием возможностей и применением средств дифференциального и вариационного исчислений для определения экстремума функции це­ди. Эти методы позволяют определить точки, удовлетворяющие лишь необходимым признакам локальных экстремумов, для чего используются частные производные функции цели по параметрам. Поэтому применение классических методов возможно, только:

1.
Если известно аналитическое выражение функции цели от параметров;

2.
если эта функция дважды дифференцируема по параметрам.

Аналитической моделью называется такое формализованное описание системы, которое позволяет получить решение уравнения в явном виде, используя известный математический аппарат.

10. В чем состоят достоинства и недостатки аналитических методов оптимизации?

Достоинство аналитических методов заключается в возможности

получения решения в явной аналитической форме, позволяющей проводить детальный анализ процессов, протекающих в исследуемой системе, в широком диапазоне изменения параметров системы. Результаты в аналитической форме являются основой для выбора оптимальных вариантов структурно-функциональной организации системы на этапе синтеза.

Недостаток аналитических методов – использование целого ряда допущений и предположений в процессе построения математических моделей и невозможность, в некоторых случаях, получить решение в явном виде из-за неразрешимости уравнений в аналитической форме, отсутствия первообразных для подынтегральных функций и т.п. В этих случаях широко применяются численные методы.

11. В чем состоит сущность метода равномерного поиска(перебора)?

В сущности, перебор - это решение задач, возникающих из заданной, когда значение некоторого искомого параметра фиксируется различным образом, и производится выбор того из рассмотренных значений, которое дает наиболее подходящее решение. Часто каждая из рассматриваемых задач с фиксированным значением данного параметра в свою очередь решается переборными методами. Тогда говорят о многоуровневом или иерархически устроенном алгоритме. Основываясь на столь общем определении перебора, можно дать лишь тривиальные рекомендации о способах его выполнения (однако, и они иногда полезны). К счастью, рассматриваемые задачи, кроме возможности их решения методами перебора, обычно имеют и другие характерные общие особенности. Это позволяет создавать, изучать и применять общие методы перебора.

Основная задача при реализации переборных методов заключается в нахождении такого порядка элементов перебора, при котором искомый элемент встретится как можно раньше. Это задача сокращения перебора. Существуют и другие проблемы, связанные с этим методом, например, проблема оптимизации генерации элементов перебора, но о них здесь речи не пойдет.

12. В чем состоит сущность метода Гаусса – Зейделя?

Метод Зейделя (иногда называемый методом Гаусса-Зейделя) является модификацией метода простой итерации, заключающейся в том, что при вычислении очередного приближения x^(k+1) его уже полученные компоненты x₁^(k+1),...,x_{i - 1}^(k+1) сразу же используются для вычисления x_i^(k+1).

В координатной форме записи метод Зейделя имеет вид:

x₁^(k+1) = c₁₁x₁^(k) + c₁₂x₂^(k) +... + c_1n-1x_n-1^(k) + c_1nx_n^(k) + d₁
x₂^(k+1) = c₂₁x₁^(k+1) + c₂₂x₂^(k) +... + c_2n-1x_n-1^(k) + c_2nx_n^(k) + d₂
...
x_n^(k+1) = c_n1x₁^(k+1) + c_n2x₂^(k+1) +... + c_nn-1x_n-1^(k+1) + c_nnx_n^(k) + d_n
где x⁽⁰⁾ - некоторое начальное приближение к решению.

Таким образом i -тая компонента (k+1)-го приближения вычисляется по формуле

xi^(k+1) = ∑ j=1^i-1 cijxj^(k+1) + ∑ ^nj=i cijxj^(k) + di, i = 1,..., n

(1.20)

Условие окончания итерационного процесса Зейделя при достижении точности ε в упрощенной форме имеет вид:

|| x ^(k+1) - x ^(k) || ≤ ε.

Существует более точное условие окончания итерационного процесса, которое более сложно и требует дополнительных вычислений

13. В чем состоят достоинства и недостатки метода Гаусса – Зейделя?

По простоте и удобству реализации предложенный метод обладает всеми достоинствамиметода Гаусса-Зейделя. [ 9 ]

Гаусса, квадратных корней и др.) и интегральные (например, метод Гаусса-Зейделя) методы. Аппроксимация уравнения (10.50) осуществляется путем представления интеграла в виде конечной суммы, что легко осуществляется обычно в связи с тем, что практически значения корреляционной и взаимной функций входа и выхода X (s) и Y (t) по реализациям этих случайных функций также подсчитывают на цифровых вычислительных машинах. [ 10 ]

Для того, чтобы быть уверенным в том, что в результате примененияметода Гаусса-Зейделя или метода наискорейшего спуска получен глобальный, а не локальный минимум целевой функции, приходится неоднократно повторять процедуру поиска, начиная его из различных начальных точек в пространстве параметров. [ 11 ]

Одним из самых распространенных итерационных методов, отличающийся простотой и легкостью программирования, являетсяметод Гаусса-Зейделя. [ 12 ]

14. В чем состоит сущность метода наискорейшего спуска?

В этом методе функция минимизируется по направлению, в котором она быстрее всего убывает, т.е. в направлении, обратном 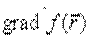. Вдоль этого направления функция зависит от одной параметрической переменной t, для нахождения минимума которой можно воспользоваться любым известным методом поиска минимума функции одной переменной. Спуск из точки начального приближения 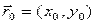против градиента до минимума t определяет новую точку 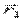, в которой вновь определяется градиент и делается следующий спуск. Условием окончания процесса, как и в случае координатного спуска, будет .

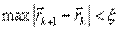С помощью метода градиентного спуска минимум гладких функций в общем случае находится быстрее, чем при использовании координатного спуска, однако нахождение градиента численными методами может свести на нет полученный выигрыш. Сходимость плохая для функций с овражным рельефом, т.е. с точки зрения сходимости градиентный спуск не лучше спуска по координатам.

Каждый спуск заканчивается в точке, где линия градиента касательна к линии (поверхности) уровня. Это означает, что каждый следующий спуск должен быть перпендикулярен предыдущему. Таким образом, вместо поиска градиента в каждой новой точке можно сосчитать градиент в начальной точке, и развернуть оси координат так, чтобы одна их осей была параллельна градиенту, а затем осуществлять спуск координатным методом.

15. В чем состоят достоинства и недостатки метода наискорейшего спуска?

Метод наискорейшего спуска требует решения на каждом шаге задачи одномерной оптимизации. Практика показывает, что этот метод часто требует меньшего числа операций, чем градиентный метод с постоянным шагом.

В общей ситуации, тем не менее, теоретическая скорость сходимости метода наискорейшего спуска не выше скорости сходимости градиентного метода с постоянным (оптимальным) шагом.

16. В чем состоит сущность градиентного метода с постоянным шагом?

В градиентном методе с постоянным шагом исходными данными являются требуемая точность e, начальная точка поиска Х⁰ и шаг поиска h.

Получение новых точек производится по формуле:

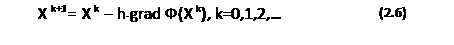
Формула (2.7) применяется, если для функции Ф(Х) необходимо найти минимум. Если же задача параметрической оптимизации ставится как задача поиска максимума, то для получения новых точек в градиентном методе с постоянным шагом используется формула:

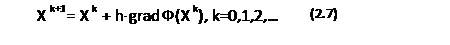
Каждая из формул (2.6), (2.7) является векторным соотношением, включающим n уравнений. Например, с учетом Х^k+1 = (x1^k+1, x2. ^k+1,…,xn^k+1), Х^k = (x1^k, x2. ^k,…,xn^k) формула (2.6) примет вид:

(2.8)

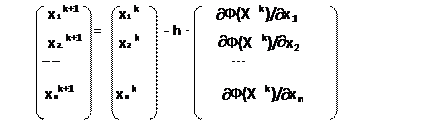
или в скалярном виде

В общем виде (2.9) можно записать:

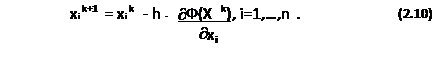
В качестве условия прекращения поиска во всех градиентных методах используется, как правило, комбинация двух условий: ç Ф(X^k+1) - Ф(X ^k) ç £ e или

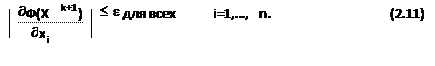
В градиентном методе можно несколько сократить число итераций, если научиться избегать ситуаций, когда несколько шагов поиска выполняются в одном и том же направлении.

17. В состоят достоинства и недостатки градиентного метода с постоянным шагом?

Из полученных результатов можно сделать вывод, что при слишком большом чаге метод расходится, при слишком малом сходится медленно и точчность хуже. Надо выбирать шаг наибольшим из тех, при которых метод сходится.

18. В чем состоит сущность метода Хука – Дживса?

На разработку методов прямого поиска для определения минимума функций и переменных было затрачено много усилий. Методы прямого поиска являются методами, в которых используются только значения функции. Мы рассмотрим подробно лишь один из них. Практика показала, что этот метод эффективен и применим для широкого числа приложений.
Рассмотрим функцию двух переменных. Ее линии постоянного уровня на рис. 1,

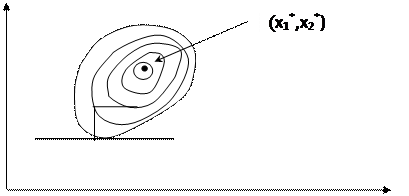
x₂

C D

A B

x₁

рис. 1

а минимум лежит в точке (x₁^*,x₂^*)[1]. Простейшим методом поиска является метод покоординатного спуска. Из точки А мы производим поиск минимума вдоль направления оси и, таким образом, находим точку В, в которой касательная к линии постоянного уровня параллельна оси. Затем, производя поиск из точки В направлении оси, получаем точку С, производя поиск параллельно оси, получаем точку D, и т. д. Таким образом, мы приходим к оптимальной точке. Очевидным образом эту идею можно применить для функций n-переменных.

Теоретически данный метод эффективен в случае единственного минимума функции. Но на практике он оказывается слишком медленным. Поэтому были разработаны более сложные методы, использующие больше информации на основании уже полученных значений функции.

Метод Хука-Дживса был разработан в 1961 году, но до сих пор является весьма эффективным и оригинальным. Поиск состоит из последовательности шагов исследующего поиска вокруг базисной точки, за которой в случае успеха следует поиск по образцу. Он применяется для решения задачи минимизирования функции без учета ограничений.

Описание этой процедуры представлено ниже:

А. Выбрать начальную базисную точку b₁ и шаг длиной h₁ для каждой переменной x _j, j = 1, 2,…, n. В приведенной ниже программе для каждой переменной используется шаг h, однако указанная выше модификация тоже может оказаться полезной.

Б. Вычислить f (х) в базисной точке b₁ с целью получения сведений о локальном поведении функции f (x). Эти сведения будут использоваться для нахождения подходящего направления поиска по образцу, с помощью которого можно надеяться достичь большего убывания значения функции. Функция f (x) в базисной точке b₁, находится следующим образом:

1. Вычисляется значение функции f (b₁) в базисной точке b₁.

2. Каждая переменная по очереди изменяется прибавлением длины шага. Таким образом, мы вычисляем значение функции f (b₁+h₁e₁), где e₁ – единичный вектор в направлении оси x₁. Если это приводит к уменьшению значения функции, то b₁ заменяется на b₁+h₁e₁. В противном случае вычисляется значение функции f (b₁-h­₁e₁), и если ее значение уменьшилось, то b₁ заменяем на b₁-h₁e₁. Если ни один из проделанных шагов не приводит к уменьшению значения функции, то точка b­₁ остается неизменной и рассматриваются изменения в направлении оси х₂, т. е. находится значение функции f (b₁+h₂e₂) и т. д. Когда будут рассмотрены все n переменные, мы будем иметь новую базисную точку b₂.

3. Если b₂=b₁, т. е. уменьшение функции не было достигнуто, то исследование повторяется вокруг той же базисной точки b₁, но с уменьшенной длиной шага. На практике удовлетворительным является уменьшение шага (шагов) в десять раз от начальной длины.

4. Если b₂ 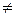b₁, то производится поиск по образцу.

В. При поиске по образцу используется информация, полученная в процессе исследования, и минимизация функции завершается поиском в направлении, заданном образцом. Эта процедура производится следующим образом:

1. Разумно двигаться из базисной точки b₂ в направлении b₂-b­₁, поскольку поиск в этом направлении уже привел к уменьшению значения функции. Поэтому вычислим функцию в точке образца

P₁=b₁+2(b₂-b₁).

В общем случае

P_i=b_i+2(b_i+1-b_i).

2. Затем исследование следует продолжать вокруг точки Р₁ (Р_i).

3. Если наименьшее значение на шаге В, 2 меньше значения в базисной точке b₂ (в общем случае b_i+1), то получают новую базисную точку b₃ (b_i+2), после чего следует повторить шаг В, 1. В противном случае не производить поиск по образцу из точки b₂ (b_i+1), а продолжить исследования в точке b₂ (b_i+1).

Г. Завершить этот процесс, когда длина шага (длины шагов) будет уменьшена до заданного малого значения.

Алгоритм метода.

1. Определить начальную точку x⁽⁰⁾, приращения по координатным направлениям D_i, i=1,...,N, коэффициент уменьшения шага a>1 и параметр окончания поиска e.

2. Провести исследующий поиск.

3. Проверка успешности исследующего поиска. Если успешно, перейти к шагу 5, если нет, продолжать поиск.

4. Проверка на окончание поиска:

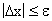
Если условие выполняется, поиск прекратить, если не выполняется, уменьшить шаг Dи перейти к шагу 2.

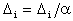
5. Провести поиск по образцу, то есть найти точку

x_p^(k+1) = x^(k)+(x^(k)-x^(k-1))

6. Провести исследующий поиск из точки x_p^(k+1) и получить точку x^(k+1).

7. Если f(x^(k+1)) < f(x^(k)),

то: x^(k-1) = x^(k);

x^(k) = x^(k+1);

goto 5.

иначе, goto 4.

19. В чем состоят достоинства и недостатки метода Хука – Дживса?

Достоинства метода: простая стратегия поиска, вычисление только значений функции, небольшой объём требуемой памяти.

Недостатки: алгоритм основан на циклическом движении по координатам. Это может привести к вырождению алгоритма в бесконечную последовательность исследующих поисков без поиска по образцу.

20. Как связаны между собой одномерные и многомерные методы оптимизации?

21. В чем состоит сущность метода Нелдера-Мида?

Метод Нелдера — Мида, также известный как метод деформируемого многогранника и симплекс-метод, — метод безусловной оптимизации функции от нескольких переменных, не использующий производной (точнее — градиентов) функции, а поэтому легко применим к негладким и/или зашумлённым функциям.

Суть метода заключается в последовательном перемещении и деформировании симплекса вокруг точки экстремума.

Метод находит локальный экстремум и может «застрять» в одном из них. Если всё же требуется найти глобальный экстремум, можно пробовать выбирать другой начальный симплекс. Более развитый подход к исключению локальных экстремумов предлагается в алгоритмах, основанных на методе Монте-Карло, а также вэволюционных алгоритмах.

22. В чем состоят достоинства и недостатки метода Нелдера-Мида?

метод Нелдера-Мида является очень эффективным алгоритмом поиска экстремума функции многих переменных, не накладывающим ограничений на гладкость функции. На каждой итерации алгоритма производится как правило одно-два вычисления значений функции, что чрезвычайно эффективно если эти вычисления очень медленны. Кроме того, алгоритма очень прост в реализации. Главным же его недостатком является отсутствие теории сходимости и наличие примеров, когда метод расходится даже на гладких функциях.

23. Из каких операций строится метод Нелдера-Мида?

Инициализация. Произвольным образом выбирается 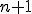точка 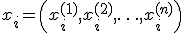, образующие симплекс n-мерного пространства. В этих точках вычисляются значения функции: .

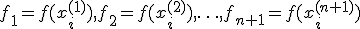1. Сортировка. Из вершин симплекса выбираем три точки: 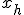с наибольшим (из выбранных) значением функции 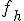, 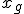со следующим по величине значением 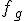и 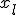с наименьшим значением функции 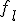. Целью дальнейших манипуляций будет уменьшение по крайней мере .

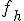2. Найдём центр тяжести всех точек, за исключением 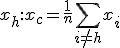. Вычислять 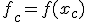не обязательно.

3. Отражение. Отразим точку 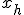относительно 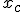с коэффициентом 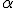(при 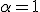это будет центральная симметрия, в общем случае — гомотетия), получим точку 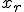и вычислим в ней функцию: 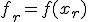. Координаты новой точки вычисляются по формуле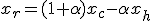

4. Далее сравниваем значение 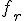со значениями :

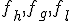4а. Если 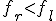, то производим растяжение. Новая точка 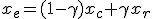и значение функции .

Если 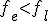, то заменяем точку 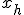на 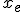и заканчиваем итерацию (на шаг 8).

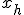Если , то заменяем точку на 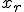и заканчиваем итерацию (на шаг 8).

4b. Если 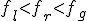, то заменяем точку 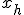на 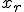и переходим на шаг 8.

4с. Если 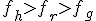, то меняем обозначения 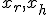(и соответствующие значения функции) местами и переходим на шаг 5.

4d. Если 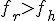, то переходим на шаг 5.

5. Сжатие. Строим точку 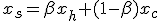и вычисляем в ней значение .

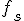6. Если 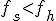, то заменяем точку 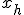на 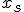и переходим на шаг 8.

7. Если 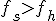, то производим сжатие симплекса — гомотетию к точке с наименьшим значением 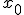: для всех требуемых точек .

8. Последний шаг — проверка сходимости. Может выполняться по-разному, например, оценкой дисперсии набора точек. Суть проверки заключается в том, чтобы проверить взаимную близость полученных вершин симплекса, что предполагает и близость их к искомому минимуму. Если требуемая точность ещё не достигнута, можно продолжить итерации с шага 1.

24. Что такое «симплекс»?

Симплекс или n -мерный тетраэдр (от лат. simplex — простой) — геометрическая фигура, являющаяся n -мерным обобщением треугольника.

26. В чем состоят достоинства и недостатки прямых методов оптимизации (методов нулевого порядка)? Приведите и кратко опишите известные Вам методы нулевого порядка.

Методы поиска экстремума классифицируются по следующим признакам: в зависимости от характера экстремума существуют методы условной и безусловной, локальной и глобальной оптимизации; по числу переменных проектирования различают методы одномерного и многомерного поиска, а по характеру информации о виде целевой функции - методы нулевого, первого и второго порядков, причем в методах первого порядка используют градиент целевой функции, поэтому эти методы называются градиентными, в методах второго порядка применяют вторые производные, а вметодах нулевого порядка производные не используют. [ 9 ]

Познание у Аристотеля имеет своим предметом бытие. Основа опыта — в ощущениях, памяти и привычке. Любое знание начинается с ощущений: оно есть то, что способно принимать форму чувственно воспринимаемых предметов без их материи; разум же усматривает общее в единичном.

Однако с помощью одних только ощущений и восприятий приобрести научное знание нельзя, потому что все вещи имеют изменчивый и переходящий характер. Формами истинно научного знания являются понятия, постигающие сущность вещи.

Детально и глубоко разобрав теорию познания, Аристотель создал труд по логике, который сохраняет своё непреходящее значение и поныне. Здесь он разработал теорию мышления и его формы, понятия, суждения и умозаключения.

Аристотель является и основоположником логики.

Задача понятия состоит в восхождении от простого чувственного восприятия к вершинам абстракции. Научное знание есть знание наиболее достоверное, логически доказуемое и необходимое.

В учении о познании и его видах Аристотель различал «диалектическое» и «аподиктическое» познание. Область первого — «мнение», получаемое из опыта, второго — достоверное знание. Хотя мнение и может получить весьма высокую степень вероятности по своему содержанию, опыт не является, по Аристотелю, последней инстанцией достоверности знания, ибо высшие принципы знания созерцаются умом непосредственно.

Отправным пунктом познания являются ощущения, получаемые в результате воздействия внешнего мира на органы чувств, без ощущений нет знаний. Отстаивая это теоретико-познавательное основное положение, «Аристотель вплотную подходит к материализму». Ощущения Аристотель правильно считал надежными, достоверными свидетельствами о вещах, но оговариваясь добавлял, что сами по себе ощущения обуславливают лишь первую и самую низшую ступень познания, а на высшую ступень человек поднимается благодаря обобщению в мышлении общественной практики.

Цель науки Аристотель видел в полном определении предмета, достигаемом только путем соединения дедукции и индукции:

1) знание о каждом отдельном свойстве должно быть приобретено из опыта;

2) убеждение в том, что это свойство — существенное, должно быть доказано умозаключением особой логической формы — категорическим силлогизмом.

Исследование категорического силлогизма, осуществленное Аристотелем в «Аналитике», стало наряду с учением о доказательстве центральной частью его логического учения.

Основной принцип силлогизма выражает связь между родом, видом и единичной вещью. Эти три термина понимались Аристотелем как отражение связи между следствием, причиной и носителем причины.

Система научных знаний не может быть сведена к единой системе понятий, ибо не существует такого понятия, которое могло бы быть предикатом всех других понятий: поэтому для Аристотеля оказалось необходимым указать все высшие роды, а именно категории, к которым сводятся остальные роды сущего.

Размышляя над категориями и оперируя ими в анализе философских проблем, Аристотель рассматривал и операции ума и его логику, и, в том числе, логику высказываний. Разрабатывал Аристотель и проблемы диалога, углубившие идеи Сократа.

Он сформулировал логические законы:

· закон тождества — понятие должно употребляться в одном и том же значении в ходе рассуждений;

· закон противоречия — «не противоречь сам себе»;

· закон исключенного третьего — «А или не-А истинно, третьего не дано».

Аристотель разрабатывал учение о силлогизмах, в котором рассматриваются всевозможные виды умозаключений в процессе рассуждений.

3. «Здесь и сейчас!» - главная заповедь морального человека. – Как вы это объясните?

4. Каковы специфика и источник философских проблем? – Сформулируйте несколько важных для вас философских проблем и проследите их происхождение.

Основные проблемы философии:

— объекта и предмета философии (объект — мир как единое целое; предмет — законы, свойства и формы бытия, которые действуют во всех областях материального мира, во всех предметах, процессах, явлениях, так как они связаны в неразрывном единстве);

— первоосновы мира (первая сторона главного назначения философии);

— развития мира (диалектический и метафизический способы познания);

— познания мира (определение объекта и субъекта познания, решение проблемы истины, роли практики);

— человека и его места в мире (изучение мироздания, развития человеческой культуры).

Дата добавления: 2015-04-24