Вращательное движение, угловая скорость, угловое ускорение

Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.

Для описания вращательного движения тела вокруг неподвижной оси можно использовать только угловые параметры. угол поворота тела, рад; со — угловая скорость, определяет изменение угла поворота в единицу времени единицы измерения- рад/с.

Изменение угловой скорости во времени определяется угловым ускорением. Частные случаи вращательного движения. Уравнение (закон) равномерного вращения в данном случае имеет вид: 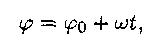угол поворота до начала отсчета.

Уравнение (закон) равнопеременного вращения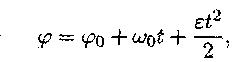

начальная угловая скорость. Угловое ускорение при ускоренном движении — величина положительная; угловая скорость будет все время возрастать. Угловое ускорение при замедленном движении — величина отрицательная; угловая скорость убывает.

Углова́я ско́рость — векторная величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

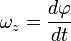, а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону.

Единица измерения угловой скорости, принятая в системах - радианы в секунду. В технике также используются обороты в секунду, намного реже — градусы в секунду, грады в секунду.

Вектор (мгновенной) скорости любой точки (абсолютно) твердого тела, вращающегося с угловой скоростью 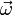определяется формулой:

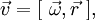где 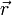— радиус-вектор к данной точке из начала координат, расположенного на оси вращения тела, а квадратными скобками обозначено векторное произведение. Линейную скорость (совпадающую с модулем вектора скорости) точки на определенном расстоянии (радиусе) r от оси вращения можно считать так: v = r ω. Если вместо радианов применять другие единицы углов, то в двух последних формулах появится множитель, не равный единице.

Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.

При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно:

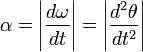
Вектор углового ускорения α направлен вдоль оси вращения (в сторону 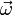при ускоренном вращении и противоположно 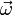— при замедленном).

При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости ω по времени, то есть

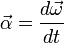, и направлен по касательной к годографу вектора 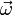в соответствующей его точке.

Существует связь между тангенциальным и угловым ускорениями:

a _τ = α R,

где R — радиус кривизны траектории точки в данный момент времени. Итак, угловое ускорение равно второй производной от угла поворота по времени или первой производной от угловой скорости по времени. Угловое ускорение измеряется в рад/сек².

Дата добавления: 2015-04-24