Уравнение движения твердого тела

Центр масс системы материальных точек.

Введем важное понятие центра масс СМТ.

Рассмотрим выражение для импульса СМТ

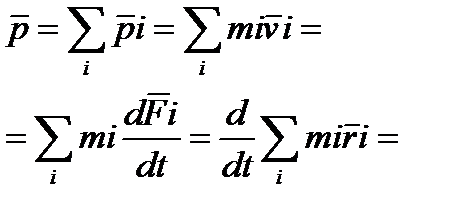
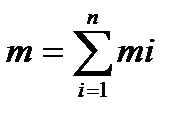(1), где m – центр масс

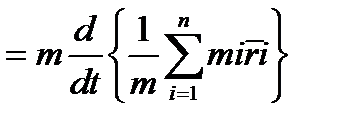
Вектор 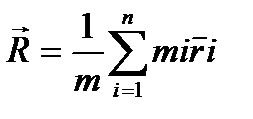(2)

Радиусом вектором центра масс. Иногда называют центром инерции.

Очевидно 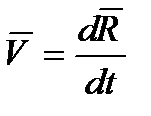(3) - вектор скорости центра масс СМТ.

Центр масс - это фиктивная точка которая сосредотачивает в себе всю массу СМТ.

Положение точки задается формулой(2).С учетом определения последняя формула преобразуется следующим образом 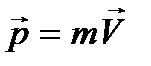(4).

Импульс всей СМТ = импульсу центра масс. Эквивалентный вид 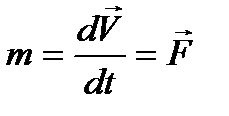(5)

Ур-е движения для импульса СМТ эквивалентно ур-ю движения МТ вся масса, которой сосредоточена в центре. А все внешние силы, действующие на СМТ, приложены к ее центру масс. Это утверждение называется теоремой о движении центра масс.

Мы говорили о том, что TT есть СМТ и эта система обладает 6 степенями свободы, поэтому для описания СМТ необходимо 6 скалярных уравнений;

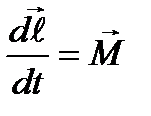
Эти уравнения есть уравнения описывающие динамику ТТ – это 6 скалярных уравнений. Уравнения моментов можно брать относительно произвольного неподвижного начала или относительно центра масс ТТ. Можно также брать произвольно движ. начало, если только скорость его в любой момент времени параллельна скорости центра масс. При ограничение свободы движ. число независимых уравнений, требующихся для описания движ. ТТ, уменьшается. Она всегда равна числу степеней свободы. Внутренние силы не влияют на движ. ТТ.

Дата добавления: 2015-04-24