Первое и второе начала термодинамики для элементарного процесса. Второе начало термодинамики в формулировке Клаузиуса

Энтропия.

Второе начало термодинамики в формулировке Клаузиуса

Уравнение политропы и адиабаты для идеального газа.

Уравнение адиабатического процесса.

Уравнение адиабатического процесса (C=0):

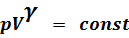(1)

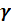– показатель адиабата

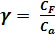(2)

Уравнение политропического процесса имеет след. вид:

C=const;

pVⁿ = const (1)

n – показатель политропности

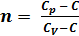(2)

Уравнение адиабатического процесса:

C=0

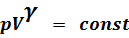(1)

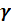– показатель адиабата

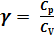(2)

Энтропия – это ф-я состояния ТДС, которая определяется след. образом:

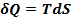(1)

Ф-я состояния ТДС, определяемая с помощью дифференциального соотношения 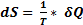(2) наз-ся энтропией.

Элементарный процесс – передача энергии системе, связанной с бесконечным изменением её внутренних и внешних параметров.

Элементарный процесс записывается след. образом:

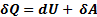(1) – это закон сохранения энергии

Закон сохранения энергии (1) – это первое начало термодинамики для элементарного процесса.

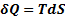
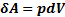
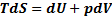(2) – объединяет 1 и 2 начало.

Уравнение (2), объединяющее 1 и 2 начало ТД наз-ся основным уравнением термодинамики для равновесных ТД процессов.

44. Термодинамический потенциал – внутренняя энергия U(S,V).

Все термодинамические потенциалы выводятся из первого и второго начал ТД.

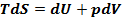(1)

Первый потенциал внутренняя энергия U.

Пусть нам известна ф-я:

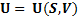(2)

Из (1) следует, что:

(3)

_V (4)

_s (5)

Внутренняя энергия U в переменных S и V, наз-ся ТД-им потенциалом.

45. Термодинамический потенциал – свободная энергия U(S,V).

U, как потенциал не удобен, т.к. он содержит S. Следовательно так, что было dT, dV.

Left = TdS – d(TS) = TdS – dT*S – TdS = -SdT

Right = dU + pdV – d(TS) = d(U - TS) + pdV

Введём новую ф-ю F:

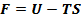(1)

Приравниваем правую часть:

-SdT = dF + pdV

переносим:

dF = -SdT – pdV (2)

найдём S:

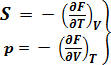(3)

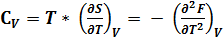(4)

Ф-я F = от F(t), также является термодинамическим и наз-ся свободной энергией.

46. Термодинамический потенциал – потенциал Гиббса U(S,V).

Переменные Т и р:

Добавим к обеим частям формулы dF = -SdT – pdV (1) + d(pV)

Получим:

d(F + pV) = -SdT – Vdp (2)

Введём новую ф-ю Ф:

Ф = F + pV (3)

Дата добавления: 2015-04-24