Энтропия. Энтропия и термодинамическая вероятность. Формула Больцмана. Статистический смысл второго начала. Третье начало термодинамики

Термодинамическая энтропия — функция состояния термодинамической системы. Максимальное значение энтропии достигается тогда, когда система приходит в равновесное состояние.

Термодинамическая вероятность(или статический вес) — число способов, которыми может быть реализовано состояние физической системы. В термодинамике состояние физической системы характеризуется определёнными значениями плотности, давления, температуры и др. измеримых величин.

Связь между термодинамической вероятностью состояния системы и ее энтропией была установлена в 1875 г. двумя знаменитыми учеными – Д. Гиббсом и Л. Больцманом. Эта связь выражается формулой Больцмана, которая имеет вид:

,

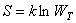где , R – универсальная газовая постоянная, N_A – число Авогадро. О логарифмической зависимости между энтропией и термодинамической вероятностью можно сделать вывод на основе следующих соображений. Из определения энтропии ясно, что энтропия любого вещества пропорциональна массе. Это значит, что энтропия всей системы равна сумме энтропий ее отдельных частей. Разделим вещество на две части, тогда, очевидно, что

.

По законам теории вероятности вероятность данного состояния всей массы вещества равна произведению вероятностей состояния его отдельных частей, то есть

.

Таким образом, суммированию энтропий соответствует умножение термодинамических вероятностей отдельных частей. Из всех математических функций такими свойствами обладает только логарифмическая функция.

С точки зрения статистической термодинамики второе начало термодинамики можно сформулировать следующим образом: Система стремится самопроизвольно перейти в состояние с максимальной термодинамической вероятностью. Статистическое толкование второго начала термодинамики придает энтропии конкретный физический смысл меры термодинамической вероятности состояния системы.

Дата добавления: 2015-04-24