Момент инерции шара

Момент инерции однородного тела вращения. Моменты инерции конуса, шара.

Линия 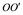- ось вращения.

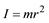- масса на квадрат радиуса окружности, по которой движется материальная точка.

Все тело мысленно разбиваем на маленькие объемы. Масса этого кусочка .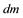

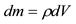
Твердое тело представляется как совокупность системы точечных масс.

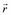- расстояние, на котором находится точка от оси вращения.

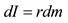
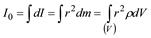- общий алгоритм определения собственного момента инерции твердого тела, относительно оси проходящей через центр инерции данного тела.

Сплошной шар массы m и радиуса R можно рассматривать как совокупность бесконечно тонких сферических слоев с массами dm, радиусом r, толщиной dr (рис.35).

Рассмотрим малый элемент сферического слоя $\delta$ m с координатами x, y, z. Его моменты инерции относительно осей проходящих через центр слоя - $\delta$ J_x, $\delta$ J_y, $\delta$ J_z, равны

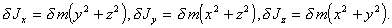
Т. е. можно записать 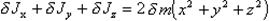(п.26)

Так как для элементов сферического слоя x²+y²+z²=r² то

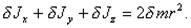
После интегрирования по всему объему слоя получим 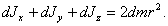(п.27)

Так как, в силу симметрии для сферического слоя dJ_x=dJ_y=dJ_z=dJ, а 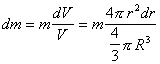, то 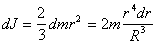Интегрируя по всему объему шара, получаем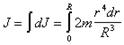
Окончательно (после интегрирования) получим, что момент инерции шара относительно оси, проходящей через его центр равен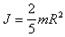

Разобьём КОНУС на цилиндрические слои ось толщиной dr. Масса такого слоя dm = rp r ² dr,

где ρ – плотность материала, из которого изготовлен конус. Момент инерции этого слоя dI = dm^.r ².

Момент инерции всего конуса складывается из моментов инерции всех слоёв:

I = 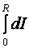= 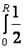ρπ r ⁴ dr = 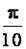ρ R ⁵.

Остаётся выразить его через массу всего цилиндра: m = 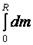= = 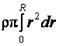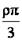R ³,

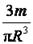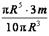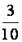отсюда ρ = , I = = mR ².

18. Кинетическая энергия вращающегося твёрдого тела вокруг закреплённой оси. Кинетическая энергия твёрдого тела при плоском движении.

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Единица измерения в системе СИ — Джоуль. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

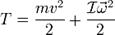
19. Уравнения динамики твёрдого тела. Центр тяжести. Условия равновесия твёрдого тела.

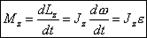- уравнение динамики вращательного движения твердого тела относительно неподвижной оси z, где M_z – момент силы, L_z – момент импульса, J_z – момент инерции тела относительно оси z, 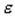- угловое ускорение. F=ma

Центром тяжести тела называется точка, относительно которой суммарный момент сил тяжести, действующих на систему, равен нулю. Например, в системе, состоящей из 2 одинаковых масс, соединённых несгибаемым стержнем и помещённой в неоднородное гравитационное поле (например, планеты), центр масс будет находиться в середине стержня, в то время как центр тяжести будет смещён к тому концу стержня, который находится ближе к планете (ибо вес массы P = m·g зависит от гравитационного поля g), и, вообще говоря, даже расположен вне стержня. В постоянном параллельном (однородном) гравитационном поле центр тяжести всегда совпадает с центром масс. Поэтому на практике эти два центра почти совпадают (так как гравитационное поле в некосмических задачах может считаться постоянным в объёме тела).

По этой же причине понятия центр масс и центр тяжести совпадают при использовании этих терминов в геометрии, статистике и тому подобных областях, где применение его по сравнению с физикой можно назвать метафорическим и где неявно предполагается ситуация их эквивалентности (так как реального гравитационного поля нет и не имеет смысла учёт его неоднородности). В этих применениях традиционно оба термина синонимичны, и нередко второй предпочитается просто в силу того, что он более старый

Механическое равновесие - состояние системы, при котором сумма всех сил, действующих на каждую её частицу, равна нулю и алгебраическая сумма моментов всех сил, приложенных к телу относительно оси вращения, проходящей через любую точку O, равна нулю ΣΜO(Fί)=0. Такое определение ограничивает как поступательное движение тела, так и вращательное.

Виды равновесия:

Приведём пример для системы с одной степенью свободы. В этом случае достаточным условием положения равновесия будет являться наличие локального экстремума в исследуемой точке. Как известно, условием локального экстремума дифференцируемой функции является равенство нулю её первой производной. Чтобы определить, когда эта точка является минимумом или максимумом, необходимо проанализировать её вторую производную. Устойчивость положения равновесия характеризуется следующими вариантами:

Дата добавления: 2015-04-24