Виды степенных средних. Правило мажорантности

Степенные средние делятся на простые и взвешенные.

Общая формула простой степенной средней записывается следующим образом: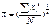

Взвешанная:

где k-показатель степени, определяющий вид степенной средней, f_i-вес усреднения

При k = 1 – средняя арифметическая;

k = 2 – средняя квадратическая;

k = 3 – средняя кубическая;

k = 0 – средняя геометрическая;

k = -1 – средняя гармоническая.

Средняя квадратическая величина применяется тогда, когда вместо индивидуальных значений признака представлены квадраты исходных величин.

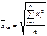
Средняя кубическая если необх.сохр. неизменной сумму кубов индивидуальных значений признака при их замене на сред.величину

Средняя геометрическая применяется в случаях определения средней по значениям, имеющим большой разброс, либо в случаях определения средней величины по относительным показателям.

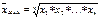
Средняя гармоническая – это величина, обратная средней арифметической из обратных значений признака. Различают среднюю гармоническую простую и взвешенную.

Средняя гармоническая простая.

Средняя гармоническая взвешенная применяется тогда, когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение.

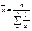
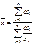
Правило мажорантности: чем выше показатель степени k, тем больше значение ср.величины при условии, что индивид.значение признака варьирует.

Хгарм < Хгеом < Харифм < Хкв < Хкуб

Дата добавления: 2015-04-24