
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод корреляционных полей
|
|
|
|
Метод корреляционных таблиц.
Метод групповых таблиц.
Групповыми называются таблицы, имеющие в подлежащем группировку единиц совокупности по одному признаку.
| Распределение населения России по полу на 1 января 2007 г. | ||
| млн.чел | в % к итогу | |
| Численность населения — всего | 142,0 | 100,0 |
| В том числе: | ||
| Мужчины | 65,8 | 46,3 |
| Женщины | 76,4 | 53,7 |
Корреляционный анализ — это количественный метод определения тесноты и направления взаимосвязи между выборочными переменными величинами.
Линейная корреляция:
Данная корреляция характеризует линейную взаимосвязь в вариациях переменных. Она может быть парной (две коррелирующие переменные) или множественной (более двух переменных), прямой или обратной — положительной или отрицательной, когда переменные варьируют соответственно в одинаковых или разных направлениях.
Если переменные — количественные и равноценные в своих независимых наблюдениях 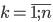 при их общем количестве
при их общем количестве 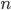 , то важнейшими эмпирическими мерами тесноты их линейной взаимосвязи являются коэффициент прямой корреляции знаков австрийского психолога Г.Т.Фехнера (1801-1887) и коэффициенты парной, чистой (частной) и множественной (совокупной) корреляции английского статистика-биометрика К.Пирсона (1857-1936).
, то важнейшими эмпирическими мерами тесноты их линейной взаимосвязи являются коэффициент прямой корреляции знаков австрийского психолога Г.Т.Фехнера (1801-1887) и коэффициенты парной, чистой (частной) и множественной (совокупной) корреляции английского статистика-биометрика К.Пирсона (1857-1936).
Коэффициент парной корреляции знаков Фехнера определяет согласованность направлений в индивидуальных отклонениях переменных 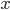 и
и 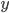 от своих средних
от своих средних 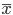 и
и 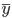 . Он равен отношению разности сумм совпадающих (
. Он равен отношению разности сумм совпадающих (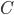 ) и несовпадающих (
) и несовпадающих (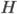 ) пар знаков в отклонениях
) пар знаков в отклонениях 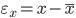 и
и 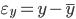 к сумме этих сумм:
к сумме этих сумм:
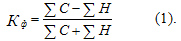
Величина Кф изменяется от -1 до +1. Суммирование в (1) производится по наблюдениям 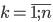 , которые не указаны в суммах ради упрощения. Если какое-то одно отклонение
, которые не указаны в суммах ради упрощения. Если какое-то одно отклонение 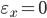 или
или 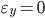 , то оно не входит в расчет. Если же сразу оба отклонения нулевые:
, то оно не входит в расчет. Если же сразу оба отклонения нулевые: 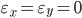 , то такой случай считается совпадающим по знакам и входит в состав
, то такой случай считается совпадающим по знакам и входит в состав 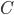 . В таблице 12.1. показана подготовка данных для расчета (1).
. В таблице 12.1. показана подготовка данных для расчета (1).
Таблица 12.1 Данные для расчета коэффициента Фехнера.
| Магазин | Число работников, тыс. чел. | Товарооборот, у.е. | Отклонение от средних
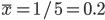 и и 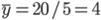
| Сравнение знаков 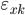 и и 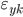
| ||
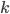
| 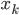
| 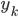
| 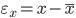
| 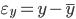
| совпа-дение (Ск) | несов-падение (Нк) |
| 0,2 | 3,1 | +0,0 | -0,9 | |||
| 0,1 | 3,1 | -0,1 | -0,9 | |||
| 0,4 | 5,0 | +0,2 | +1,0 | |||
| 0,2 | 4,4 | +0,0 | +0,4 | |||
| 0,1 | 4,4 | -0,1 | +0,4 | |||
| Итого | 1,0 | 20,0 | - | - |
По (1) имеем Кф = (3 — 2)/(3 + 2) = 0,20. Направление взаимосвязи в вариациях!!Средняя численность работников|численности работников]] и объема товарооборота — положительное (прямолинейное): знаки в отклонениях и 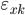 и
и 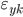 в своем большинстве (в 3 случаях из 5) совпадают между собой. Теснота взаимосвязи переменных по шкале Чеддока — слабая.
в своем большинстве (в 3 случаях из 5) совпадают между собой. Теснота взаимосвязи переменных по шкале Чеддока — слабая.
Коэффициенты парной, чистой (частной) и множественной (совокупной) линейной корреляции Пирсона, в отличие от коэффициента Фехнера, учитывают не только знаки, но и величины отклонений переменных. Для их расчета используют разные методы. Так, согласно методу прямого счета по несгруппированным данным, коэффициент парной корреляции Пирсона имеет вид:
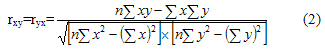
Этот коэффициент также изменяется от -1 до +1. При наличии нескольких переменных рассчитывается коэффициент множественной (совокупной) линейной корреляции Пирсона. Для трех переменных x, y, z он имеет вид
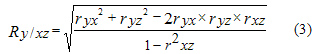
Этот коэффициент изменяется от 0 до 1. Если элиминировать (совсем исключить или зафиксировать на постоянном уровне) влияние 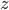 на
на 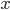 и
и 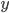 , то их "общая" связь превратится в "чистую", образуя чистый (частный) коэффициент линейной корреляции Пирсона:
, то их "общая" связь превратится в "чистую", образуя чистый (частный) коэффициент линейной корреляции Пирсона:
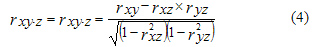
Этот коэффициент изменяется от -1 до +1. Квадраты коэффициентов корреляции (2)-(4) называются коэффициентами (индексами) детерминации — соответственно парной, чистой (частной), множественной (совокупной):
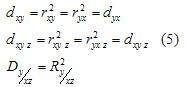
Каждый из коэффициентов детерминации изменяется от 0 до 1 и оценивает степень вариационной определенности в линейной взаимосвязи переменных, показывая долю вариации одной переменной (y), обусловленную вариацией другой (других) — x и y. Многомерный случай наличия более трех переменных здесь не рассматривается.
Согласно разработкам английского статистика Р.Э. Фишера (1890-1962), статистическая значимость парного и чистого (частного) коэффициентов корреляции Пирсона проверяется в случае нормальности их распределения, на основании 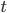 -распределения английского статистика В.С. Госсета (псевдоним "Стьюдент"; 1876-1937) с заданным уровнем вероятностной значимости
-распределения английского статистика В.С. Госсета (псевдоним "Стьюдент"; 1876-1937) с заданным уровнем вероятностной значимости  и имеющейся степени свободы
и имеющейся степени свободы 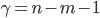 , где
, где 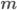 — число связей (факторных переменных). Для парного коэффициента
— число связей (факторных переменных). Для парного коэффициента 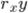 имеем его среднеквадратическую ошибку
имеем его среднеквадратическую ошибку 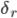 и фактическое значение
и фактическое значение 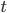 -критерия Стьюдента:
-критерия Стьюдента:
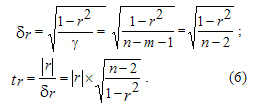
Для чистого коэффициента корреляции 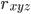 при расчете его
при расчете его 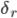 вместо (n-2) надо брать
вместо (n-2) надо брать 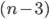 , т.к. в этом случае имеется m=2 (две факторные переменные x и z). При большом числе n>100 вместо (n-2) или (n-3) в (6) можно брать n, пренебрегая точностью расчета.
, т.к. в этом случае имеется m=2 (две факторные переменные x и z). При большом числе n>100 вместо (n-2) или (n-3) в (6) можно брать n, пренебрегая точностью расчета.
Если tr > tтабл., то коэффициент парной корреляции — общий или чистый является статистически значимым, а при tr ≤ tтабл. — незначимым.
Значимость коэффициента множественной корреляции R проверяется по F — критерию Фишера путем расчета его фактического значения
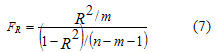
При FR > Fтабл. коэффициент R считается значимым с заданным уровнем значимости a и имеющихся степенях свободы 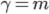 и
и 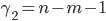 , а при Fr≤ Fтабл — незначимым.
, а при Fr≤ Fтабл — незначимым.
В совокупностях большого объема n > 100 для оценки значимости всех коэффициентов Пирсона вместо критериев t и F применяется непосредственно нормальный закон распределения (табулированная функция Лапласа-Шеппарда).
Наконец, если коэффициенты Пирсона не подчиняются нормальному закону, то в качестве критерия их значимости используется Z — критерий Фишера, который здесь не рассматривается.
Условный пример расчета (2) — (7)дан в табл. 12.2, где взяты исходные данные табл.12.1 с добавлением к ним третьей переменной z — размера общей площади магазина (в 100 кв. м).
Таблица 12.2. Подготовка данных для расчета коэффициентов корреляции Пирсона
| Мага-зин | Показатели | ||||||||
| к | xk | yk | zk | xkyk | xkzk | ykzk | |||
| 0,2 | 3,1 | 0,1 | 0,62 | 0,02 | 0,31 | 0,04 | 9,61 | 0,01 | |
| 0,1 | 3,1 | 0,1 | 0,31 | 0,01 | 0,31 | 0,01 | 9,61 | 0,01 | |
| 0,4 | 5,0 | 1,0 | 2,00 | 0,40 | 5,00 | 0,16 | 25,00 | 1,00 | |
| 0,2 | 4,4 | 0,2 | 0,88 | 0,04 | 0,88 | 0,04 | 19,36 | 0,04 | |
| 0,1 | 4,4 | 0,6 | 0,44 | 0,06 | 2,64 | 0,01 | 19,36 | 0,36 | |
| Итого | 1,0 | 20,0 | 2,0 | 4,25 | 0,53 | 9,14 | 0,26 | 82,94 | 1,42 |
Согласно (2) — (5), коэффициенты линейной корреляции Пирсона равны:
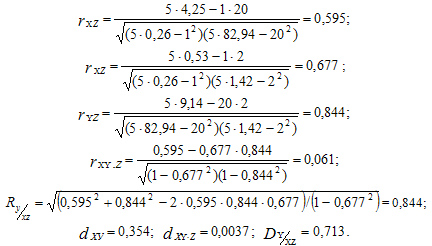
Взаимосвязь переменных x и y является положительной, но не тесной, составляя по их парному коэффициенту корреляции величину 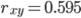 и по чистому — величину
и по чистому — величину 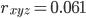 и оценивалась по шкале Чеддока соответственно как "заметная" и "слабая".
и оценивалась по шкале Чеддока соответственно как "заметная" и "слабая".
Коэффициенты детерминации dxy =0,354 и dxy.z = 0,0037 свидетельствуют, что вариация у (товарооборота) обусловлена линейной вариацией x (численности работников) на 35,4% в их общей взаимосвязи и в чистой взаимосвязи — только на 0,37%. Такое положение обусловлено значительным влиянием на x и y третьей переменной z — занимаемой магазинами общей площади. Теснота ее взаимосвязи с ними составляет соответственно rxz=0,677 и ryz=0,844.
Коэффициент множественной (совокупной) корреляции трех переменных показывает, что теснота линейной взаимосвязи x и z c y составляет величину R = 0,844, оцениваясь по шкале Чеддока как "высокая", а коэффициент множественный детерминации — величину D=0,713, свидетельствуя, что 71,3 % всей вариации у (товарооборота) обусловлены совокупным воздействием на нее переменных x и z. Остальные 28,7% обусловлены воздействием на y других факторов или же криволинейной связью переменных y, x, z.
Для оценки значимости коэффициентов корреляции возьмем уровень значимости 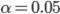 . По исходным данным имеем степени свободы
. По исходным данным имеем степени свободы 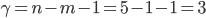 для
для 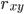 и
и 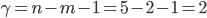 для
для 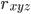 . По теоретической таблице находим соответственно tтабл.1. = 3,182 и tтабл.2. = 4,303. Для F-критерия имеем
. По теоретической таблице находим соответственно tтабл.1. = 3,182 и tтабл.2. = 4,303. Для F-критерия имеем 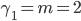 и
и 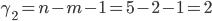 и по таблице находим Fтабл. = 19,0. Фактические значения каждого критерия по (6) и (7) равны:
и по таблице находим Fтабл. = 19,0. Фактические значения каждого критерия по (6) и (7) равны:
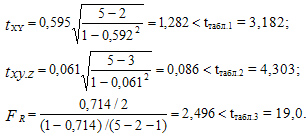
Все расчетные критерии меньше своих табличных значений: все коэффициенты корреляции Пирсона статистически незначимы.
Построение корреляционных полей - графическое изображение функций от фактора с целью предварительного определения тесноты и формы связи между функцией и каждым фактором.
Корреляционные поля построены по исходным статистическим данным X1 — Х4 (факторы) и Y (функция). Анализ корреляционных полей показывает, что:
· между Y и X4 теснота связи слабая, по форме она линейная, обратно пропорциональная;
· между Y и Х1 теснота связи высокая, по форме она линейная, прямо пропорциональная;
· между Y и Х3 связи нет, т.к. функцию Y = f(X3) можно провести в любом направлении;
· между Y и Х4 теснота связи высокая, форма связи — гиперболическая, после линии А—А фактор Х4 на Y уже не оказывает влияния.
Корреляционное поле и корреляционная таблица являются исходными данными при корреляционном анализе. Пусть 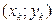 ,
, 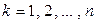 , – результаты парных наблюдений над случайными величинами Х и Y. Изображая полученные результаты в виде точек в декартовой системе координат, получим корреляционное поле. По характеру расположения точек поля можно составить предварительное представление о форме зависимости случайных величин (например, о том, что одна из них в среднем возрастает или убывает с возрастанием другой).
, – результаты парных наблюдений над случайными величинами Х и Y. Изображая полученные результаты в виде точек в декартовой системе координат, получим корреляционное поле. По характеру расположения точек поля можно составить предварительное представление о форме зависимости случайных величин (например, о том, что одна из них в среднем возрастает или убывает с возрастанием другой).
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 664; Нарушение авторских прав?; Мы поможем в написании вашей работы!