Вывод основного уравнения МКТ

Пусть имеется кубический сосуд с ребром длиной l и одна частица массой m в нём.

Обозначим скорость движения v_x, тогда перед столкновением со стенкой сосуда импульс частицы равен mv_x, а после — − mv_x, поэтому стенке передается импульс p = 2 mv_x. Время, через которое частица сталкивается с одной и той же стенкой, равно .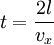

Отсюда следует:

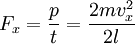
Так как давление 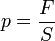, следовательно сила F = p * S

Подставив, получим:

Преобразовав: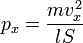

Так как рассматривается кубический сосуд, то V = Sl

Отсюда:

.

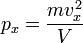Соответственно, 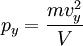и .

Таким образом, для большого числа частиц верно следующее: 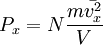, аналогично для осей y и z.

Поскольку 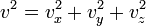, то 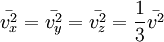. Это следует из того, что все направления движения молекул в хаотичной среде равновероятны.

Отсюда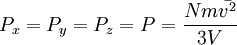

или .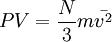

Пусть — среднее значение кинетической энергии всех молекул, тогда:

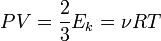, откуда .

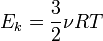Для одного моля выражение примет вид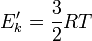

ия.

1. Дать определения и записать формулы для массы молекулы,

относительной молекулярной массы, молярной массы, количества вещества.

Указать физический смысл постоянной Авогадро

Молекуля́рная ма́сса (менее правильный термин: молекулярный вес) — масса молекулы, выраженная в атомных единицах массы. Численно равна молярной массе. Однако следует чётко представлять разницу между молярной массой и молекулярной массой, понимая, что они равны лишь численно и различаются по размерности.

Молекулярные массы сложных молекул можно определить, просто складывая молекулярные массы входящих в них элементов. Например, молекулярная масса воды (H₂O) есть

M _H2O = 2 M _H + M _O ≈ 2·1+16 = 18 а. е. м.

Число́ Авога́дро, конста́нта Авогадро — физическая константа, численно равная количеству специфицированных структурных единиц (атомов, молекул, ионов, электронов или любых других частиц) в 1 моле вещества. Определяется как количество атомов в 12 граммах (точно) чистого изотопа углерода-12. Обозначается обычно как N _A, реже как L ^[1].

Значение числа Авогадро:

N _A = 6,022 141 79(30)×10²³ моль⁻¹.

13. Дайте понятие и укажите свойства идеального газа. Запишите основное уравнение МКТ идеального газа и дайте его анализ.

Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями. Свойства идеального газа описываются уравнением Менделеева — Клапейрона

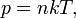
где 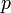— давление, 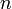— концентрация частиц, 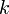— постоянная Больцмана, 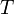— абсолютная температура.

Равновесное распределение частиц классического идеального газа по состояниям описывается распределением Больцмана:

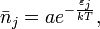
где 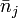— среднее число частиц, находящихся в 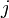-ом состоянии с энергией 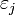, а константа 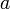определяется условием нормировки:

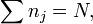
где 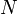— полное число частиц.

Распределение Больцмана является предельным случаем (квантовые эффекты пренебрежимо малы) распределений Ферми — Дирака и Бозе — Эйнштейна, и, соответственно, классический идеальный газ является предельным случаем Ферми-газа и Бозе-газа. Для любого идеального газа справедливо соотношение Майера:

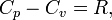
где 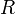— универсальная газовая постоянная, 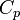— молярная теплоемкость при постоянном давлении, — молярная теплоемкость при постоянном объёме.

1. Тепловое равновесие. Температура как основная характеристика состояния теплового равновесия и направления процесса теплообмена между двумя телами. Абсолютная температура, шкала Кельвина. Измерение температуры.

Термодинамическое равновесие — состояние системы, при котором остаются неизменными по времени макроскопические величины этой системы (температура, давление, объем, энтропия). В общем, эти величины не являются постоянными, они лишь флуктуируют (колеблются) возле своих средних значений.

Температу́ра — скалярная физическая величина, характеризующая приходящуюся на одну степень свободы среднюю кинетическую энергию частиц макроскопической системы, находящейся в состоянии термодинамического равновесия.

1. Дайте понятие идеального газа. Выведите уравнение состояния идеального газа.

Для объяснения свойств вещества в газообразном состоянии используется модель идеального газа. Идеальным принято считать газ, если:

а) между молекулами отсутствуют силы притяжения, т. е. молекулы ведут себя как абсолютно упругие тела;
б) газ очень разряжен, т.е. расстояние между молекулами намного больше размеров самих молекул;
в) тепловое равновесие по всему объему достигается мгновенно. Условия, необходимые для того, чтобы реальный газ обрел свойства идеального, осуществляются при соответствующем разряжении реального газа. Некоторые газы даже при комнатной температуре и атмосферном давлении слабо отличаются от идеальных. Основными параметрами идеального газа являются давление,объем и температура.

На основании использования основных положений молекулярно-кинетической теории было получено основное уравнение МКТ идеального газа, которое выглядит так: 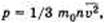, где р—давление идеального газа, m0 — масса молекулы, 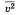среднее значение
концентрация молекул, квадрата скорости молекул.

1. Дайте определение изопроцесса. Сформулируйте газовые законы: закон Бойля- Мариотта, закон Гей-Люссака, закон Шарля.

Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём или температура — остаются неизменными. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический, энтропии — адиабатический. Линии, изображающие данные процессы на какой-либо термодинамической диаграмме, называются изобара, изохора, изотерма и адиабата соответственно. Изопроцессы являются частными случаями политропного процесса.

Дата добавления: 2015-04-24