Собственные электрические колебания в колебательном контуре. Логарифмический декремент затухания и добротность колебания

Колебания электрических величин — заряда, напряжения, тока — можно наблюдать в цепи, состоящей из последовательно соединённых сопротивления (R), ёмкости (C) и катушки индуктивности (L)

Колебания, происходящие только за счёт внутренних энергетических ресурсов системы, называются собственными. Первоначально энергия была сообщена конденсатору и локализована в электростатическом поле. При замыкании конденсатора на катушку, в цепи появляется разрядный ток, а в катушке — магнитное поле. Э.д.с. самоиндукции катушки будет препятствовать мгновенной разрядке конденсатора. Через четверть периода конденсатор полностью разрядится, но ток будет продолжать течь, поддерживаемый электродвижущей силой самоиндукции. К моменту 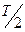эта э.д.с. перезарядит конденсатор. Ток в контуре и магнитное поле уменьшатся до нуля, заряд на обкладках конденсатора достигнет максимального значения.

Эти колебания электрических величин в контуре будут происходить неограниченно долго, если сопротивление контура R = 0. Такой процесс называют собственные незатухающие колебания.

Если сопротивлением резистора R (силой сопротивления в механическом осцилляторе) пренебречь нельзя, то в подобных системах будут происходить собственные затухающие колебания.

Характер затухающих колебаний меняется с увеличением сопротивления резистора R. Когда сопротивление превысит определённое критическое значение R _к, колебания в системе не возникают. Происходит монотонный а периодический разряд конденсатора

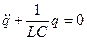. Это линейное дифференциальное уравнение второго порядка — дифференциальное уравнение собственных незатухающих электрических колебаний. Решением этого уравнения является следующая гармоническая функция: q = A cos(w₀ t + j). частота собственных незатухающих колебаний гармонического осциллятора: .

Окончательно закон изменения заряда конденсатора во времени принимает следующий вид:

q = q ₀cos(w₀ t). Ток в цепи при этом меняется так:

Собственные затухающие колебания происходят в колебательном контуре RLC

Эти колебания можно описать следующим дифференциальным уравнением (правило напряжений Кирхгофа): IR – U _C = e^СИ.Здесь по-прежнему: I = 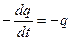; U _C = ; e^СИ = = = .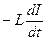

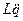Учитывая эти соотношения, уравнению придадим следующий вид:

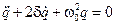; (11.7). есь d = 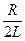— коэффициент затухания; = 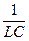— частота собственных незатухающих колебаний. Уравнение 11.7— дифференциальное уравнение собственных затухающих электрических колебаний.

Важной характеристикой затухающего процесса является логарифмический декремент затухания — логарифм отношения амплитуд двух соседних колебаний: . Логарифмический декремент затухания равен произведению коэффициента затухания d на время одного полного колебания (период) Т. Процесс затухания колебания до нуля продолжается бесконечное время, поэтому условно принято считать, что процесс затух, если амплитуда колебаний уменьшилась в е раз.

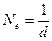и .

Логарифмический декремент затухания d обратен числу колебаний, по истечению которых амплитуда падает в е раз. В радиотехнике для энергетической характеристики затухания часто используют величину, которая получила название добротность контура: .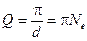

Дата добавления: 2015-04-24