Средняя арифметическая величина

Сущность средней как статистического показателя. Средняя арифметическая, область ее применения.

Средняя величина – это обобщенная количественная характеристика признака в статистической совокупности. Она выражает типичное значение признака для всех единиц совокупности под влиянием всего комплекса факторов. В средней величине погашаются индивидуальные различия единиц совокупности и вариантах усредняемого признака.

Средняя величина является важнейшей категорией статистической науки и важнейшей формой обобщающих показателей. Многие явления и процессы становятся ясными, определенными, лишь будучи обобщенными в форме средних величин. Таковы, например, средняя урожайность, средняя продуктивность животных, средняя производительность труда, средняя себестоимость единицы продукции, средняя заработная плата, средний душевой доход и т.д.

Основным условием правильного применения средних величин является качественная однородность статистической совокупности. Среднее, вычисленные для качественно неоднородной совокупности, теряют свое научное значение. Такие средние являются фиктивными, причем не только не имеющими представление действительности, но искажающими ее и вводящими в заблуждение, так как они стирают существенные различия между явлениями.

Средняя арифметическая простая величина:

,

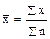где n – число единиц в статистической совокупности.

Средняя арифметическая величина взвешенная величина определяется по формуле:

.

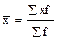где f – локальные частоты (частости).

Расчет средней арифметической простой можно показать на примере ранжированного ряда, составленного по площади посева льна-долгунца в 20 сельскохозяйственных предприятиях района (табл. 6.1.).

Т а б л и ц а. Расчет средней арифметической простой в ранжированном ряду распределения

Ранговые №№	Варианты (значения признака)
Символы	Посевная площадь, га
	Х1
	Х2
	Х3
…	…	…
n	хn
Σ	Σх

Подставив данные табл. в формулу, получаем среднее арифметическое простое значение посевной площади льна-долгунца, приходящиеся на 1 хозяйство:

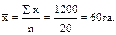
Поскольку в дискретном ряду распределения каждая варианта представлена определенной локальной частотой (частостью), то среднее значение для каждого такого ряда может быть рассчитано по формуле средней арифметической взвешенной, т.е.

,

где х – варианты (значение признака); f – локальные частоты (частости).

Определение средней арифметической взвешенной величины можно показать на примере расчёта средней урожайности льносоломки в 20 сельскохозяйственных предприятиях района, поскольку в этих предприятиях разная посевная площадь (f) (табл.).

Подставив в формулу данные табл., можно рассчитать среднюю арифметическую взвешенную величину для дискретного ряда распределения:

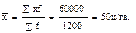
Таким образом, средняя урожайность, взвешенная по посевной площади льна-долгунца, в сельскохозяйственных предприятиях района, составила 50 ц/га льносоломки.

Т а б л и ц а 6.2. Расчет средней арифметической взвешенной в дискретном

Дата добавления: 2015-04-24