Остаточная дисперсия

Факториальная дисперсия

Общая дисперсия

Общая дисперсия вычисляется по формуле:

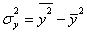
или

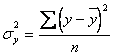
где ;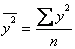

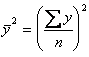
Факториальная дисперсия:

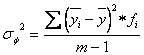
где m - число групп;
f_i - число единиц наблюдения в группе.

Остаточная дисперсия (дисперсия остаточных величин):

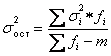
или

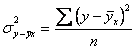
где σ _i ² - групповые дисперсии;
∑f_i - общее число единиц наблюдения;
n - численность выборки.

14. Правила сложения дисперсий.

Выводы о степени взаимосвязи базируются на анализе вариации результативного признака. При этом применяется правило сложения дисперсий:

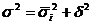
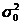- общая дисперсия;

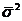- средняя из внутригрупповых дисперсий;

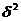- межгрупповая дисперсия.

Общая дисперсия измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию.

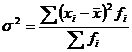
Межгрупповая дисперсия отражает ту часть вариации результативного признака, которая обусловлена воздействием факторного признака. Это воздействие проявляется в отклонении групповых средних от общей средней:

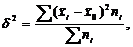
где - среднее значение результативного признака по i-ой группе;

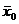- общая средняя по совокупности в целом;

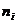- объем (численность) i-ой группы.

Если факторный признак, по которому производится группировка, не оказывает никакого влияния на результативный признак, то групповые средние будут равны между собой и совпадут с общей средней. В этом случае межгрупповая средняя будет равна нулю.

Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и независящую от признака фактора, положенного в основание группировки.

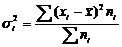
Средняя из внутригрупповых дисперсий отражает ту часть вариации результативного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка:

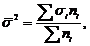
где 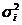- дисперсия результативного признака в i-ой группе;

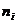- объем (численность) i-ой группы;

Эмпирический коэффициент детерминации представляет собой долю межгрупповой дисперсии в общей дисперсии.

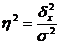
Теснота связи между факторным и результативным признаком оценивается на основе эмпирического корреляционного отношения:

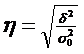
15. Понятие и классификация индексов.

Индекс — это обобщающий относительный показатель, характеризующий изменение уровня общественного явления во времени, по сравнению с программой развития, планом, прогнозом или его соотношение в пространстве.

Наиболее распространена сравнительная характеристика во времени. В этом случае индексы выступают как относительные величины динамики.
Индексный метод является также важнейшим аналитическим средством выявления связей между явлениями. При этом применяются уже не отдельные индексы, а их системы.
В статистической практике индексы применяются при анализе развития всех отраслей экономики, на всех этапах экономической работы. В условиях рыночной экономики особенно возросла роль индексов цен, доходов населения, фондового рынка и территориальных индексов.

Статистика осуществляет классификацию индексов по следующим признакам:

1. В зависимости от объекта исследования:

- индексы объемных (количественных) показателей (индексы физического объема: товарооборота, продукции, потребления)

- индексы качественных показателей (индексы цен, себестоимости, заработной плата)

К индексам объемных показателей относятся индексы физического объема: товарооборота, продукции, потребления материальных благ и услуг; а также других показателей, имеющих количественный характер: численности работников, посевных площадей и т.п. К индексам качественных показателей относятся индексы: цен, себестоимости продукции, заработной платы, производительности труда, урожайности и т.п.;

2. По степени охвата элементов совокупности:

- индивидуальные индексы (дают сравнительную характеристику отдельных элементов явления)

- общие индексы (характеризуют изменение совокупности элементов или всего явления в целом)

3. В зависимости от методологии исчисления общие индексы подразделяются на:

- агрегатные (агрегатные индексы являются основной формой индексов и строятся как агрегаты путем взвешивания индексируемого показателя с помощью неизменной величины другого, взаимосвязанного с ним показателя).

- средние (являются производными от агрегатных)

4. В зависимости от базы сравнения различают:

- базисные (если при исчислении индексов за несколько периодов времени база сравнения остается постоянной)

- цепные (если база сравнения постоянно меняется)

16. Система индексов.

Для построения группового индекса цен нужно учесть структуру продукции, по которой исчисляется индекс. По сравнению с базисным периодом может произойти изменение не только индивидуальных цен изделий, но также и удельных весов отдельных изделий. Для того чтобы исключить искажающее влияние этого фактора, должна быть принята одна и та же структура продукции для базисного периода и на дату исчисления индекса.
Существуют следующие методы исчисления индексе цен: 1) по определённому устойчивому набору продуктов; 2) на основе неизменных удельных весов отдельных групп продукции; 3) на основе удельных весов отдельных групп продукции, складывающихся в том или ином периоде, для которого исчисляется индекс цен; 4) путём прямого пересчёта всей продукции в двух ценах (базисных и действующих).
Индексы цен, исчисляемые на основе постоянного набора продуктов, имеют то, и пожалуй единственное, преимущество, что построение их сравнительно просто, все расчёты их поддаются прямой проверке. Однако показания такого рода индексов могут рассчитывать на достоверность лишь в том случае, если набор продуктов охватывает решающие по количеству и типичные по значению виды продукции. Между тем это по существу исключается самой формой индекса, предполагающей отбор сравнительно ограниченной номенклатуры продуктопредставителей.
Индексы цен, исчисленные на основе неизменных удельных весов продукции, выгодно отличаются от предыдущего типа индексов тем, что они предполагают расчёт изменения цен по всему кругу продукции. Однако соотношения между отдельными группами продукции принимаются неизменными. Поэтому при существенных структурных изменениях в продукции и неодинаковой динамике цен по отдельным группам изделий показания такого индекса не могут быть признаны вполне достоверными.

17. Ряды динамики и их характеристика.

Ряды динамики – статистические данные, отображающие развитие во времени изучаемого явления. Их также называют динамическими рядами, временными рядами.

В каждом ряду динамики имеется два основных элемента:

1. показатель времени t;
2. соответствующие им уровни развития изучаемого явления y;

В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты), либо отдельные периоды (годы, кварталы, месяцы, сутки).

Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами.

Ряды динамики различаются по следующим признакам: 1) По времени. В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим ряды динамики подразделяются на моментные и интервальные.

Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени. Примером моментного ряда динамики является следующая информация о списочной численности работников магазина в 1991 году (таб. 1): Таблица 1[] Списочная численность работников магазина в 1991 году

Дата	0 91	04.91	07.91	10.91	0 92
Число работников, чел.

Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности. Хотя и в моментном ряду есть интервалы – промежутки между соседними в ряду датами, -- величина того или иного конкретного уровня не зависит от продолжительности периода между двумя датами. Так, основная часть персонала магазина, составляющая списочную численность на 0 1991, продолжающая работать в течение данного года, отображена в уровнях последующих периодов. Поэтому при суммировании уровней моментного ряда может возникнуть повторный счет.

Посредством моментных рядов динамики в торговле изучаются товарные запасы, состояние кадров, количество оборудования и других показателей, отображающих состояние изучаемых явлений на отдельные даты (моменты) времени.

Интервальные ряды динамики отражают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени.

Примером интервального ряда могут служить данные о розничном товарообороте магазина в 1987 – 1991 гг. (таб. 2): Таблица 2[] Объем розничного товарооборота магазина в 1987 - 1991 гг.

Год
Объем розничного товарооборота, тыс. р.	885.7	932.6	980.1	1028.7	1088.4

18. Классификация рядов динамики. Измерение уровней рядов динамики.

Ряд динамики — это последовательность упорядоченных во времени количественных статистических величин, характеризующих развитие изучаемого явления или процесса. Конкретное значение величины на­зывается уровнем ряда и обозначается Y, а их число в ряду обозначается n. Ряды динамики классифицируются по следующим признакам.

1. По времени — ряды моментные и интервальные (периодные)
которые показывают уровень явления на конкретный момент времени или на определенный его период. Сумма уровней интервального ряда дает вполне реальную статистическую величину за несколько периодов времени, например, общий выпуск продукции, общее количество проданных акций и т.п. Уровни моментного ряда, хотя и можно суммировать, но эта сумма реального содержания, как правило, не имеет. Так, если сложить величины запасов на начало каж­дого месяца квартала, то полученная сумма не означает квартальную величину запасов.

2. По форме представления — ряды абсолютных, относительных и средних величин.

3. По интервалам времени — ряды равномерные и неравномерные (полные и неполные), первые из которых имеют равные интервалы, а у вторых равенство интервалов не соблюдается.

4. По числу смысловых статистических величин — ряды изолиро­ванные и комплексные (одномерные и многомерные). Первые представ­ляют собой ряд динамики одной статистической величины (например, индекс инфляции), а вторые — нескольких (например, потребление ос­новных продуктов питания).

Дата добавления: 2015-04-24