Средние показатели ряда динамики. Если ряд динамики интервальный и содержит все последовательные уровни, то средний уровень определяется как средняя арифметическая величина: Если ряд динамики

Если ряд динамики интервальный и содержит все последовательные уровни, то средний уровень определяется как средняя арифметическая величина: Если ряд динамики моментный с одинаковыми промежутками времени между датами, то средняя хронологическая определяется как простая арифметическая: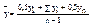

А если с разновеликими интервалами между датами, то как средняя арифметическая взвешенная по времени: 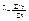где t - время, в течение которого уровень не менялся Средний абсолютный прирост: 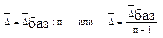Средний темп роста: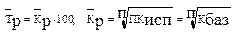

Средний темп прироста: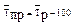

Один из важнейших вопросов, возникающих при изучении рядов динамики - это выявление тенденции развития экономической закономерности в динамике. Для этой цели применяются разнообразные статистические методы, в частности, метод укрупнения интервалов, метод скользящей средней, метод аналитического выравнивания.

Наиболее простым в использовании является метод укрупнения интервалов, основанный на укрупнении периодов времени, к которым относятся уровни ряда. Выявление тенденции осуществляется по новому укрупненному ряду динамики.

Другой метод - метод скользящей средней заключается в замене первоначальных уровней ряда динамики средними арифметическими, найденными по способу скольжения, начиная с первого уровня ряда с постепенным включением последующих уровней.

Наиболее совершенным методом выявления тенденции ряда динамики является метод аналитического выравнивания, который заключается в замене первоначальных уровней ряда новыми, найденными во времени "t" построением аналитического уравнения связи.

Рассмотрим на примере возможности применения каждого из методов выравнивания при выявлении тенденции ряда динамики.

1. По методу укрупнения интервалов имеем новые укрупненные поквартально уровни ряда динамики:

у₁ = 18,6 + 17,3 + 18,9 = 54,8;

y₂ = 18,2 + 17,9 + 19,1 = 55,2 и т.д.

Выровненный ряд динамики примет вид: 54,8 55,2 56,3 57,5.

2. Употребляя те же данные, применим метод скользящей средней, используя семичленную скользящую среднюю. Тогда:

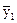= = 18,5;

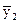= = 18,4 и т.д.

Выравненный с помощью семичленной скользящей средней ряд динамики примет вид: 18,5 18,4 18,6 18,7 18,8 19,0.

3. Используя метод отсчета от условного нуля введем условное обозначение времени "t", придав ему определенные значения так, чтобы?t = 0 (см. табл. 6.2).

Судя по выявленной с помощью двух предыдущих методов тенденции выпуска молдингов в течение года, можно сказать, что наиболее вероятна линейная зависимость данного распределения от времени "t" и данному распределению соответствует уравнение прямой 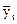= a₀ + a₁t.

Для нахождения параметров a₀ и a₁ используем систему уравнений

,

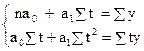так как?t = 0, о имеем

a₀ = 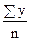= = 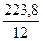18,6;

a₁ = 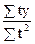= = 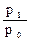0,09.

27. ОШИБКИ ВЫБОРОЧНОГО НАБЛЮДЕНИЯ. ОПРЕДЕЛЕНИЕ НЕОБХОДИМОЙ ЧИСЛЕННОСТИ ВЫБОРКИ.

Выборочное - наблюдение, при котором характе­ристика всей совокупности фактов дается по некоторой их части, отобранной в случайном порядке.

Подлежащая изучению статистическая сово­купность, из которой производится отбор части единиц, называется генеральной совокупностью. Отобранная из гене­ральной совокупности некоторая часть единиц, подвергаю­щаяся обследованию, называется выборочной совокупностью, или просто выборкой.

В генеральной совокупности доля единиц, обладающих изучаемым признаком, называется генеральной долей (обозна­чается р), а средняя величина изучаемого варьирующего при­знака - генеральной средней (обозначается х с чертой сверху).

В выборочной совокупности долю изучаемого признака называют выборочной долей, или частостью (обозначается w), а среднюю величину в выборке - выборочной средней (обозна­чается х с волнистой чертой - х ~ ).

Поскольку изучаемая статистическая совокупность сост. из ед-ц с варьирующими признаками, то состав выборочной совокупности может в той или иной степени отличаться от состава генеральной совокупности. Это значит, что обобщающие показатели в выборке (w и х~) могут в той или иной мере отличаться от значений этих характеристик в генеральной совокупности (р и ‾х).

N – число ед-ц в генеральной сов-ти, n- число ед-ц в выборке.

Возможные расхождения между характеристиками выбо­рочной и генеральной совокупностей измеряются средней ошибкой выборки µ.

Предельная ошибка выборки – Δ.

Δ = µ * t, где t – коэффициент доверия. Опр-ся по таблице..Теоретической основой выборочного метода явл-ся теоремы Чебушева и Ляпунова.

Теорема Чебушева.

С вер-тью, близкой к 1, можно утверждать, что при достаточно большом числе наблюдений выборочные характеристики будут сколь угодно мало отличаться от генеральных хар-к.

Величина ошибки может быть записана в след виде:

Д х = | х ~ - х ‾ | = tµ - для количественного признака

Д w = |w – p| = t µ - для альтернативного признака

Д х = (+-t корень((сигма по х) квадрат) / n * (1-n/N))

Д w = +- t корень (w(1-w)/n*(1-n/N))

х ~ - Д х <или= х ‾ <или = х ~ + Д х

w - Д w <или= p <или= w + Д w

Размер ошибки выборки зависит от численности выборочной совокупности. Поэтому вопрос об оптимальной численности выборки имеет важное значение. Расчет оптимальной численности выборки таков:

Д = +- t корень((G^2 / n) * (1 – n/N))

+- корень((G^2 / n) * (1 – n/N)) = Д/t

(G^2 / n) * (1 – n/N) = (Д/t) ^2

G^2 * (1 – n/N) = (Д/t)^2 * n

G^2 – ((G^2 * n) / N) = (Д/t) ^2 * n

(G^2 / n) – (G^2 / N) = (Д/t) ^2

(G^2 / n) = (Д/t) ^2 + (G^2 / N)

n = G^2 / ((Д/t) ^2 + (G^2 / N))

n = G^2 / ((Д ^2 * N) + (G * t) ^2) / N * t ^2)

n = (G^2 * N * t ^2) / Д ^2 * N + (G* t) ^2

обозначения:

G – сигмаG^2 – сигма в квадратеХ^2 - что-то в квадрате

Д – это дельта, ошибка (треугольник).

Дата добавления: 2015-04-24