Область практического применения относительных величин в изучении экономических явлений

15. Понятие средних величин, их виды и условия применения. Средние величины имеют большое значение в статистике коммерческой деятельности. В них отображаются важнейшие показатели товарооборота, тов-х запасов, цен. Средними величинами характ-ся качеств. показатели коммерч. Деят-ти (прибыль, рентабельность). Ср.величины – это обобщ-е показатели выражающие характ-е, типичные, свойств-е больш-ву призн-в размеры и соотношения. Осн-я важность ср. показателей, то, что они опред-т законом-ти разв-я изучаемого явления. Ср-й уров. Прзнака = .

В стат. исп-т разл-е виды ср. величин: - средн. арифметич. (сам. Распростр.); - средн. гармонич-я; - средн. геометрич-я; - средн. квадратич-я; - средн. хронологич-я.

В социально-экономическом анализе используются два класса средних величин:- степенные средние;- структурные средние. К степенным средним относятся несколько видов средних, построенных по одному общему принципу:

Показатель степени k может принимать любые значения, но на практике обычно используются несколько его значений: при k = 1 получают среднюю арифметическую; k = -1 – среднюю гармоническую; k = 0 –среднюю геометрическую; k =2 – среднюю квадратическую. Степенные средние в зависимости от формы представления исходных данных могут быть простыми и взвешенными. Если исходные данные представлены простым перечислением значений признака у статистических единиц, то используется формуластепенной средней простой:

Если данные предварительно сгруппированы (представлены рядом распределения), то используется формула степенной средней взвешенной:

16. Методика расчёта средней арифметической (простой и взвешенной). Средняя арифметическая является наиболее распространенным видом степенных средних, используется в случаях, когда объём усредняемого признака является аддитивной величиной, т.е. образуется как сумма его значений по всем единицам статистической совокупности. Средняя арифметич. быв-т: простая и взвешенная. Простая: , -индивид. знач-е признака; n-колич-во ед. совок-ти. Она применяется в тех случ-х, когда каждое индивид-е знач-е признака встреч-ся 1 раз или одинак. колич. раз. Средняя арифметическая простая используется при работе с несгруппированными данными.

Если в исходных данных отдельные значения усредняемого признака повторятся, то расчет средней проводится по сгруппированным данным иливариационным рядам. В подобных случаях для расчета необходимо применять среднюю арифметическую взвешенную – среднююсгруппированных величин. Взвешенная: если варианты или знач. признака встреч-ся не одинак. колич. раз, то исп-ся средняя арифметич. взвешенная. , Х- варианты значен. признака; f – частота появл. соотв-го значен. признака.

17. Методика расчёта средней арифметической взвешенной в дискретном и интервальном рядах распределения. Ряды распределения довольно часто встречаются в статистической практике. При этом варианта может быть задана в виде интервалов, если признак непрерывный, или в виде индивидуальных значений, если ряд дискретный. Для дискретных рядов расчет осуществляется по вышеприведенной формуле средней арифметической взвешенной. Для интервального ряда распределения задача расчета средней величины решается следующим образом. Предполагаем, что в пределах интервала значения признаков располагаются равномерно, поэтому середина интервала будет величиной, характеризующей весь интервал, то есть наиболее типичным для него значением. Данное предположение не всегда выполняется поэтому, чем меньше величина интервала, тем точнее его середина будет характеризовать весь интервал. Далее используется обычная формула средней, только значения варианты будут приравниваться к середине соответствующего интервала. Расчет средней по непрерывному признаку (представленному в виде интервалов) был рассмотрен в примере 2.

В том случае, если ряд распределения имеет равные интервалы, расчет средней может быть существенно упрощен. Упрощенные способы расчета средней арифметической базируются на знании ее свойств.

Свойства средней арифметической:

• если все веса (f) увеличить или уменьшить в одинаковое число раз (d), то величина средней не изменится:

• если каждую варианту (х) увеличить или уменьшить на одну и ту же величину, то средняя увеличится или уменьшится на эту же величину:

• если каждую варианту (х) увеличить или уменьшить в одно и то же число раз (h), то средняя увеличится или уменьшится в то же число раз.

• сумма отклонений вариант от средней, взвешенных их частотами равна нулю:

Перечисленные свойства средней арифметической используются при расчете средней способом моментов или способом отсчета от условного начала (0). При использовании этого способа последовательно осуществляются следующие операции:

• определяются срединные значения интервалов как полусумма начала и конца интервалов;
• варианта (серединное значение интервала) с наибольшей частотой принимается за условное начало отсчета (А);
• рассчитывается момент 1-го порядка:

где

i	— величина интервала.

Средняя рассчитывается по формуле:

18. Методика расчёта средней гармонической и область её практического применения. Средняя гармоническаяимеет более сложную конструкцию, чем средняя арифметическая. Используется в тех случаях, когда статистическая информация не содержит частот по отдельным значениям признака, а представлена произведением значения признака на частоту. Когда известен ряд вариант (Х), ряд произвед-й (Хf), f – неизв-но, в этом случае средняя рассчитыв-ся по ф-ле сред. гармонич. взвеш-й: 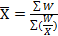, W=Xf В зависимости от формы представления исходных данных средняя гармоническая может быть рассчитана как простая и как взвешенная. Если исходные данные несгруппированны, то применяется средняя гармоническая простая:

К ней прибегают в случаях определения, например, средних затрат труда, материалов и т. д. на единицу продукции по нескольким предприятиям.

При работе со сгруппированными данными используется средняя гармоническая взвешенная:

19. Средняя геометрическая: методика расчёта и область практического применения. Средняя геометрическая. Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака (например, между 100 и 1000000). Существуют формулы для простой и взвешенной средней геометрической. Для простой средней геометрической

Для взвешенной средней геометрической

20. Методика расчёта моды и медианы и область их практического применения. Медиана (Ме) - это величина, которая соответствует варианту, находящемуся в середине ранжированного ряда.Для ранжированного ряда с нечетным числом индивидуальных величин (например, 1, 2, 3, 3, 6, 7, 9, 9, 10) медианой будет величина, которая расположена в центре ряда, т.е. пятая величина.Для ранжированного ряда с четным числом индивидуальных величин (например, 1, 5, 7, 10, 11, 14) медианой будет средняя арифметическая величина, которая рассчитывается из двух смежных величин. Для нашего случая медиана равна (7+10): 2= 8,5. То есть для нахождения медианы сначала необходимо определить ее порядковый номер (ее положение в ранжированном ряду) по формуле

где n - число единиц в совокупности. Численное значение медианы определяют по накопленным частотам в дискретном вариационном ряду. Для этого сначала следует указать интервал нахождения медианы в интервальном ряду распределения. Медианным называют первый интервал, где сумма накопленных частот превышает половину наблюдений от общего числа всех наблюдений. Численное значение медианы обычно определяют по формуле

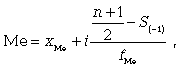
где x_Ме - нижняя граница медианного интервала; i - величина интервала; S_-1 - накопленная частота интервала, которая предшествует медианному; f - частота медианного интервала. Модой (Мо) называют значение признака, которое встречается наиболее часто у единиц совокупности. Для дискретного ряда модой будет являться вариант с наибольшей частотой. Для определения моды интервального ряда сначала определяют модальный интервал (интервал, имеющий наибольшую частоту). Затем в пределах этого интервала находят то значение признака, которое может являться модой.Чтобы найти конкретное значение моды, необходимо использовать формулу

где x_Мо - нижняя граница модального интервала; i_Мо - величина модального интервала; f_Мо - частота модального интервала; f_Мо-1 - частота интервала, предшествующего модальному; f_Мо+1 - частота интервала, следующего за модальным.Мода имеет широкое распространение в маркетинговой деятельности при изучении покупательского спроса, особенно при определении пользующихся наибольшим спросом размеров одежды и обуви, при регулировании ценовой политики

21. Статистические показатели вариации признаков и их экономический смысл.Для измерения вариации признака используют как абсолютные, так и относительные показатели.К абсолютным показателям вариации относят: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсию.К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение и др. Размах вариации R. Это самый доступный по простоте расчета абсолютный показатель, который определяется как разность между самым большим и самым малым значениями признака у единиц данной совокупности:

Размах вариации (размах колебаний) - важный показатель колеблемости признака, но он дает возможность увидеть только крайние отклонения, что ограничивает область его применения. Для более точной характеристики вариации признака на основе учета его колеблемости используются другие показатели. Среднее линейное отклонение d, которое вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности. Эта величина определяется как средняя арифметическая из абсолютных значений отклонений от средней. Так как сумма отклонений значений признака от средней величины равна нулю, то все отклонения берутся по модулю.Формула среднего линейного отклонения (простая)

Формула среднего линейного отклонения (взвешенная)

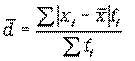При использовании показателя среднего линейного отклонения возникают определенные неудобства, связанные с тем, что приходится иметь дело не только с положительными, но и с отрицательными величинами, что побудило искать другие способы оценки вариации, чтобы иметь дело только с положительными величинами. Таким способом стало возведение всех отклонений во вторую степень. Обобщающие показатели, найденные с использованием вторых степеней отклонений, получили очень широкое распространение. К таким показателям относятся среднее квадратическое отклонение 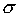и среднее квадратическое отклонение в квадрате , которое называют дисперсией. Средняя квадратическая простая

Средняя квадратическая взвешенная

Дисперсия есть не что иное, как средний квадрат отклонений индивидуальных значений признака от его средней величины.

Формулы дисперсии взвешенной и простой :

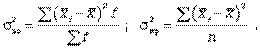(6.6)

Расчет дисперсии можно упростить. Для этого используется способ отсчета от условного нуля (способ моментов), если имеют место равные интервалы в вариационном ряду.

Кроме показателей вариации, выраженных в абсолютных величинах, в статистическом исследовании используются показатели вариации (V), выраженные в относительных величинах, особенно для целей сравнения колеблемости различных признаков одной и той же совокупности или для сравнения колеблемости одного и того же признака в нескольких совокупностях.

Данные показатели рассчитываются как отношение размаха вариации к средней величине признака (коэффициент осцилляции), отношение среднего линейного отклонения к средней величине признака (линейный коэффициент вариации), отношение среднего квадратического отклонения к средней величине признака (коэффициент вариации) и, как правило, выражаются в процентах.

Формулы расчета относительных показателей вариации:

где V_R - коэффициент осцилляции; - линейный коэффициент вариации; - коэффициент вариации.

Из приведенных формул видно, что чем больше коэффициент V приближен к нулю, тем меньше вариация значений признака.

В статистической практике наиболее часто применяется коэффициент вариации. Он используется не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).

22. Правило сложения дисперсии.Различают три вида дисперсий:общая; средняя внутригрупповая; межгрупповая. Общая дисперсия (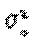) характеризует вариацию признака всей совокупности под влиянием всех тех факторов, которые обусловили данную вариацию. Эта величина определяется по формуле

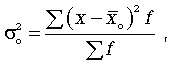(6.8)где - общая средняя арифметическая всей исследуемой совокупности. Средняя внутригрупповая дисперсия () свидетельствует о случайной вариации, которая может возникнуть под влиянием каких-либо неучтенных факторов и которая не зависит от признака-фактора, положенного в основу группировки. Данная дисперсия рассчитывается следующим образом: сначала рассчитываются дисперсии по отдельным группам (), затем рассчитывается средняя внутригрупповая дисперсия :

где n_i - число единиц в группе. Межгрупповая дисперсия (дисперсия групповых средних) характеризует систематическую вариацию, т.е. различия в величине исследуемого признака, возникающие под влиянием признака-фактора, который положен в основу группировки. Эта дисперсия рассчитывается по формуле

где - 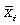средняя величина по отдельной группе.Все три вида дисперсии связаны между собой: общая дисперсия равна сумме средней внутригрупповой дисперсии и межгрупповой дисперсии:

(6.11)Данное соотношение отражает закон, который называют правилом сложения дисперсий. Согласно этому закону (правилу), общая дисперсия, которая возникает под влиянием всех факторов, равна сумме дисперсий, которые появляются как под влиянием признака-фактора, положенного в основу группировки, так и под влиянием других факторов. Благодаря правилу сложения дисперсий можно определить, какая часть общей дисперсии находится под влиянием признака-фактора, положенного в основу группировки.

Дата добавления: 2015-04-24