Характеристика статистического распределения. Мода. Медиана.

Графический метод в статистике. Элементы и классификация статистических графиков.

Расчет средних величин и показателей вариации методом условных (центральных) моментов.

Способ моментов

Часто мы сталкиваемся с расчетом средней арифметической упрощенным способом. В этом случае используются свойства средней величины. Метод упрощенного расчета называется методом условных (центральных) моментов, либо способом отсчета от условного нуля.

Способ моментов предполагает следующие действия:

1) Если возможно, то уменьшаются веса.

2) Выбирается начало отсчета – условный нуль. Обычно выбирается с таким расчетом, чтобы выбранное значение признака было как можно ближе к середине распределения. Если распределение по своей форме близко к нормальному, но за начало отсчета выбирают признак, обладающий наибольшим весом.

3) Находятся отклонения вариантов от условного нуля.

4) Если эти отклонения содержат общий множитель, то рассчитанные отклонения делятся на этот множитель.

	Пример:

до 70			-30	-3	-45
70-80			-20	-2	-34
80-90			-10	-1	-13
90-100
100-110
110-120
120-130
130-140
140 и более
Сумма					-12

Сущность графического метода составляет наглядное представление наличия и направления взаимосвязей между признаками. Для этого значение факторного признака X располагается по оси абсцисс, а значение результативного признака по оси ординат. По совместному расположению точек на графике делают вывод о направлении и наличии зависимости.

Если точки на графике расположены беспорядочно (а), то зависимость между изучаемыми признаками отсутствует.

Если точки на графике концентрируются вокруг прямой (б)/, зависимость между признаками прямая.

Если точки концентрируются вокруг прямой (в)\, то это свидетельствует о наличии обратной зависимости.

Существует множество видов графических изображений. Их классификация основана на ряде признаков, в основе которых;

• способ построения графического образа;

• геометрические знаки, изображающие статистические показа­тели;

• задачи, решаемые с помощью графического изображения.

Классификация статистических графиков по форме графического образа:

• Линейные (стат.кривые);

• Плоскостные (квадратные, секторные, точечные, фоновые и т.д.);

• Объемные (поверхностного распределения).

По способу построения статистические графики делятся на диаг­раммы и статистические карты.

А так же возможно построение Гистограммы(ось Х-интервалы, ось У - частости), Кумуляты (ось Х – накопленные частоты) и Огивы (где оси Х и У поменяны местами)

Стат ряд распр-я – упорядоченное распределение единиц совокупности на группы по определённому группировочному признаку.

2 вида: 1.Атрибутивные ряды – образованы по качественному признаку 2. Вариационные ряды – образованы по количественному признаку.(дискретные и интервальные вар.ряды – состоят из двух элементов: варианты и частоты)

Структурные средние величины.

Мода - это величина признака (варианта), наиболее часто повторяющаяся в изучаемой совокупности. Для дискретных рядов распределения модой будет значение варианта с наибольшей частотой.

где - начальное значение интервала, содержащего моду;

- величина модального интервала;

- частота модального интервала;

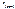- частота интервала, предшествующего модальному;

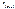- частота интервала, следующего за модальным.

Медиана - это варианта, расположенная в середине вариационного ряда. Если ряд распределения дискретный и имеет нечетное число членов, то медианой будет варианта, находящаяся в середине упорядоченного ряда.

в числителе должна быть ∑f

где — начальное значение интервала, содержащего медиану;

— величина медианного интервала;

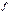— сумма частот ряда;

— сумма накопленных частот, предшествующих медианному интервалу;

— частота медианного интервала.

Дата добавления: 2015-04-24