Средняя величина как обобщающая характеристика совокупности. Научные принципы расчета средних величин

Правила построения статистических таблиц.

См. выше.

Виды статистических группировок.

Результаты сводки и группировки материалов статистического наблюдения представляются, как правило, в виде статистических таблиц, которые должны содержать сводную качественную характеристику изучаемой совокупности по одному или нескольким существенным признакам.

Каждая таблица состоит из подлежащего и сказуемого. Подлежащее – то, о чем говорится в таблице (объект изучения); сказуемое – то, что говорится о подлежащем, его характеристика с помощью системы показателей. Подлежащее обычно располагается в левой части таблицы, сказуемое – в верхней в виде названия граф.

Таблицы бывают:

· Простые (перечневые, когда подлежащее – перечень единиц, составляющих объект изучения);

· Территориальные (дается перечень территорий, стран, областей. Городов);

· Хронологические (в подлежащем – даты)

· Сложные (групповые или комбинированные).

Практикой выработаны определенные требования к составлению и оформлению таблиц:

· Статистическая таблица обязательно имеет заголовок, в котором должны быть указаны цель построения таблицы, территория и время, к которым относятся данные);

· Таблица по возможности должна быть краткой;

· В таблице желательно давать нумерацию граф.

· Приводимые в подлежащем и сказуемом признаки должны быть в логическом порядке с учетом необходимости рассматривать их совместно.

· Таблица может сопровождаться примечаниями, в которых указываются источники данных, более подробно раскрывается содержание показателей.

· Округленные числа в таблицах приводятся с одинаковой степенью точности.

11. Абсолютные величины: их виды и особенности.

Статистика изучает количественную сторону мас­совых явлений и процессов с помощью статистиче­ских величин, которые делятся на абсолютные и от­носительные величины.

Абсолютные величины характеризуют размеры в конкретных условиях времени и места. Они дают ха­рактеристику всей совокупности.

Единицы измерения абсолютных величин;

1) натуральные, отражающие природные свойства явления, — физическая мера веса, длины и др. Ос­новной недостаток натуральных единиц измерения заключается в том, что невозможно суммирование различных натуральных абсолютных величин;

2) условно-натуральные (используются с целью суммирования разной по форме продукции потре­бительского назначения);

3) комбинированные. Их получают в результате пе­ремножения или деления двух натуральных единиц измерения;

4) стоимостные (денежные). Устраняют недостат­ки предыдущих единиц измерения, позволяю оценить разнородную продукцию.

Однако абсолютные величины не дают всеобъем­лющей характеристики исследуемых явлений и про­цессов и не всегда пригодны для сравнения. Это вы­зывает необходимость использования относительных величин, которые используются при сопоставлениях, сравнениях и исполняют роль меры соотношения.

Относительные величины — это отвлеченные статистические величины, выражающие количествен­ное соотношение двух величин.

12. Относительные величины: формы выражения, виды и особенности применения в экономическом анализе.

ü Виды относительных величин:

1) относительные величины динамики — это от­ношение фактической величины показателя в от­четном периоде (у₁) к фактической его величине в базисном, предшествующем периоде (у₀):

ОВД = Y₁/Y₀ х 100%.

Относительные величины динамики характери­зуют изменение явления во времени. В статисти­ке эти показатели называются темпами роста;

2) относительные величины выполнения плана — это отношение фактической величины показателя (у₁) к плановой его величине (у_плана) того же периода:

ОВВП= У₁ /У_плана х 100%.

Эта относительная величина показывает степень выполнения плана в процентах;

3) относительная величина выполнения планового задания — это отношение планируемой величины показателя (у_плана) к фактически достигнутой величине в предшествующем периоде, т.е. в базисном (у₀):

ОВПЗ = У_ллана/У₀ х 100%.

Показывает, на сколько процентов плановое зада­ние выше (ниже) фактически достигнутого в базис­ном периоде. Эту величину называют плановым темпом роста;

4) относительная величина структуры показы­вает состав явления, выраженный в форме доли или удельного веса. Доля (d) — это отношение ча­сти к целому, т.е. отношение составных частей со­вокупности к ее общему объему. Удельный вес — это доля, выраженная в процентах. Относительные величины структуры используются в статистике для характеристики структурных сдвигов;

5) относительная величина координации — пока­зывает соотношение частей целого, т.е. отноше­ние последовательно всех частей к одной из них, взятой за базу. За базу принимают наименьшее значение. Относительная величина координации показывает, сколько единиц данной части целого приходится на другую ее часть, принятую за базу сравнения;

6) относительная величина интенсивности — это отношение двух разноименных величин, связанных между собой. Характеризует степень развития ка­кого-либо явления в определенной среде;

7) относительная величина сравнения — это отно­шение одноименных величин, характеризующих разные объекты изучения за один и тот же период. Показывает, во сколько раз числитель больше (меньше) знаменателя.

Метод средних величин является одним из наибо­лее важных методов в статистике, потому что средние величины широко используются в анализе, на практи­ке, при установлении закономерностей тенденций, связей и для множества других целей. Суть средних величин состоит в том, что они одним числом характе­ризуют уровень исследуемого признака. Отличитель­ной особенностью средних величин является то, что они представляют собой обобщающие показатели.

Средняя величина — это обобщающий показа­тель, выражающий типичный уровень (размер) варьи­рующего признака в расчете на единицу совокупно­сти (качественно однородной).

Средняя величина отражает то общее, что скры­вается в каждой единице совокупности. Она улавли­вает общие черты, общие закономерности, которые проявляются в силу закона больших чисел. Говоря о средних величинах, имеют в виду, что они характе­ризуют всю совокупность в целом, однако, наряду со средней необходимо приводить данные об отдельных единицах совокупности.

Задачи, решаемые с помощью метода средних величин:

1) характеристика уровня развития исследуемого яв­ления;

2) сравнение двух или нескольких уровней иссле­дуемых совокупностей;

3) характеристика изменения уровня явления во вре­мени;

4) выявление и характеристика связей между иссле­дуемыми совокупностями.

Принципы построения средних величин:

1) средние величины могут быть рассчитаны только лишь для качественно однородных совокупностей;

2) средние величины не должны быть абстрактными, т.е. только количественными показателями. Они должны давать качественно-количественную ха­рактеристику исследуемому явлению. Поэтому в статистике средняя величина представляет со­бой не абстрактное, отвлеченное число, а вполне конкретный показатель, относимый к какому-либо явлению, месту, времени;

3) выбор единицы совокупности, по отношению к ко­торой рассчитывается средняя величина, должен быть теоретически обоснован.

Выделяются следующие основные виды средних вели­чин: средняя арифметическая; средняя гармоническая; средняя квадратическая; средняя геометрическая.

Перечисленные средние (кроме средней геометрической) объединяются в общей формуле средней степенной (при различной величине k):

где х - средняя величина исследуемого явления;

х_i – i -й вариант осредняемого признака (i = 1, n);

f_i - вес i -гo варианта.

Помимо степенных средних в статистической практике также ис­пользуются средние структурные, среди которых наиболее распрост­ранены мода и медиана.

14. Средняя арифметическая: простая и взвешенная.

Основной средней величиной является средняя арифметическая. Выделяют простую и взвешен­ную среднюю арифметическую.

Базой для расчета простой средней арифметиче­ской являются первичные записи результатов наблю­дения. Предположим, что известны значения призна­ка х₁, х₂.....х_т. Каждое из этих значений повторяется один раз (или теоретически одинаковое количество раз), т.е. данные не сгруппированы. Тогда для такого ряда следует использовать формулу средней ариф­метической простого ряда или простую среднюю арифметическую:

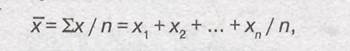
где х — значение варьирующегося признака; п — число единиц совокупности. Базой для расчета взвешенной средней арифмети­ческой является обработанный цифровой материал, т.е. сгруппированные данные. Для таких данных использу­ется формула средней арифметической взвешенной:

где х — значение варьирующегося признака;

т — веса, т.е. частоты, показывающие, сколько раз повторяется каждое значение признака в дан­ной совокупности. Формула получена путем взве­шивания значений каждой варианты и деления суммы вариант на сумму весов. Формулы простой и взвешенной средней арифме­тической не эквивалентны друг другу.

Свойства средней арифметической:

1) алгебраическая сумма отклонений всех вариантов от средней арифметической равна нулю:

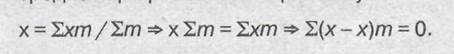
Это свойство используется для проверки правиль­ности расчетов;

2) сумма квадратов отклонений вариант от их сред­ней арифметической больше суммы квадратов отклонений вариант от любого другого числа, не рав­ного средней арифметической:

3) среднее алгебраическое суммы нескольких варьи­рующихся признаков равно сумме средних этих признаков:

Это свойство позволяет определить сумму путем суммирования значений каких-либо признаков;

4) если все варианты (х) увеличить или уменьшить на какое-либо постоянное число (а), средняя (х) уве­личится или уменьшится на то же самое число (у):

5) если все варианты (х) увеличитьили уменьшить в од­но и то же число раз (в), то средняя арифметическая увеличится или уменьшится вто же самое число раз:

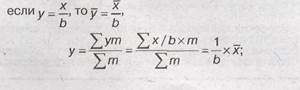
15. Средняя гармоническая: простая и взвешенная.

При решении задач расчет средней величины на­чинается с составления исходного отношения — ло­гической словесной формулы средней. Она состав­ляется на основе теоретического и логического анализа. Иногда среднюю арифметическую нельзя использовать. В этом случае в зависимости от ситуа­ции применяется одна из трех форм средней – средняя гармоническая, средняя квадратическая или средняя геометричекая.

Средняя гармоническая простая строится по формуле:

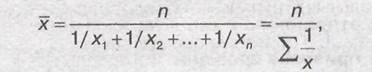
где n —число единиц совокупности или число вариантов; х —значения варьирующегося признака.

Средняя гармоническая простая используется для несгруппированных данных.

Средняя гармоническая взвешенная строится по формуле:

Где х – значения варьирующего признака; m – веса; n – число единиц совокупности.

Дата добавления: 2015-04-24