Фрактальный анализ эволюции КЭМП

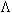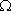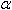Состояние человека характеризуется локальной КЭМП ( i,j) и глобальной КЭМП. (Bi,jk = i i,jk 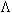jk). Кроме того, существует взаимодействие человека с человеком, характеризуемое матрицей Р. Все эти характеристики изменяются в пространствевремени. Мы рассмотрим изменение во времени. Пусть КОСМОЭНЕРГЕТ активизировал энергетику человека. Другими словами активизировал локальную КЭМП, например элемент 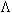i,j. Будем считать, что состояние полной активизации (полной гармонизации) соответствует условно 1. А состояние полного закрытия чакра соответствует 0. То есть Где - нормировочная (эталонная) локальная КЭМП. После активизации возможны различные сценарии изменения . Мы рассмотрим случай, когда после активизации идет процесс релаксации к загрязненному состоянию. Обычно, для исследования процесса релаксации используется уравнение типа

(11)

с начальным условием . В (11) t0 - характерное время релаксации процесса. Уравнение (11) дает экспоненциальный закон эволюции матрицы. Попытки получения других и, особенно степенных законов релаксации при традиционном подходе сталкиваются с трудностями принципиального характера и возникает необходимость перехода к нелинейным уравнениям, для которых, как известно, не существует общего решения. В настоящее время при рассмотрении сложных процессов используется математический аппарат интегродифференцирования дробного порядка. Вместо уравнения (11) используем уравнение в дробных производных [7]

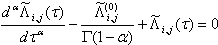(12)

где 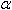- параметр фрактальности процесса, и изменяется в пределах n-1, n,n=1,2,3,... - безразмерное время. Рассмотрим случай с n=1, (0 1). Тогда решение уравнения (12) принимает вид
(13)
при 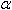выражение 13 принимает вид . Во всех остальных случаях мы имеем не экспоненциальный характер релаксации (например по степенному) закону, когда система практически выходит на постоянное значение, не превращаясь в нуль за характерные времена рассматриваемого процесса.
Принципиальное отличие (12) от (11) в том, что фактически (12) представляет из себя бесконечное множество дифференциальных уравнений. Более того мы явно имеем и соответствующее бесконечное множество решений (13). Наличие бесконечного множества решений (13) позволяет рассмотреть вопрос о разложении экспериментально наблюдаемой функции по базису функций фрактального уравнения. В результате такого разложения фрактальная размерность 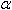становится функцией состояния. Полученная функция состояния 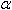= 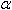(t) позволяет определить динамическое состояние системы с точки зрения взаимодействия как с самим собой так и с окружающей средой. Другими словами, полученная зависимость позволяет одновременно анализировать влияние различных уровней системы на заданный процесс. Тем самым удается одновременно анализировать взаимодействие нескольких уровней организации реальности. В результате такого анализа удается из экспериментально наблюдаемых данных восстановить природу тех процессов которые и формируют наблюдаемые параметры. Например, если мы имеем зависимость от времени давления крови на каком либо участке тела (экспериментально измеренная функция Pэксп(t)). То вычисляя 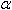= 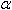(t) из уравнения Pэксп(t)=P0Ea,1(-t/t0)a) мы увидим, во первых полученная зависимость 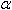= 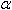(t) у больного и здорового человека отличаются, и, причем характерное время t0 природа которого и содержит параметры рассматриваемого процесса и объекта, также окажутся разными. Вот именно эта разница и может служит основой классификации воздействия на человека внешних воздействий в том числе и космических частот. Примеры такого анализа различных экспериментальных данных и более подробное изложение рассматриваемого фрактального анализа можно найти в работах [8,9].
Для анализа динамики воздействия космических частот на человека необходимо снять данные в цифровом формате с какого либо органа или участка тела человека, например с печени, или различные ритмы головного мозга, до и после воздействия определенной космической частоты. По изложенному выше фрактальному анализу определить функции 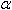= 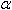(t) и характерное время t0. Характерное время t0 - важнейшая характеристика системы. Например когда речь идет о процессах диффузии то где l - характерный масштаб среды, D - коэффициент диффузии, параметр среды. Определяя t0 из фрактального анализа и зная l можно определить D. Это осуществлено, например в [9]. Когда речь идет о релаксации между различными состояниями энергетического центра необходимо также определить природу времени релаксации t0 энергетического состояния человека. Природа t0 так или иначе определяется отношением X (некоторое характерное время). В качестве негативного имеется ввиду все то что блокирует энергетический центр (например зависть) под положительным понимается то, что открывает центр для взаимодействия с космической частотой (например пожелания добра). Что же касается «некоторого характерного времени», то в качестве него можно взять определенные циклы и ритмы организма. Природа t0 - сложный вопрос, который уточняется при рассмотрение конкретного эксперимента взаимодействии космической частоты с человеком.

Дата добавления: 2015-05-07