Проводиться за критерієм Фішера

.

Але тоді природно і рішення одержати в матричному записі, у виді зворотної матриці:

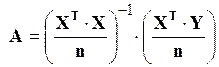
Зауваження:

Якщо будувати рівняння регресії у виді багаточлена

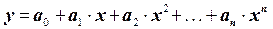
і при цьому використовувати матричний спосіб складання і рішення нормальної системи, то формули анітрошки не зміняться, тільки матриця Х вихідних даних буде містити вже n стовпців.

Перевірка адекватності квадратичного рівняння регресії

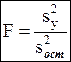
Проводиться порівняння двох дисперсій: виправленої дисперсії фактора Y і дисперсії залишків

· виправлена дисперсію Y: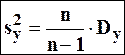

· дисперсія залишків: .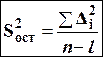

-число коефіцієнтів у рівнянні регресії, тобто вираз 3.

Підраховане значення критерію, що спостерігається, порівнюємо зі знайденим з таблиць критичним значенням Фішера. Для користування таблицями задаємо рівень значимості і числа ступенів свободи:

Чим більше F _р у порівнянні з F _кр, тим вище адекватність. Порівнюючи, робимо висновок про адекватність (або неадекватності) побудованої кореляційної моделі причому оцінюємо і ступінь адекватності.

Багатофакторна лінійна економетрична модель

Рівняння багатофакторної (множинної) лінійної регресії має вигляд:

.

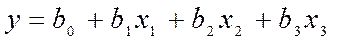Методом найменших квадратів (1МНК) обчислюються оцінки невідомих параметрів модел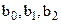і і 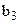у наступній послідовності формування матриць коефіцієнтів і правих частин:

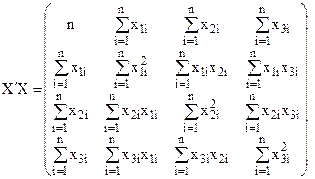
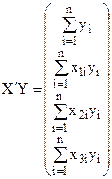
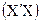Далі знаходиться матриця , обернена до матриці ; і обчислюється вектор оцінок параметрів моделі за допомогою добутку матриць:

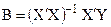, перший елемент якого значення параметра b₀, далі b₁, b₂, b₃.

Множинна кореляція

Використовуючи Пакет аналізу в MS Excel:

– Сервис → Анализ данных → Регрессия - знаходиться множинна кореляції R;

– Сервис → Анализ данных → Корреляция - знаходиться кореляційна матриця.

Множинний коефіцієнт детермінації

Використовуючи Пакет аналізу в MS Excel:

– Сервис → Анализ данных → Регрессия - знаходиться R квадрат;

Способи отримання параметрів рівняння регресії в MS Excel.

Рівняння простої (парної) лінійної регресії має вигляд:

.

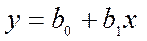Використовуючи вбудовані функції MS Excel можна отримати параметри рівняння регресії b₀, b₁:

– за допомогою матричних перетворень;

– використати статистичні функції ОТРЕЗОК, НАКЛОН;

– для знаходження обох параметрів використати с татистичну функцію ЛИНЕЙН.

– Сервис → Анализ данных → Регрессия - знаходиться стовпчик коефіцієнтів;

– або відтворити рівняння лінії тренду на діаграмі розсіювання (кореляційному полі).

Способи визначення тісноти зв’язку випадкових величин X та Y

Використовуючи вбудовані функції MS Excel можна отримати коефіцієнт кореляції r:

– використати статистичну функцію КОРРЕЛ;

– Сервис → Анализ данных → Корреляция - знаходиться кореляційна матриця.

Визначення параметрів множинної лінійної регресії

Рівняння множинної (багатофакторної) лінійної регресії має вигляд:

.

Використовуючи MS Excel можна отримати параметри рівняння регресії b₀, b₁, …, b_m:

– за допомогою матричних перетворень;

– для знаходження всіх параметрів використати с татистичну функцію ЛИНЕЙН;

– Сервис → Анализ данных → Регрессия - знаходиться стовпчик коефіцієнтів.

Класична лінійна модель множинної регресії.

Загальна лінійна економетрична модель - це регресійна модель, яка встановлює лінійну залежність між економічними показниками, один з яких є залежною (пояснюваною) змінною, а всі інші – незалежними (пояснюючими) змінними моделі.

Дата добавления: 2015-05-08