Залежна змінна для такої моделі розглядається, як ендогенна змінна, а незалежні змінні – як екзогенні

Теоретична (“канонічна”) загальна лінійна економетрична модель може бути специфікована у наступній формі:

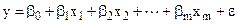, (1)

де: y – залежна (пояснювана) змінна моделі, x₁, x₂, …, x_m – незалежні (пояснюючі) змінні моделі або фактори, β₀, β₁, …., β_m – параметри моделі, ε – стохастична складова моделі, m – кількість пояснюючих змінних моделі. Зазначимо, що параметри β₁, β₂, …, β_m ще прийнято називати коефіцієнтами регресії,

Теоретична модель (1) є гіпотетичною конструкцією і дійсна, як це відмічалося у попередній темі, для всієї генеральної сукупності спостережень за змінними моделі. Невідомі параметри 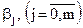цієї моделі є константами, а випадкова величина ε – взагалі неспостережувана і ми можемо зробити тільки припущення щодо закону її розподілу.

Вибіркова (емпірична) загальна лінійна економетрична модель має наступний вигляд:

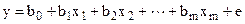, (2)

де: y – залежна (пояснювана) змінна моделі, x₁, x₂, …, x_m – незалежні (пояснюючі) змінні моделі (фактори), b₀, b₁, b_m – параметри вибіркової моделі, e – залишки моделі.

Вибіркова модель (2) є реальною конструкцією і будується на основі певної статистичної вибірки з генеральної сукупності. На відміну від моделі (1) параметри вибіркової моделі b₀, b₁, …, b_m є оцінками (наближеними значеннями) параметрів β₀, β₁, β_m і випадковими величинами, а залишки e можна оцінити (розрахувати) на основі статистичних даних. Таким чином, вибіркова модель завжди є тільки оцінкою (вдалою або невдалою) реальної але невідомої теоретичної моделі.

Вибіркова (емпірична) функція регресії для загальної лінійної економетричної моделі має наступний вигляд:

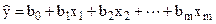, (3)

де: 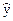– оцінка математичного сподівання залежної (пояснюваної) змінної моделі, x₁, x₂, …, x_m – незалежні (пояснюючі) змінні моделі (фактори), b₀, b₁, b_m – параметри вибіркової регресії.

Виробнича функція

Найвідомішою є двофакторна модель виробничої функції (ВФ), яка відображає залежність результату виробництва від витрат ресурсів. Під ресурсами (чинниками виробництва) найчастіше розуміють нагромаджену працю у формі виробничих фондів (капіталу) К і дійсну (живу) працю L, а під результатом – валовий випуск X, валовий внутрішній продукт Y або національний дохід N. У будь-якому разі результат стисло називають випуском і позначають Y (це може бути і валовий випуск, і ВВП, і національний дохід).

Іноді як ресурс у виробничу функцію включають залучені до виробництва природні ресурси. Якщо останні практично не змінюються, їх не слід розглядати.

Випуск продукції є функцією від витрат ресурсів (фондів і праці):

Y = F(K,L), (2.I.5)

Виробничу функцію Y = F(K,L), називають неокласичною, якщо вона гладка і задовольняє низку умов, що підлягають природному економічному тлумаченню:

1) F(0,L) = F(K, 0) = 0 – за відсутності одного з ресурсів виробництво неможливе;

2) 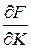> 0, >0 – із мірою зростання ресурсів випуск зростає:

3) 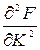< 0, < 0 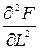– із мірою збільшення ресурсів швидкість зростання випуску гальмується;

4) F (+∞, L) = F (К, +∞) = +∞ – за необмеженого збільшення одного з ресурсів випуск необмежено зростає.

Випуск продукції моделюють за допомогою такої нелінійної ВФ:

Y = A₀K^αL^β, α >0, β >0, (2.1.6)

де А₀ – коефіцієнт нейтрального технічного прогресу; α, β – коефіцієнти еластичності за фондами та працею. Окремим випадком ВФ (2.1.6) є функція Кобба-Дугласа:

Y = AK^αL^1-α, (2.1.7)

де β = 1 - α.

Вторинні чинники можна розглядати по-різному. 3 одного боку, це чинники, що впливають на величину глобальних чинників, з іншого – на їхню ефективність. Наведемо приклад такої класифікації чинників.

Жива праця у сфері виробництва:

1. Чинники впливу на величину L:

– тривалість робочого року, тижні, дні;

– віковий склад робочої сили;

– статевий склад робочої сили.

2. Чинники впливу на продуктивність праці:

– рівень загальної освіти;

– рівень професійної освіти;

– рівень навичок (тривалість роботи за фахом);

– рівень і система оплати праці.

Виробничі фонди (колишня праця)

1. Чинники, що впливають на величину К:

– погодинне завантаження фондів і рівень використання потенційних потужностей;

– швидкість обігу фондів.

2. Чинники, що впливають на оцінку продуктивності фондів:

– технічний рівень і рівень морального зношування фондів.

– галузевий розподіл фондів.

– територіальний розподіл фондів.

– масштаби виробництва.

Розвиток чинникового підходу передбачає не так удосконалення методу виробничої функції, як поглиблену економічну й статистичну роботу.

Числові характеристики показника Y і фактора X

До числових характеристик показника Y і фактора X відносяться: мінімальна величина, максимальна величина, сумма, кількість, середне значення, добуток YX, величини дисперсії і серньоквадратичного відхилення, розхмаху варіації.

Дата добавления: 2015-05-08