Гречана Віра Василівна

Гречана Віра Василівна

Лахманюк Юлія Володимирівна

Математичні курйози та несподіванки

Роботу виконала:

Учениця 8 класу ЗШ І-ІІІ ступенів №1

м. Гайворон

Науковий керівник:

вчитель вищої категорії,

вчитель-методист,

вчитель математики НВК

«Гайворонська гімназія – ЗШ І-ІІІ

ступенів №5»

Вчитель математики:

м. Гайворон 2013-2014

ТЕЗИ

науково-дослідницької роботи

«Математичні несподіванки та курйози»

Автор: Лахманюк Юлія Володимирівна, учениця 8-Б класу ЗШ І-ІІІ ступенів №1 м. Гайворон.

Науковий керівник: учитель математики Гречана Віра Василівна, учитель вищої категорії, вчитель – методист НВК «Гайворонська гімназія – ЗШ І-ІІІ ступенів №5»

Задачі, що зв’язані із логіко-математичним мисленням відносять до нестандартних та творчих. У 2013 році Лахманюком Ю.В. зроблено 3 доповіді з даної теми під час роботи гуртка «Юний математик» у НВК «Гайворонська гімназія – ЗШ І-ІІІ ступенів №5».

Основна мета: розглянути певні методи, прийоми, алгоритми розв’язування логіко-математичних задач, названих у народі математичними фокусами та парадоксами. Розповісти про секрети та хитрості, які використані в основі цих курйозів.
Актуальність теми: незважаючи на численні публікації про захоплюючу математику та її закономірності, ця тема є найбільш складною, цікавою та важкою для засвоєння. Відомо, що рішення багатьох прикладних логіко-математичних завдань потрібні міркування та певний підхід, що розглядаються в даній роботі. Розв’язок цікавих математичних завдань стимулює розвиток пам’яті, мисленням та уваги.
Результати проведеної роботи: висвітлена більшість математичних фокусів та парадоксів, досліджені їхні секрети, історія створення логіко-математичних головоломок та вплив їх на розвиток людства. Зокрема наведені задачі практичного застосування серед публіки – цікаві та захоплюючі математичні ігри.

ЗМІСТ

ВСТУП……………………………………………………………………………..3

РОЗДІЛ І. Розвиток математичних головоломок та їх вплив на розвиток суспільства

1.1. Причини популяризації логіко-математичних завдань.

1.2. Математичні початки головоломок.

1.3. Вплив математичних головоломок на суспільство.

Розділ ІІ. Найвідоміші відкривачі та дослідники математичних курйозів.

2.1. Американець Семюель Лойд.
2.2. Головоломки Лойда.
2.3. популяризатор науки Мартін Гарднер.

2.4. Парадокс ув’язненого.
2.5. Гіпотеза Колатця

Розділ ІІІ. Власне дослідження.
3.1. Властивості чисел.

3.2. Демонстрація Чисел та їх властивостей серед публіки.

ВСТУП

В предметах навколишнього середовища ми насамперед помічаємо їх властивості, якими вони відрізняються один від одного. Через численність окремих,індивідуальних властивостей випадають з уваги загальні, притаманні геть усім предметам, і тому виявити такі властивості завжди буває важче.

Однією з найважливіших загальних властивостей усіх предметів є те, що їх можна лічити та вимірювати. Ми відображаємо цю загальну властивість предметів у понятті числа. Потреба лічити і порівнювати (вимірювати) предмети виникло в людей не відразу, а дуже давно — ще на ранньому щаблі розвитку людини, виникла в процесі її трудової діяльності. Опановували люди процес лічби, тобто поняття числа, дуже повільно, століттями, в упертій боротьбі за своє існування.

Лічби за допомогою числа тепер навчається кожна людина непомітно, ще в дитинстві,майже водночас з тим, як починає говорити, але ця звичайна для нас лічба пройшла довгий шлях розвитку і набирала різних форм. Услід за виникненням і розвитком чисел з’явилась і цікава наука про їх властивості та закони, які ними керують: «теорія чисел»

Оперуючи числами, тобто виконуючи різноманітні математичні дії, ми виявляємо не тільки їх загальні властивості,, які вивчає теорія чисел, а й особливі властивості, притаманні іноді лише невеликим групам чисел або окремим числам. Ці особливі властивості можуть і не мати великого теоретичного значення, але часто вони дуже цікаві

«Перший курйоз» заснований на теоремі Ферма. Для одного лише описи способу його демонстрації потурбувалися 13 сторінок і додатково 52 сторінки були зайняті поясненням його сутності. І хоча Пірс повідомляє про «незмінному інтересі і подиві публіки», що викликається його фокусом, кульмінаційний ефект цього фокусу представляється настільки не відповідає складності приготувань, що важко повірити, що глядачі не занурювалися в сон задовго до закінчення його демонстрації.

Копаючись у величезному масиві чисел, яких більше ніж руди в землі, мною було знайдено властивості цікаві і дивні, дивовижні та кумедні, несподівані й курйозні.

РОЗДІЛ І. Розвиток математичних головоломок та їх вплив на розвиток людства

Деякі головоломки відомі з давніх давен. Оригінальні логічні задачі знаходять на стінах єгипетських пірамід, у давньогрецьких манускриптах та інших історичних пам’ятках. Епохою розквіту у середньовічній історії головоломок можна вважати кінець ІХ століття. Ріст рівня освіченості та зниження релігіозної нетерпимості до наук призвели до розширення кола любителів логічних задач. В цей час виникла і перша книга головоломок в Європі – збірник ірландського просвітителя Алкуїна «Задачі для розвитку молодого розуму».
Найбільш широку популярність математичні головоломки отримали на межі ХІХ та ХХ столітті. Завдяки діяльності Сема Лойда та англійця Генрі Дьюдні математичні фокуси проникли до багатьох періодичних видань, стали популярними серед широких шарів населення. Ці ігри були настільки популярними, що деякі роботодавці вимушені були видати указ, згідно з яким працівникам заборонялось розв’язувати ці задачі у робочий час.
Наступним поштовхом у розвитку логічних ігр стало винайдення у 1974 угорцем Ернйо Рубиком відомого кубика. Кубик Рубика став не тільки іграшкою, але й об’єктом досліджень математиків та інженерів. З тих пір по усьому світі регулярно проводяться змагання по швидкій збірці кубика. Сучасна індустрія математичних головоломок стрімко розвивається. Постійно з’являються ноові фокуси та головоломки, видання, що покликані тримати людський інтелект у тонусі, розвивати логіку, тренувати нестандартне мисленням й покращувати інтелектуальний рівень у цілому.

Із 1992 року проводяться чемпіонати світу із пазлоспорту - інтелектуального виду змагань, у якому учасники змагаються у швидкісному розв’язуванні логіко-математичних завдань на папері.
Найбільш відомими творцями головоломок є Генрі Ернест Дьюдені, Сем Лойд, Мартін Гарднер, Ернйо Рубик.

Логіко-математичні завдання починаються з математики

Іще в давній Месопотамії, майже п’ять тисяч років тому, складали та розв’язували достатньо складні алгебраїчні задачі на знаходження невідомої величини. Пізніше у Давньому Єгипті з’явились перші задачники. Умови були прості з точки зору сьогодення, але вже тоді багато з них мали практичну основу, що що приближало математичні розрахунки до реальності.

Шотландський єгиптолог Хінд Знайшов папірус, датований ХVII століттям до нашої ери, присвячений математиці. Він уособлював собою світоч довжиною біля п’яти з половиною метрів та шириною близько п’ятнадцяти сантиметрів. Писець Ахмес стверджує, що скопіював текст з оригіналу двохсотлітньої давнини. Задача 79 із папіруса містить наступний зміст: У сіми домах тримають по сім кішок. Кожна кішка ловить по сім мишей в день, а кожна миша, якби залишилась живою, з’їла б у то й же день сім колосків пшениці. Якщо кожен колосок може дати сім гектарів зерна, скільки всього тут перечислено?
Математика формувалася нерівномірно, у різні часи в її розвиток внесли свій вклад Вавилон, Давня Греція, Китай, Індія. До речі, математика у Вавилоні мала справу не тільки із арифметикою, але й з алгеброю, серйозно переганяючи в цьому відношенні Єгипет. Цікаво, що у Вавилоні використовувалась шестерична система обрахунку.
Давньогрецький математик Діофант майже через дві тисячі років після створення папіруса Хінда запропонував таку задачу:«Знайти три числа, котрі при парному додаванні дають в сумі двадцять, тридцять і сорок».

У Європі найпершою збіркою головоломок та логічних задач стала книга «Задачі для розвитку молодого розуму» ірландського богослова Алкуїна. Вона з’явилась у другій половині ІХ століття. Написана на латині, вона вміщувала 53 задачі.
Справжньому розквіту головоломок спонукали декілька подій. По-перше, завершилась епоха релігіозного обскурантизму, а це призвело до закінчення переслідування математики, більш того, вчених-математиків перестали вважати нарівні з чорнокнижниками, заключивши договір із дияволом. По-друге, виросла загальна освіченість, що значно збільшило коло людей, зацікавлених головоломками. До того ж, тоді у Європу були завезені шахи, спричинивши імпульс винаходженню нових ігр та зв’язаних із ними логіко-математичних задач.

Вплив математичних головоломок на суспільство

Колоритною фігурою в історії головоломок став американець Сем Лойд, що жив на межі XIX - XX віків. Найвідомішим його винаходом стала головоломка "гра в п'ятнадцять", що викликала справжній ажіотаж в Америці, а потім, немов чума, перекинулася через океан і завоювала весь світ. Популярність гри була така велика, що власники фірм вивішували спеціальні оголошення, що забороняли грати з нею в робочий час. У Німеччині нею балувалися на засіданнях Рейхстагу, а у Франції їй навіть присвоїли нову назву - "такен"("задирака"), оскільки вона здавалась більш серйозною проблемою, аніж алкоголь й табак.
"Гра в п'ятнадцять" складається з п'ятнадцяти однакових плоских фішок у вигляді квадратів із стороною в одну лінійну одиницю. Усі фішки пронумеровані цифрами від одного до п'ятнадцяти і укладені у відкриту квадратну коробочку розмірами шістнадцять на шістнадцять лінійних одиниць так, що залишається вільним місце ще для однієї фішки. Будь-яку з сусідніх фішок можна пальцем пересунути на порожнє місце. Завдання полягає в тому, щоб розставити фішки рядами згідно послідовності нанесених на них номерів.
Проблема не дуже те серйозна, коли б не одна обставина. При спробі укласти фішки в коробочку випадковим чином виявляється, що лише половина з усіх можливих комбінацій піддається впорядкуванню згідно з приведеною умовою. Інші комбінації зводяться до розташування, при якому фішки від першої до тринадцятої стоять на своїх місцях, а дві фішки з номерами чотирнадцять і п'ятнадцять помінялися місцями.
Подібну комбінацію використав Лойд для рекламної компанії головоломки: за її рішення був призначений приз в декілька тисяч доларів, дуже навіть пристойна сума на ті часи. Автор нічого не втрачав, оскільки "гра в п'ятнадцять" з цієї комбінації була не вирішувана. Проте з'ясувалося це значно пізніше, після детального математичного опису властивостей головоломки.
І сьогодні індустрія головоломок продовжує бурхливо розвиватися, щорічно поставляючи на ринок усі нові книги і предмети, що дозволяють нам не просто убити час, але і в ігровій формі дати навантаження нашим логічним здібностям, навчитися нестандартно мислити і діяти.

Розділ ІІ. Найвідоміші творці та дослідники математичних курйозів.

Американець Семюель Лойд

Семюель Лойд старший (1841-1911) – американський журналіст, шахіст, найвідоміша журналістська постать у ХІХ столітті.
Лойд-старший народився в 1841 році у Філадельфії у "заможних, але чесних батьків"(власне вираження Лойда).
У 1844 році його батько, агент з продажу нерухомого майна, перевіз сім'ю в Нью-Йорк, де Сем до 17 років відвідував загальноосвітню школу. Якби молода людина закінчила коледж, то з нього цілком міг би вийти видатний математик або інженер.

Але Сем не став поступати в коледж. Причиною тому значною мірою явилися шахи.
Впродовж десяти років Лойд тільки і робив, що пересував по дошці шахові фігури. У той час шахи були незвичайно популярні; багато газет вели шахові відділи, де поміщалися завдання, придумані читачами. Перше завдання Лойда було опубліковане однією нью-йоркською газетою, коли авторові було всього 14 років. Упродовж наступних п'яти років він настільки продуктивно вигадував шахові головоломки, що став дуже відомий у шаховому світі. У 16 років Лойд став редактором відділу завдань в Chess Monthly("Шаховий щомісячник"), який тоді видавали Д. У. Фіск і молодий шаховий майстер П. Мерфи.
Пізніше Лойд редагував шахові відділи в одних газетах і під різними псевдонімами регулярно посилав придумані ним завдання в інші.

У 1877-1878 роках Лойд вів щотижневу шахову сторінку в додатку до журналу Scientific American. Кожна його стаття розпочиналася із заголовної букви, складеної з шахових фігур завдання. Ці сторіночки увійшли до книги Лойда "Шахова стратегія", яку він власноручно набрав і надрукував. Книга Лойда, що містить 500 його обраних завдань, і понині має величезний попит.

Головоломки Лойда

Частіше за інших передруковувалося завдання Лойда, яке він придумав в 18-річному віці. Це завдання може служити прекрасною ілюстрацією до уміння Лойда вдягатися найскладніші питання у форму анекдота.
У 1713 році шведський король Карл XII разом зі своїм військом був оточений турками під Бендерами. Не звертаючи уваги на кулі і ядра, король з одним зі своїх міністрів часто грав в шахи. Одного разу, коли у них виникла позиція, зображена на мал. 40, Карл, що грав білими, оголосив супротивникові мат в три ходи. У цей момент очманіла куля збила з дошки білого коня. Карл уважно вивчив нову позицію, посміхнувся і сказав, що коня йому і не треба, оскільки і без коня він може поставити супротивникові мат в чотири ходи. Ледве він встиг це сказати, як друга пуля збила з дошки білого пішака h2. Карл незворушно оглянув фігури, що залишилися на дошці, і оголосив супротивникові мат в п'ять ходів.

У цієї історії є продовження. Через декілька років після появи завдання Лойда один німецький шахіст помітив, що якби перша куля збила замість коня білу туру, то Карл все одно міг би оголосити мат в шість ходів. Читачі, що захоплюються шахами, напевно, із задоволенням розміркують над цим чудовим "чотирьохсерійним" завданням.
Відповідь: У шаховому завданні "білі" оголошують мат в три ходи, узявши пішака турою. Якщо чорний слон візьме туру, то білі перекладуть свого коня на f3, тим самим змушуючи чорних переставити слона. Тоді білі оголошують мат, роблячи хід пішаком на g4. Якби чорні узяли замість тури коня, білі оголосили б шах турою Лh3+, чорні в цьому випадку прикриваються слоном(Ch4), а білі, як і раніше, оголошують пішаком мат на g4.

Після того, як куля збила білого коня, білі, узявши чорного пішака пішаком, оголосять мат в чотири ходи. Якщо чорні зроблять хід слоном СеЗ, то білі дадуть відповідь турою Лg4. Далі слідує хід чорного слона Cg5 і хід у відповідь білою турою Лh4+ (шах). Чорний слон бере туру, а білі оголошують мат пішаком на g4.

Після того, як куля збила з дошки білого пішака Н2, білі оголошують мат у п’ять ходів, роблячи перший хід турою. Лb7. Якшо наступить хід чорних СеЗ, то 2. Лb1 Cg5; 3. Лh + Ch4; 4. Лh2!! gh; 5. g4x (мат).

Якщо ж чорні роблять перший відповідний хід слоном Cg1, то слідує: 2. Лb1 Ch2; 3. Ле1 Kph4; 4. Kpg6. На будь-який хід чорних білі відповідають:5. Ле4х (мат).

Якби першою кулею була збита біла тура, а не кінь, білі оголосили б мат в шість ходів, починаючи гру конем(Kf3). Тоді кращим ходом чорних був би хід слоном Ce1, який привів би до такого продовження: 2. K: el Kph4; 3. h3 Kph5; 4. Kd3 Kph4; 5. Kf4 h5; 6. Kg6x(мат).
Перша головоломка, що принесла комерційний успіх, була придумана Лойдом, коли йому ще не виповнилося і двадцяти років. Вона зображена на мал. 41 точно у такому вигляді, як її намалював Лойд.

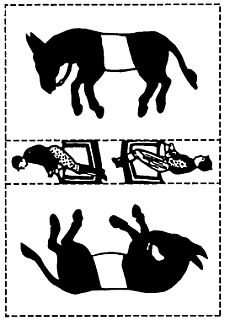
Розрізавши картинку уздовж пунктирних ліній і переставивши її частини(не згинаючи їх при цьому), ми побачимо наїзників, що сидять верхи на ослах. П. Т. Барнум придбав у Лойда право видання декількох таких картинок і випустив їх в продаж мільйонними накладами під назвою "П. Т. Барнум і його чарівні ослики". Говорять, що за декілька тижнів ця головоломка принесла Лойду 10000 доларів. Не втратила вона своєї популярності і в наші дні.
З точки зору математики найцікавішим винаходом Лойда слід вважати гру п'ятнадцять. У кінці сорокових років нашого століття інтерес до гри в п'ятнадцять поновився, коробочку з 15 квадратними шашками і зараз ще можна зустріти в магазинах іграшок.

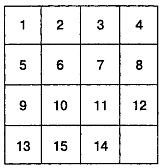
У коробочці можуть вільно переміщатися 15 перенумерованих квадратних шашок. Два останні квадрати переставлені. Вимагається, не виймаючи з коробочки, пересунути квадрати так, щоб їх номери розташувалися по порядку, а порожній квадрат опинився в правому нижньому кутку. У сімдесятих роках минулого століття гра в п'ятнадцять була у великій моді, їй присвячувалися навіть наукові статті в математичних журналах.

За правильне рішення головоломки Лойд призначив премію в 1000 доларів. Десятки сотень людей присягалися, що вони вирішили завдання, але жоден так і не зміг згадати ходи, щоб записати їх і отримати за це премію. Призначаючи премію, Лойд нічим не ризикував, бо запропоноване ним завдання нерозв'язне. Із понад 20 мільярдів всіляких розташувань квадратів рівно половину комбінацій можна отримати, пересуваючи квадрати з початкового розташування, показаного на маюнку. Інші розташування квадратів, у тому числі і те, яке вимагається знайти, якщо скористатися термінологією теорії перестановок, мають іншу "парність", а перестановки, що мають різну парність, не переходять один в одного при переміщенні квадратів усередині коробочки.
Можна грати і по-іншому: безладно скласти квадратики в коробочку і, пересуваючи, намагатися розташувати їх по порядку номерів. Вірогідність успіху, очевидно, дорівнює 1/2. Існує простий спосіб, що дозволяє дізнатися, чи можна отримати цю перестановку з будь-якої іншої перестановки А: для цього треба лише підрахувати число "транспозицій"(кожна транспозиція означає перестановку двох квадратів: їх треба вийняти з коробочки і поміняти місцями), які необхідно вчинити, щоб перетворити А у В. Якщо це число парне, то А і В мають однакову парність і тоді, пересуваючи квадрати, А можна переводити у В і навпаки.

Та обставина, що транспозиція двох квадратиків автоматично міняє парність перестановки їх номерів, покладена в основу одного досить злого завдання-жарту(різновиди гри в п'ятнадцять), випущеного в продаж декілька десятків років назад. На квадратиках, як показано на мал. 43, написані не цифри, а букви. На квадратах одного кольору(у нас вони заштриховані) написані слова RATE і YOUR, на квадратах іншого кольору слова MIND і PAL. Ви показуєте квадрати з написом, що вийшов на них, своїй жертві і потім перемішуєте їх як завгодно. При цьому ви непомітно заганяєте друге R в лівий верхній кут. Ваша нещасна жертва, звичайно, залишить букву R в лівому верхньому кутку і намагатиметься розташувати по порядку інші букви.
Це завдання безнадійне, тому що, помінявши місцями букви R, ви змінили парність перестановки. У кращому разі бідолаха зможе отримати "RATE YOUR MIND PAL" (подумай-но мізками, приятель).
З усіх головоломок Лойда найбільшою популярністю, поза сумнівом, користувалася його загадкова картинка "Таємниче зникнення", запатентована їм в 1896 році. Картонний круг в центрі прикріпляється до картонного квадрата. По колу намальовані 13 воїнів, частково - на крузі, частково - на квадраті.

Якщо круг трохи повернути, частини воїнів з'єднаються вже іншому, а один воїн зовсім зникне! Цю головоломку неодноразово публікували, тому на мал. 44 показана менш популярна, але в якомусь сенсі цікавіша загадкова картинка, яка називається "Тедді та леви". У одному положенні круга ви бачите сім левів і сім мисливців, а в іншому - вісім левів і шість мисливців. Звідки береться восьмий лев? Хто з мисливців зникає і куди він дівається?
Відповідь: коли частини зміщуються, зникають усі леви і мисливці, а замість них з'являються вісім нових левів, кожен на 1/8 менше за первинний, і шість нових мисливців, кожен на 1/6 більше за колишній.

У 1914 році, через три роки після смерті батька, Лойд-молодший видав велетенську "Енциклопедію головоломок", в якій була зібрана, поза сумнівом, найбільша колекція завдань, що коли-небудь з'являлася в одній збірці.

Популяризатор науки Мартін Гарднер

Мартін Гарднер (1914-2010) – американський вчений, журналіст періодичного видання “Scientific American”, а також письменник.

Мартін Гарднер народився і виріс в околицях Талса, Оклахома, США. Він відвідував коледж університету Чикаго, де отримав ступінь бакалавра філософії[2]. Під час Другої світової війни декілька років служив у ВМФ США в якості корабельного секретаря(йомен) на борту ескортного міноносця USS Pope в Атлантичному океані. Його корабель знаходився в океані у момент закінчення війни і капітуляції Японії в серпні 1945 року.
Після війни Гарднер знову відвідував університет Чикаго[3]. Впродовж року також вчився в магістраті, але так і не захистив наступну міру.

На початку 1950-х Гарднер був редактором журналу Humpty Dumpty і писав нариси і історії для декількох дитячих журналів[4]. Його завдання по згинанню паперу привели до роботи в Scientific American[5].

У 2002 році Мартін Гарднер повернувся в Норман(Оклахома), де його син, Джеймс Гарднер, працював професором педагогіки в університеті Оклахоми(англ.).

Мартін Гарднер помер 22 травня 2010 року в Нормані.

Завдяки йому людство дізналось про про флексагони, пошук фальшивих монет, парадокс ув’язненого, проблемі 3х + 1. Розберемо дещо з них./

ПАРАДОКС УВ’ЯЗНЕНОГО

В'язень, засуджений до вищої міри покарання, одного разу в неділю був викликаний до начальника в'язниці(чесній людині, що ніколи не обманює навіть найзліших ворогів суспільства). Начальник сказав: "Вас страчують наступного тижня, але в який саме день, я вам не скажу. Ви дізнаєтеся про це тільки уранці в день страти".

Через деякий час в'язень набув здатності нормально роздумувати. Він негайно зробив висновок, що страчувати в наступне воскресіння його не можуть: адже тоді ще в суботу увечері буде ясно, що для страти залишився один-єдиний можливий день. Це означатиме, що в'язневі став відомий день страти ще до настання цього дня, а такого не може бути за визначенням - адже начальник ніколи не бреше!
"Іншими словами, останній можливий день для моєї страти, - думав в'язень, - це субота. Але тоді якщо мене не страчують в п'ятницю уранці, то до вечора п'ятниці я теж точно знатиму день, коли мене повинні страчувати. Проте начальник сказав, що про день страти я дізнаюся лише уранці, а не напередодні увечері, - значить, і в суботу мене не можуть страчувати теж".
Послідовно міркуючи, нещасний виключив з розгляду п'ятницю, четвер, середовище, вівторок і понеділок. У результаті він дійшов висновку, що його взагалі не можуть страчувати, оскільки ні для одного дня тижня умови, сформульовані начальником в'язниці, не виконуються.

Звичайний виклад цієї історії - "парадоксу в'язня" - на цьому і закінчується. Парадокс тут в тому, що начальник, що завжди говорить правду, формулює припис про страту, виконати яке неможливо із-за його суперечності. Чи все-таки можливо?
В середу вранці ув'язненому, вже упевненому у своїй безкарності, повідомили, що сьогодні його страчують. Це стало для нього повною несподіванкою - і означає, умова начальника виявилася виконаною.

Виходить, що нездійсненний припис виявився можливим виконати саме із-за його нібито нездійсненності! Як?

Думка перша

Одне з перших же питань, на які доводиться відповідати: чи можна вважати, що начальник сам призначає день страти? Можна сказати, що так. А можна і сказати, що це робить за нього комп'ютер. Так і зробимо: щоб не обговорювати стратегії поведінки начальника в'язниці, вважатимемо, що день страти він дізнається по датчику випадкових чисел. Можливі значення датчика - від 1(понеділок) до 7(воскресіння). Крім того, оскільки число днів в тижні не грає особливої ролі, то можна відразу узагальнити парадокс на випадок N можливих днів страти і досліджувати його при різних N
При N=1 парадокс дуже простий. Начальник говорить буквально наступне: "Вас страчують завтра, але до завтрашнього ранку ви нічого про це не дізнаєтеся". Це твердження суперечливе саме по собі, тому ніякій інформації в'язень з нього винести не зможе. Суперечливі твердження не можуть бути ні істинними, ні неправдивими. Інакше кажучи, з усієї інформації парадоксу можна зробити тільки один висновок: начальник в'язниці не завжди говорить правду.

Найцікавіше розглянути випадок N=2. Повторимо міркування ув'язненого саме в цьому випадку: "Мене не можуть страчувати у вівторок, оскільки інакше я дізнався б про це до вечора понеділка. Але тоді мене повинні страчувати в понеділок, і я знаю про це вже зараз. Це суперечить затвердженню начальника про те, що я не повинен упізнати дату страти до її настання". Далі ув'язнений вирішує, що начальник збрехав йому. І тільки уранці в того з двох днів, на який вкаже комп'ютер, виявляється, що начальник сказав правду.
У чому тут протиріччя і в чому помилка - в міркуваннях в'язня або в початковому затвердженні начальника в'язниці?

Думка друга

Практично усі, хто стикається з парадоксом саме в такій формі, вважають суперечливою умову, сформульовану тюремником. Проте на прохання вказати на це протиріччя починають повторювати саме міркування в'язня! Але раз міркування в'язня приводять до парадоксу, то вони не можуть бути використані для пояснення цього парадоксу! Чим же все-таки пояснюється протиріччя, що виходить? В'язня не можуть страчувати, не порушивши припису, - і все-таки страчують.
Я пропоную читачам доки подумати над цим самостійно. А також - над різницею між цим варіантом парадоксу і тим, коли начальник сам(без допомоги комп'ютера або якогось іншого датчика випадкових чисел) призначає день страти.

А тепер - рішення. Точніше, одне з можливих рішень.

Начальник стверджує, що звістка про страту буде для засудженого несподіваною. У якому сенсі потрібно розуміти цю "несподіванку"? Очевидно, в тому, що в'язень не зможе точно передбачити день своєї страти. Але скільки разів в'язневі дозволяється робити таке пророцтво? Якщо ми проаналізуємо міркування в'язня, то побачимо, що він робить багатократні пророцтва про день страти і міняє їх у тому випадку, якщо попереднє пророцтво виявилося неправдивим. Але ж такий процес передбачення явно не передбачався начальником в'язниці!
Якщо ж розуміти затвердження начальника так, як він його і формулював - що в'язневі дозволяється зробити пророцтво тільки один раз(наприклад, назвати дату своєї страти до настання понеділка), то у ув'язненого немає ніякої можливості точно упізнати цю дату заздалегідь. Його можуть страчувати або в понеділок, або у вівторок - в повній відповідності з інформацією, повідомленою начальником в'язниці.

Парадокс створюється саме із-за неповноти умови, а також із-за двоїстості інтерпретації поняття "Очікувана дата страти".

Думка третя

Уявіть собі, що дату страти вибирає сам начальник в'язниці. Тоді для N=2 міркування в'язня бездоганні і, отже, умови завдання суперечливі. Так? А що виходить для N=7 або N=1998? Чи як і раніше завдання визначення дня страти, поставлене начальником перед ув'язненим, позбавлене сенсу? Или вже немає? І якщо ні, то при якому конкретному N відбувається перехід від першої ситуації(суперечність і безглуздя умови) до другої(умова коректна, а міркування в'язня помилкові)?
Припустимо, що для N - 1 завдання ще суперечливе, а для N - вже ні. Якби начальник вибрав будь-який з днів від другого до N- го, то у нього була б усього N - 1 можливість. Значить, в цьому випадку завдання було б суперечливим. А раз ми припустили, що це не так, то начальник повинен вибрати для страти тільки перший день! І це вже відомо в'язневі, що знову-таки робить завдання суперечливим.

ГІПОТЕЗА КОЛАТЦЯ

Мартін Гарднер писав у своїх статтях багато про математичні закономірності та малозрозумілі проблеми. Одна з таких проблем є «Гіпотеза Колатця», у подальшому названа просто «проблема 3х + 1». Ця гіпотеза була запропонована у 1937 році Лотаром Колатцем, що й назвав її на свою честь.
Над цією проблемою думали математики із кращих університетів світу, потрачено багато годин машинного часу. Для пояснення суті гіпотези розглянемо наступну послідовність чисел, що називається сіракузькою послідовністю. Беремо будь-яке натуральне число n. Якщо воно парне, то ділимо його на 2, а якщо непарне, то множимо на 3 і додаємо 1(отримуємо 3n + 1). Над отриманим числом виконуємо ті ж самі дії, і так далі. Завдання цієї проблеми стоїть так: дізнатись, чи є таке число, почавши з якого не закінчаться розрахунки одиницею?
Сучасна математика не в силах дати відповідь на таке, здавалося б, просте питання. Навіть нещодавно доведена велика теорема Ферма - і та формулюється з використанням піднесення до степеня і цілих чотирьох змінних. А для завдання 3x+1 на сьогодні достовірно відомо, що послідовність приходить в одиниці для усіх не більше ніж девятнадцатизначных чисел, але в загальному випадку це нічого не доводить. Є навіть припущення, що проблема 3x+1 - одно з так званих "недоказовних" тверджень, існування яких виходить з теореми Геделя про неповноту.
Проте простежити за поведінкою окремих чисел при такому перетворенні - cама по собі цікава математична розвага. Беремо число і починаємо з нього за приведеним правилом починаємо отримувати наступні. Попутно можна помічати, до якого максимуму вдалося піднятися і скільки кроків доведеться зробити, поки не прийдемо до одиниці.
У своїх роботах Гарднер брав 2 найкращих для цього числа – 3 та 27.

Для числа 3 отримуємо:

3 - непарне, 3×3 + 1 = 10

10 - парне, 10: 2 = 5

5 - непарне, 5×3 + 1 = 16

16 - парне, 16: 2 = 8

8 - парне, 8: 2 = 4

4 - парне, 4: 2 = 2

2 - парне, 2: 2 = 1

1 - непарне, 1×3 + 1 = 4

Очевидно, що, починаючи з 1, починають циклічно повторюватися числа 1, 4, 2.
Для числа 27 отримуємо:

27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1,.

Послідовність прийшла до одиниці тільки через 111 кроків, досягнувши в піці значення 9232.

Гіпотеза Колатца полягає в тому, що яке б початкове число ми не узяли, рано чи пізно ми отримаємо одиницю.

Розділ ІІІ. Власне спостереження.

Властивості чисел

Майже у всьому світі користуються тепер єдиною системою

чисел: десятковою. У цій системі вживається десять цифр: 1, 2, 3, 4, 5, 6, 7, 8, 9 і 0, і цих цифр досить,щоб записати будь-яке число.

Для прикладу, утворімо найбільше десятицифрове число з усіх десяти цифр, застосовуючи звичайну, загальноприйняту форму записування числа.

Ось воно:

Усяке представлення цифр у цьому числі приведе безпосередньо до меншого числа.

Для подальших спостережень над курйозними властивостями чисел виберемо 2 числа:

а=123456789 b=987654321

n найменше й найбільше з дев’ятицифрових чисел без нуля, в яких цифри не повторюються.

Різниця b-a складається з тих самих цифр:

987 654 321 – 123 456 789 = 864 197 532

Помічаємо, що цифри не повторюються.

Якщо а помножити на 8 і додати 9, то дістанемо b:

123 456 789х8+9=987654321

Демонстрація чисел та їх можливостей серед публіки

Задумане число

З сірникової коробки приберіть частину сірників. Запропонуйте бажаючому з глядачів задумати будь-яке число з другого десятка. Цифри цього числа нехай складе між собою. Коли вам назвуть результат, така кількість сірників поверніть назад у коробку.

Якщо тепер глядач перерахує в коробці все сірники, то їх кількість буде дорівнює задуманому числу.

Секрет фокусу: У коробці потрібно залишити дев'ять сірників - решта сірники забираються. Яке б число не задумали глядачі, сума його цифр (якщо до неї додати 9) дорівнюватиме задуманому числу. Наприклад: задумали число 17. 1 + 7 = 8. Вісім сірників поверніть назад у коробку. 9 + 8 = 17.

Швидше калькулятора

Запросіть двох глядачів на змагання в швидкому рахунку. Повідомте, що на вашому боці - надприродні здібності, на боці глядачів - калькулятори. І тим не менше ви встигнете зробити обчислення першим.

Назвіть для стислості першого глядача гравцем А, а другий - гравцем Б. Передайте їм папір і олівці і попросіть написати на листках літери А і Б на відстані приблизно 2,5 см один від одного; на своєму листку зробіть те ж саме:

А -Б

Попросіть гравця А назвати будь-яке тризначне число, що складається із різних цифр, наприклад 625. Потім всі троє розпишіть його під літерами:

А Б

625 625

Тепер попросіть гравця Б назвати інше тризначне число, також складається з різних цифр, - нехай це буде 784. Знову всі разом розпишіть це число (кожен на своєму листку паперу), але тільки в колонці А:

А Б

625 625

Скажіть, що вам не хотілося б відставати від них, і ви теж запропонуйте своє число. Обом противникам воно здасться випадково вибраним, однак насправді це не так. Перед тим як його назвати, швидко зробіть в розумі віднімання - від числа 999 відніміть то, яке назвав гравець Б (999 - 784 = 215), і отримане число повідомте гравцям. Попросіть їх записати цей результат під першим числом в колонці Б. Після цього переходите до змагання в швидкому рахунку:

А Б

625 625

Передайте гравцям А і Б по калькулятору. Поясніть, що просите перемножити два числа, записані в їх колонках, а потім скласти обидва твори. Вам же доведеться вчинити ці арифметичні дії в думці. Коли обидва гравці зрозуміють, що від них вимагається, по команді займіться обчисленнями.

Секрет фокуса полягає в тому, що ви самі зможете підрахувати число дуже швидко. Для цього відніміть одиницю від першого числа (625) і впишіть результат (624); після цього відніміть його від 999: 999 - 624 = 375 і впишіть його поруч з першим. Це число і є шукане! У вас обчислення займають лічені секунди, тоді як ваші гравці будуть значно довше возитися з розрахунками:

А Б

625 625

Безпомилковий поворот

Написавши на листку паперу довгий ряд чисел - до 20-25, заявіть, що можете безпомилково повторити весь ряд, число за числом. І дійсно, виконуєте це блискуче, незважаючи на те що в послідовності цифр не помітно жодної закономірності.

Секрет фокуса досить простий - до смішного: ви пишете підряд кілька телефонних номерів ваших знайомих.

Співпадаюче число

Передайте глядачеві папірець і скажіть, що на ній ви написали число, воно не менше 1 і не більше 50. І нехай він, не дивлячись на цей папірець, покладе її в кишеню. Коли глядач сховає папірець, нехай візьме інший клаптик і напише на ньому яке-небудь число від 50 до 99 так, щоб ви не бачили.

Тепер скажіть йому одне число, яке він повинен додати до свого числу, закреслити першу цифру результату зліва і додати її до того, що у нього вийде. Після цього запропонуйте йому відняти свій результат з того числа, яке він задумав, і подивитися, що написано на вашій папірці. На ній буде стояти те ж саме число.

Секрет фокусу: На папірці, яку глядач, не дивлячись, сховав у кишеню, ви написали, наприклад, число 23 (незгірш 1 і не більше 50). Коли глядач задумає число (від 50 до 99), яку ви не знаєте, назвіть йому число 76 і нехай додасть його до свого числу. Число 76 ви взяли не навмання - в ​​цьому вся хитрість.

Ви відняли написане вами число 23 з 99 і отримали 76. Якби ви написали на папірці не 23, а, скажімо, 40, ви веліли б глядачеві скласти з його числом не 76, а 99 - 40, тобто 59. І потім у відповіді у нього вийшло б 40, скільки б він не задумав.

Припустимо, глядач задумав 92. Скажіть йому додати до його числу 59. Коли глядач складе числа, він отримає 151. Закреслить першу цифру ліворуч - отримає 51. Додасть закреслити цифру - отримає 52. Відніме цей результат з свого задуманого числа: 92 - 52 = 40.

Шість підходящих цифр

На шести листах паперу так, щоб не бачили глядачі, напишіть шість різних чисел. Скажіть глядачам, що, яке б тепер число від 1 до 60 вони ні назвали, ви складіть його з тих чисел, які написані на листках.

Яке б число після цього ні називали глядачі, викладайте ті чи інші листки, і сума їх буде відповідати названому числу, хоча скласти з шести чисел цілих шістдесят здається завданням нездійсненним.

Секрет фокуса: Насправді завдання цілком здійсненне. На шести листках вами були написані числа: 1, 32, 4, 8, 16, 2. Яке б тепер число від 1 до 60 ні назвали глядачі, вам легко буде викласти необхідну число. Назвали, наприклад, 51. Викладіть листки 32, 16, 1, 2, вийде 51. Або, наприклад, назвуть 27: 1 + 8 + 16 + 2 = 27 і т. д.

ВИСНОВКИ

Світ чисел глибоко проникає у наше життя. Вони є скрізь: на предметах побуту, у техніці, на робочому місці. Без них мало хто уявляє своє життя. Але ми часто не помічаємо всіх тих властивостей, що можуть нам показати й навчити нас чогось нового числа.

Досліджуючи числа, науковці знаходять небачені раніше їхні властивості. Для людства відкриваються нові нонсенси та парадокси. Деякі курйози, виявлені століття тому, й досі не під силу розв’язати найкращим розумам планети, але вирішуючи ці проблеми, людина рухається вперед до прогресу.

Уже зараз, завдяки диво-властивостям світу чисел, ми можемо демонструвати всю хитрість та швидкість свого розуму. Дуже доречно тут звучатиме цитата французького фізика й математика Блеза Паскаля: «Предмет математики настільки серцозний, що потрібно не втрачати нагоди зробити його трішки захоплюючим».

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ

1. Кемені Дж. Д., Снел Дж., Томсон Дж. Л. «Введення в кінцеву математику». – М.: ІЛ, 1963.
2. С. Лойд (мол.), С. Лойд (ст.) «Енциклопедія головоломок». – М.: Мир, 1970.
3. Лойд С. (ст.) «Математична мозаїка» - М.:Мир, 1980.
4. Брукс А. «Логіка фіксованих та зростаючих автоматів» - Технічний Дослідницький Інститут Університету Мічигану, 1961
5. Б. Хеєс «Зльоти та падіння чисел-градин», Scitntific American: №3 березень 1984.
6. Лєбедєв Ю.А. «Про деякі евретичні аспекти послідовності («3n+1» - проблеми в теорії чисел)» - М.:Мир, 1998

Дата добавления: 2015-05-07