Поняття про напруження

Для прогнозу поведінки грунтової основи необхідно порівняти величину навантаження і здатність грунтової основи його витримати. Мірилом перевірки є величина напруження – інтенсивність розподілу сил по певному перерізу. Інтенсивність напруження графічно відображають за допомогою епюр. Напруження в грунтовій товщі визначається величинами зовнішніх і внутрішніх сил. Для визначення величин внутрішніх сил використовують метод перерізів. Зовнішні сили за характером дії можна поділити на: зосереджені і розподілені. Зосереджені – сили, що діють на невелику частину поверхні тіла. Напруження в дослідній точці змінюється за законом еліпса: найбільша вісь еліпса проходить вздовж бісектриси кута бачення, а найменша вісь перпендикулярна їй. Найбільше і найменше напруження в дослідній точці називається головними напруженнями. Напруження в дослідній точці можна розрахувати знаючи головні.

6.Метод перерізів. Епюри напружень.

Метод перерізів використовують для визначення величин внутрішніх сил. Переріз може мати будь-який напрямок (вертикальний, горизонтальний, похилий). При цьому уявляємо, що на одну частину тіла під перерізом діє не друга частина тіла, а певна сила. Внутрішні сили відображають зв'язок між окремими частинами тіла і визначаються фізичними властивостями досліджуваного тіла. Величини внутрішніх сил не залишається постійними і змінюються в залежності від величин навантаження, або іншого виду зовнішніх сил. Положення перерізу у просторі прийнято визначати кутами нахилу нормалі цього перерізу до напрямку координатних вісей. Напрямок дії сили і розташування перерізу можуть мати кілька варіантів:

· сила діє перпендикулярно перерізу

· у випадку коли вертикальна сила діє на похилий переріз, напруження зменшиться тому, що дослідна площа збільшиться.

Дія сумарного вектору на похилий переріз може бути розкладена на частини правилу паралелограма.

Інтенсивність напруження графічно відображається за допомогою епюр напружень.

7.Поняття про напружений стан тіла.

Сукупність напружень, що діють в усіх площинках, проведених через точку, називається напруженим станом. Напружений стан в точці повністю визначається напруженнями по трьох взаємно перпендикулярних площинках. Тобто за цими напруженнями можна визначити напруження в будь-якій площинці, проведеній через цю точку.

По кожній з трьох взаємно перпендикулярних площинок діють три напруження: нормальне і дві складові дотичного напруження, паралельних відповідним координатним осям. Ці дев’ять напружень, записані у вигляді квадратної матриці (у кожному рядку – напруження по одній з площинок, у кожному стовпчику – напруження, що діють паралельно одній з координатних осей)називаються тензором напружень.

В околі довільної точки деталі при довільному навантаженні можна виділити, принаймні, один елемент у вигляді прямокутного паралелепіпеда, гранями якого є площинки, де відсутні дотичні напруження. Такі площинки називаються головними, а нормальні напруження в цих площинках – головними напруженнями. Головні напруження мають властивість екстремальності. Одне з них є найбільшим (в алгебраїчному розумінні) напруженням з усіх можливих, друге – проміжним, третє – найменшим.

8.Нормальні та дотичні напруження.

Дія сумарного вектору на похилий переріз може бути розкладена на частини по правилу паралелограма.Складовий вектор напружень, направлений перпендикулярно.виражає опір внутрішніх сил при стисканні і називається нормальним напруженням. Складовий вектор,що лежить у площині перерізу виражає опір внутрішніх сил здриганню і називається дотичним(тангенційним). σn=σα cosα=σ α

τ= σα*sinα= sin 2α

σn→max при α→0(τ=0)

τ→max при α= ±

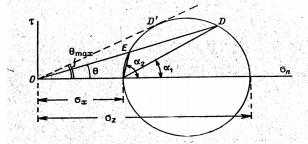
дотичні напруження дорівнюють нулю при будь-яких значеннях кута α. В інших випадках величина головних напружень безперервно змінюється зі зміною місцеположення дослідної точки в ґрунтовій основі споруди. Напрям дії більшого головного напруження співпадає з бісектрисою кута бачення.

9. Головні напруження (плоска задача).

Поняття головних напружень використовується для характеристики зміни величини напруження у будь-якій точці грунтової основи (в межах активної зони) за певними правилами. Величина цих напружень не залежить від властивостей грунтів, а залежить від величини питомого навантаження споруди, відстані дослідної точки від фундаменту і розташування у межах активної зони (під центром споруди).

Напруження в дослідній точці змінююється по закону Еліпса. Найбільша вісь еліпса проходить вздовж бісектриси кута бачення, а найменша вісь, препендикулярна їй. Чим ближче дослідна точка до фундаменту, тим більші вісі еліпса, і навпаки.

Найбільше і найменше напруження в дослідній точці назив. головними напруженнями.

Плоска задача застосовується у тих випадках, коли проектується споруда значної довжини і малої ширини. Інколи розглядається кілька дослідних перерізів і таким чином вивчаємо поле напружень для значної полощі.

Умови плоскої задачі мають місце у випадках, коли напруження розподіляється у одній площині, а напрямку перпендикулярному вони або рівні нулю, або постійні. Ця умова має місце для дуже витягнутих споруд (стрічкових фундаментів, основ підпірних стінок тощо).

10. Розподіл напружень у випадку плоскої задачі. Кола напружень Мора.

Умови плоскої задачі мають місце у випадках, коли напруження розподіляється

у одній площині, а напрямку перпендикулярному вони або рівні нулю, або постійні.

Ця умова має місце для дуже витягнутих споруд (стрічкових фундаментів, основ

підпірних стінок тощо).

Використовуючи формули для визначення напружень в лінійно деформованому

масиві від погонного навантаження (Фламана) в умовах плоскої задачі шляхом

інтегрування напружень від дії елементарних сил. Отримують вирази для складових

напружень для різних видів розподілених навантажень: рівномірної, зростаючої по

закону прямої тощо.

Схема дії рівномірно розподіленого навантаження в умовах плоскої задачі

показана на рис.

Напруження в дослідній точці на різних перерізах легко визначити за допомогою кругів Мора. Діаметр яких дорівнює різниці головних напружень. Вертикальна вісь відображає зміни вертикальних напружень. Для визначення напружень на кожному перерізі, що проходить через дослідну точку, необхідно в точці А відобразити кут α. З точки Д на крузі опускаємо перпендикуляр на вісь і отримуємо значення нормального і тангенціального напруження.

11. Історія розвитку уявлень про розподіл напружень в ґрунтових масивах

Становлення механіки ґрунтів, як науки, починається з першої фундаментальної праці К.О.Кулона (Франція,1773),в якій він запропонував визначення напруження в сипучих грунтах через питоме навантаження і кут внутрішнього тертя.

1798 рік робота Фукса. За його теорією осідання ґрунтової основи має місцевий характер (активна зона має ширину фундамента, напруження в активній зоні залиш однаковим, деформації є незворотніми)

Вінклер у своїй теорії вказав на можливість пружного відновлення деформ, але при зберіганні суто місцевого характеру.

Соколовським була запропонована ідея про межі стислої зони для сипучих грунтів. (його ідея не є достатньо точною)

У 1885 році була опублікована праця Ж.Бусінеска „ Про розподіл напружень у пружних ґрунтах від зосередженої сили „, яка стала базовою теорією для вивчення напруженого стану ґрунтової товщі. Задача вирішена у полярних координатах. Важливим етапом у розвитку механіки ґрунтів стали дослідження К.Терцагі, викладені в книжках „ Будівельна механіка ґрунту на основі його фізичних властивостей”,1925, та „Теоретична механіка грунтів”,1943. Значну роль в розробку теоретичних положень тазастосування механіки ґрунтів в практику будівництва відіграли роботи М.М.Маслова, М.А.Цитовича (1934 – перший курс лекцій), Єгорова, Симвуліді.

12. Напруження суцільного напівпростору від дії зосередженої сили (просторова задача).

На сьогодні строге рішення цієї задачі отримане лише для прямокутної ділянки завантаження, деформації якої відповідають деформаціям поверхні лінійно деформованого напівпростору, тобто для умов вельми гнучкого передавання навантаження.Визначення стискаючих напружень під прямокутною ділянкою завантаження виконується за методом кутових точок, який дозволяє дуже швидко розрахувати стискаюче напруження для точок, що знаходяться на вертикалі під центром та кутами завантаженого прямокутника зі сторонами l та b, які називаються кутовими.

Метод кутових точок для визначення величин стискаючих напружень в різних точках простору ґрунтової основи під дією рівномірно розподіленого навантаження застосовують в тому випадку, коли завантажена площина може бути розділена на прямокутники так, щоб дослідна точка стала кутовою. Тоді величина стискаючого напруження в цій точці (для горизонтальних рівнів, паралельних плоскій межі грунтового простору) буде дорівнювати алгебраїчній сумі напружень від прямокутних площин завантаження, для яких ця точка є кутовою.

В розрахунках стискаючих напружень для будь-якої точки простору ґрунтової основи використовуються кутові коефіцієнти _о та _с .

Під центром завантаженого прямокутника максимальне стискаюче напруження розраховується за формулою: ; а для точок під кутом завантаженого прямокутника: ;

13Визнвчення стискаючих напружень від дії зосередженої сили та суми зосереджених сил

. Процедура розрахунку напружень від дії зосередженого навантажень дуже простою, бо Цитовича створені таблиці для отримання корегуючого коеф. К при певних питомих навантаженнях, глибинні точки, відстані від почки до перерізу по якому діє сила.

14. Дія місцевого рівномірно розподіленого навантаження у випадку просторової задачі.

Вирішенні просторової задачі при рівномірно розподіленому навантаженні отримане для прямокутної ділянки завантаження, деформації якої відповідають деформаціям поверхні лінійно деформованого напівпростору, тобто для умов вельми гнучкого передавання навантаження. При вирішенні задачі використовують метод кутових точок, запропонований Цитовичем. Метод використовують для визначення величин стискаючих напружень в різних точках простору ґрунтової основи у тому випадку, коли завантажена площина може бути розділена на прямокутники так, щоб дослідна точка стала кутовою. Тоді величина стискаючого напруження в цій точці буде дорівнювати алгебраїчній сумі напружень від прямокутних площин завантаження, для яких ця точка є кутовою.

15. Визначення стискаючих напружень за методом кутових точок.

Метод кутових точок для визначення величин стискаючих напружень в різних точках простору ґрунтової основи під дією рівномірно розподіленого навантаження застосовують в тому випадку, коли завантажена площина може бути розділена на прямокутники так, щоб дослідна точка стала кутовою. Тоді величина стискаючого напруження в цій точці (для горизонтальних рівнів, паралельних плоскій межі грунтового простору) буде дорівнювати алгебраїчній сумі напружень від прямокутних площин завантаження, для яких ця точка є кутовою.

В розрахунках стискаючих напружень для будь-якої точки простору ґрунтової основи використовуються кутові коефіцієнти _о та _с .Під центром завантаженого прямокутника максимальне стискаюче напруження розраховується за формулою: ;

а для точок під кутом завантаженого прямокутника: ;

де: та 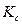- коефіцієнти з таблиці; - інтенсивність рівномірно розподіленого навантаження.Значення коефіцієнтів залежать від відносної глибини або та співвідношення сторін прямокутної площини завантаження ;

; ;

; ;

Користуючись цими залежностями, по таблиці можна визначити коефіцієнти як для центральної , так і для кутових точок .

Якщо точка розташована в центрі прямокутника зовнішнього навантаження,

то величина визначається за формулою: ; Точка розташована на межі прямокутника зовнішнього навантаження,то величина визначається як сума двох кутових напружень відповідних прямокутників навантажень:

; Точка розташована в межах прямокутника зовнішнього навантаження,то величина визначається як сума кутових напружень чотирьох прямокутників завантаження (в межах основного прямокутника . Точка знаходиться за межами прямокутника зовнішнього навантаження, величина визначається як алгебраїчна сума кутових напружень чотирьох прямокутників завантаження (в тому числі ): .

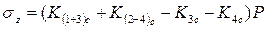В певних межах для ґрунтів прийнятною є лінійна залежність між напруженнями та деформаціями. Проте, для визначення загальних деформацій (пружних та залишкових: ущільнення, пластичної течії, повзучості тощо) необхідно враховувати додаткові умови, які враховують фізичну природу ґрунтів, як дисперсних тіл, а саме їх стискання, водопроникнення, контактний опір здвигання, структурно-фазові деформації.

16.Розподіл напружень у випадку плоскої задачі. Ізобари,розпори,здвиги.

Розподіл напружень у випадку плоскої задачі.Умови плоскої задачі мають місце у випадках, коли напруження розподіляється у одній площині, а напрямку перпендикулярному вони або рівні нулю, або постійні. Ця умова має місце для дуже витягнутих споруд (стрічкових фундаментів, основ підпірних стінок тощо). Використовуючи формули для визначення напружень в лінійно деформованому масиві від погонного навантаження (Фламана) в умовах плоскої задачі шляхом інтегрування напружень від дії елементарних сил. Отримують вирази для складових напружень для різних видів розподілених навантажень: рівномірної, зростаючої по закону прямої тощо.

Схема дії рівномірно розподіленого навантаження в умовах плоскої задачі

показана на рис. 7

Рис.7. Розрахункові схеми для визначення напружень при дії рівномірно розподіленого навантаження в умовах плоскої задачі. Ізобари, розпори, здвиги.

Для складових напружень будуть справедливі вирази:

Значення коефіцієнтів впливу знаходяться в таблиці відносно координат (z/b;y/b). Користуючись даними таблиць, можна легко побудувати епюри розподілу напружень по вертикальним та горизонтальним перерізам:А також лінії однакових стискаючих напружень (ізобари), лінії однакових горизонтальних напружень (розпори) та лінії однакових дотичних напружень (здвиги), які наочно характеризують напружену зону грунтової основи під смужкоподібним навантаженням. При визначенні напружень в ґрунтовій товщі під дією нерівномірного навантаження важливим складовим елементом є трикутне навантаження, тобто навантаження, інтенсивність якого змінюється за законом трикутника. Ізобари-ізолінії стискаючих напружень. Розпори-ізолінії горизонтальних напружень. Здвиги- ізолінії у тангенціальних напруженнях.

17.Дія рівномірно розподіленого навантаження у випадку плоскої задачі.

Умови плоскої задачі матимуть місце у випадках, коли напруження розподіляються головним чином в одній площині, в напрямку перпендикулярному їй вони постійні, або рівні нулю. Такі умови характерні для витягнутих у плані споруд, наприклад стрічкових та стінових фундаментів, основ підпірних стінок, гребель та подібних споруд.

Стискаючі напруження розраховуються за формулою:

,

де: 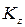- коефіцієнт впливу, значення якого залежить від величини відносних координат по вертикалі та по горизонталі , тобто . Значення коефіцієнта 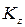можна взяти з таблиці, складеної М.О.Цитовичем.

18. Дія трикутного навантаження у випадку плоскої задачі.

При визначенні напружень в ґрунтовій товщі під дією нерівномірного навантаження важливим складовим елементом є трикутне навантаження, тобто навантаження, інтенсивність якого змінюється за законом трикутника, можна виконати такими способами: а) за формулою: ; б) за формулою через тангенси кутів та ;в) за допомогою коефіцієнтів з таблиці, складеної М.О. Цитовичем. г) за номограмою Остерберга для визначення дії навантаження, що змінюється за законом прямої.

19. Дія навантаження, що змінюється за законом прямої у випадку плоскої задачі.

Умови плоскої задачі матимуть місце у випадках, коли напруження розподіляються головним чином в одній площині, в напрямку перпендикулярному їй вони постійні, або рівні нулю. Такі умови характерні для витягнутих у плані споруд, наприклад стрічкових та стінових фундаментів, основ підпірних стінок, гребель та подібних споруд.

Стискаючі напруження розраховуються за формулою:

,

де: 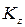- коефіцієнт впливу, значення якого залежить від величини відносних координат по вертикалі та по горизонталі , тобто . Значення коефіцієнта 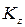можна взяти з таблиці, складеної М.О.Цитовичем для визначення напружень в дослідних точках, розташованих на показових вертикальних перерізах ( 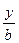= 0; 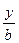= 0,25; 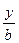= 0,5; 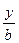= 1,0; 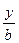=1,5; 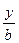=2,0) та горизонтальних інтервалах ( 0;0,25; 0,5; 0,75; 1,0; 1,5; 2,0; 3,0; 4,0; 5,0; 6,0), вибраних для зручності виконання розрахунків по координатних вісях та відповідно до ширини фундаменту .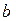

20. Розподіл напруження від власної ваги грунтової товщі.

Якщо грунтова товща складена неоднорідними грунтами, потрібно поділити його на інженерно-геологічні елементи і виконати розрахунок вертикальних та горизонтальних напружень на підошві і покрівлі кожного елементу. За даними напружень будують епюри, які мають ламаний характер. Спостерігається тенденція до зростання величин стискаючих напружень від власної ваги, оскільки певний шар грунту є при вантажений шарами ґрунтів, що залягають вище. Епюра горизонтальних напружень має фрагментальний характер, тому що кожний ІГЕ має свій коефіцієнт бічного тиску, який залежить від коефіцієнту Пуассона. За наявності води необхідно врахувати гідростатичний тиск, величини напружень у цих межах зменшаться, проте, на покрівлі водотриву спостерігається сходинка(на епюрі), яка утворюється за рахунок дії води як у вертикальному так і горизонтальному напрямку.

21. Загальна залежність між деформаціями і напруженнями у грунтовій товщі.

В певних межах для ґрунтів прийнятною є лінійна залежність між напруженнями та деформаціями. Проте, для визначення загальних деформацій (пружних та залишкових: ущільнення, пластичної течії, повзучості тощо) необхідновраховувати додаткові умови, які враховують фізичну природу ґрунтів, якдисперсних тіл, а саме їх стискання, водопроникнення, контактний опір здвигання,структурно-фазові деформації.

22. Принцип лінійної реформованості.

В певних межах для ґрунтів прийнятною є лінійна залежність між напруженнями та деформаціями. Проте, для визначення загальних деформацій (пружних та залишкових: ущільнення, пластичної течії, повзучості тощо) необхідно враховувати додаткові умови, які враховують фізичну природу ґрунтів, як дисперсних тіл, а саме їх стискання, водопроникнення, контактний опір здвигання, структурно-фазові деформації. Грунт являє собою неоднорідну масу. До певної величини навантаження буде спостерігатися лінійна деформація. В основному вона спостерігається до першої фази.існує такий момент або стан, коли після припинення дії сили вони повертаються в початковий стан. У таких умовах діє принцип лінійної деформофаності.

23. Теорія граничного напруженного стану

При подальшому збільшенні навантаження наступає друга фаза - фаза здвигів,

що переходить (в залежності від граничних умов і величини навантаження) у пластичну або прогресуючу течію, випирання, осідання та інші недопустимі деформації ґрунтових основ будівель. Залежність між деформаціями та напруженнями в цій фазі є нелінійною. На межі першої і другої фаз безпосередньо під штампом починає формуватися жорстке ядро обмежених зміщень часток ґрунту, яке в подальшому розтискає грунт в сторони. Поверхні ковзання.

У другій фазі при досягненні граничної несучої здатності ґрунту в залежності

від глибини закладання фундаментів та щільності ґрунтів можна виділити кілька

основних випадків з характерними поверхнями ковзання (див. рис.):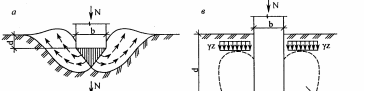

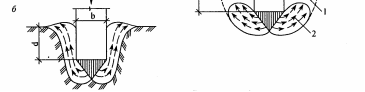
Рис. Випадки поверхонь ковзання при досягненні граничної несучої здатності ґрунту в залежності від глибини закладання фундаментів та щільності ґрунтів.

а) Фундаменти неглибокого закладання (h/b<1/2),для яких при граничному навантаженні характерне випирання ґрунту;

б) Фундаменти середньої глибини закладання (h/b=1/2-2), для яких при граничному навантаженні також спостерігається випирання, але оконтурюючи крива поверхонь сковзання має S - подібні обриси;

в) Фундаменти глибокого закладання (h/b=2-4), для яких при досяганні граничного навантаження випирання не спостерігається, але зона граничних здвигів досягає площини підошви фундаменту, деформуючи масив ґрунту, що розташований біля бічних стінок фундаменту.

Дата добавления: 2015-05-08