
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Стационарностью, «отсутствием последействия» и ординарностью
|
|
|
|
Свойство стационарности состоит в том, что вероятность появления k событий в любом промежутке времени зависит только от числа k и от длительности t промежутка времени и не зависит от начала его отсчета. Другими словами, вероятность появления k событий за промежуток времени длительностью t есть функция, за висящая только от k и t.
Свойство "отсутствия последействия" состоит в том, что вероятность появления k событий в любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка. Другими словами, предыстория потока не влияет на вероятности появления событий в ближайшем будущем.
Свойство ординарности состоит в том, что появление двух или более событий за малый промежуток времени практически невозможно. Другими словами, вероятность появления более одного со бытия за малый промежуток времени пренебрежимо мала по сравнению с вероятностью появления только одного события.
Интенсивностью потока X называют среднее число событий, которые появляются в единицу времени. Если постоянная интенсивность потока % известна, то вероятность появления k событий простейшего потока за время t определяется формулой Пуассона

19 билет
Интегральная теорема Лапласа. Имеет место следующее утверждение.
Теорема. Пусть производится n независимых опытов, в каждом из которых вероятность наступления события А одна и та же и равна 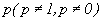 . Пусть m - число появления события A в n опытах. Тогда для достаточно больших n случайная величина m имеет распределение, близкое к нормальному с параметрами a=M(m)=np,
. Пусть m - число появления события A в n опытах. Тогда для достаточно больших n случайная величина m имеет распределение, близкое к нормальному с параметрами a=M(m)=np, 
20 билет
Однородный поток[править | править вики-текст]
Основная статья: Поток однородных событий
Поток заявок однороден, если:
· все заявки равноправны,
· рассматриваются только моменты времени поступления заявок, т.е. факты заявок без уточнения деталей каждой конкретной заявки.
Поток без последействия[править | править вики-текст]
Поток без последействия, если число событий любого интервала времени (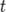 ,
,  ) не зависит от числа событий на любом другом непересекающемся с нашим (
) не зависит от числа событий на любом другом непересекающемся с нашим (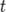 ,
,  ) интервале времени.
) интервале времени.
Стационарный поток[править | править вики-текст]
Поток заявок стационарен, если вероятность появления n событий на интервале времени (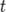 ,
,  ) не зависит от времени
) не зависит от времени 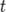 , а зависит только от длины
, а зависит только от длины  этого участка.
этого участка.
Простейший поток[править | править вики-текст]
Однородный стационарный поток без последействий является простейшим, потоком Пуассона.
Число  событий такого потока, выпадающих на интервал длины
событий такого потока, выпадающих на интервал длины  , распределено по Закону Пуассона:
, распределено по Закону Пуассона:
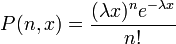
Пуассоновский поток заявок удобен при решении задач ТМО. Строго говоря, простейшие потоки редки на практике, однако многие моделируемые потоки допустимо рассматривать как простейшие.
21 билет
Случайная величина — это величина, которая принимает в результате опыта одно значение из множества исходов, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать.
Формальное математическое определение следующее: пусть  — вероятностное пространство, тогда случайной величиной называется функция
— вероятностное пространство, тогда случайной величиной называется функция  ,измеримая относительно
,измеримая относительно  и борелевской σ-алгебры на
и борелевской σ-алгебры на 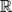 . Вероятностное поведение отдельной (независимой от других) случайной величины полностью описывается её распределением.
. Вероятностное поведение отдельной (независимой от других) случайной величины полностью описывается её распределением.
Случайные величины могут принимать дискретные, непрерывные и дискретно-непрерывные значения. Соответственно случайные величины классифицируют на дискретные, непрерывные и дискретно-непрерывные (смешанные).
На схеме испытаний может быть определена как отдельная случайная величина (одномерная/скалярная), так и целая система одномерных взаимосвязанных случайных величин (многомерная/векторная).
· Пример смешанной случайной величины — время ожидания при переходе через автомобильную дорогу в городе на нерегулируемом перекрёстке.
· В бесконечных схемах (дискретных или непрерывных) уже изначально элементарные исходы удобно описывать количественно. Например, номера градаций типов несчастных случаев при анализе ДТП; время безотказной работы прибора при контроле качества и т. п.
· Числовые значения, описывающие результаты опытов, могут характеризовать не обязательно отдельные элементарные исходы в схеме испытаний, но и соответствовать каким-то более сложным событиям.
С одной стороны, с одной схемой испытаний и с отдельными событиями в ней одновременно может быть связано сразу несколько числовых величин, которые требуется анализировать совместно.
· Например, координаты (абсцисса, ордината) какого-то разрыва снаряда при стрельбе по наземной цели; метрические размеры (длина, ширина и т. д.) детали при контроле качества; результаты медобследования (температура, давление, пульс и пр.) при диагностике больного; данные переписи населения (по возрасту, полу, достатку и пр.).
Поскольку значения числовых характеристик схем испытания соответствуют в схеме некоторым случайным событиям (с их определёнными вероятностями), то и сами эти значения являются случайными (с теми же вероятностями). Поэтому такие числовые характеристики и принято называть случайными величинами. При этом расклад вероятностей по значениям случайной величины называется законом распределения случайной величины.
22 билет
Случайная величина называется дискретной, если ее множество значений не более чем счетно, т.е. конечно или счётно.
Любое пространство элементарных событий не являющееся дискретным, называется недискретным, и при этом, если наблюдаемыми результатами (нельзя произносить случайными событиями) являются точки того или иного числового арифметического или координатного пространства, то пространство называется непрерывным (континуум). Пространство элементарных событий  вместе с алгеброй событий
вместе с алгеброй событий  и вероятностью
и вероятностью  образует тройку
образует тройку  , которая называетсявероятностным пространством.
, которая называетсявероятностным пространством.
Законы распределения дискретных случайных величин.
Так как дискретная случайная величина имеет конечное или счётное множество значений, то их можно просто перечислить и указать соответствующие вероятности. Это можно сделать, например, в форме таблицы
| X | x1 | x2 | ... | xn | ... |
| P | p1 | p2 | pn |
где,  - вероятность того, что X примет значение x
- вероятность того, что X примет значение x  .
.
Такую таблицу называют рядом распределения.
События  … несовместимы и в результате опыта одно из них обязательно происходит. Из этого следует
… несовместимы и в результате опыта одно из них обязательно происходит. Из этого следует

Для наглядности ряд распределения можно изобразить геометрически.
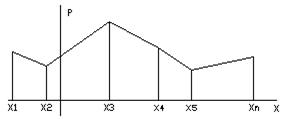
Для этого из каждой точки 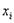 откладывают вверх отрезок равный
откладывают вверх отрезок равный 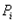 .На рисунке изображен многоугольник распределения.
.На рисунке изображен многоугольник распределения.
Примеры дискретных сл.вел: 1). Индикатор события I. Эта случайная величина имеет закон распределения: Если вероятность появления события в некотором опыте равна p, то I принимает значение 1, если событие произошло, и значение 0, если событие не произошло. I можно назвать числом появлений события в одном опыте.
| I | ||
| P | q | р |
2). Биномиальный закон распределения. Случайная величина может принимать значения 0,1,2,…,n и каждому значению X=m соответствует вероятность  , где p+q=1. Этот закон распределения считается заданным, если известны числа n и p, через которые выражаются все вероятности. Случайную величину подчинённою этому закону можно назвать числом появлении события в n независимых опытах.
, где p+q=1. Этот закон распределения считается заданным, если известны числа n и p, через которые выражаются все вероятности. Случайную величину подчинённою этому закону можно назвать числом появлении события в n независимых опытах.
З). Пуассоновский закон распределения. Случайная велbчина имеет возможные значения 0,1,2,3,…… и каждому значению Х=m соответствует вероятность  ,где
,где  - некоторый параметр, вероятностный смысл которого будет указан несколько страниц спустя.
- некоторый параметр, вероятностный смысл которого будет указан несколько страниц спустя.
4). Гипергеометрический закон распределения. Возможные значения X: 0,1,…,n. И каждому значению X=m соответствует вероятность P(X=m)=P  =
=  .
.  Эта случайная величина, например, равна числу m бракованных изделий среди n взятых наугад из партии объёма N, содержащей M бракованных изделий.
Эта случайная величина, например, равна числу m бракованных изделий среди n взятых наугад из партии объёма N, содержащей M бракованных изделий.
5). Геометрический закон распределения.
| X | … | n | … | |||
| P | p | qp | 
| … | 
| … |
q=1-p
Если, например, p – вероятность изготовления бракованной детали, то случайная величина X с этим законом распределения будет равна общему числу деталей до момента изготовления первой бракованной детали.
Построение ряда распределения удобно лишь для дискретных случайных величин, так как можно перечислить их все возможные значения.
23 билет
Распределения дискретных случайных величин
Биномиальное распределение. Дискретная случайная величина Х имеет биномиальное распределение, если ее возможные значения 0, 1, 2,..., m, …, n, а соответствующие им вероятности равны:
 (21)
(21)
где 0 < p < 1, q = 1 – p; m = 0, 1, 2,..., n.
Как видно из (21), вероятности Рm вычисляются, как члены разложения бинома Ньютона  , откуда и название «биномиальное распределение».
, откуда и название «биномиальное распределение».
Примером является выборочный контроль качества производственных изделий, при котором отбор изделий для пробы производится по схеме случайной повторной выборки, т.е. когда проверенные изделия возвращаются в исходную партию. Тогда количество нестандартных изделий среди отобранных есть случайная величина с биномиальным законом распределения вероятностей.
Биномиальное распределение определяется двумя параметрами: n и p. Cлучайная величина, распределенная по биномиальному закону, имеет следующие основные числовые характеристики:
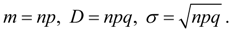 (22)
(22)
24 билет
Распределение Пуассона. Дискретная случайная величина Х имеет распределение Пуассона, если она имеет бесконечное счетное множество возможных значений 0, 1, 2,..., m, …, а соответствующие им вероятности определяются формулой:
 (23)
(23)
Примерами случайных явлений, подчиненных закону распределения Пуассона, являются: последовательность радиоактивного распада частиц, последовательность отказов при работе сложной компьютерной системы, поток заявок на телефонной станции и многие другие.
Закон распределения Пуассона (23) зависит от одного параметра а, который одновременно является и математическим ожиданием, и дисперсией случайной величины Х, распределенной по закону Пуассона. Таким образом, для распределения Пуассона имеют место следующие основные числовые характеристики:
25 билет
Геометри́ческое распределе́ние в теории вероятностей — распределение дискретной случайной величины равной количеству испытаний случайного эксперимента до наблюдения первого «успеха».Пусть X_1,\ldots, X_n,\ldots — бесконечная последовательность независимых случайных величин с распределением Бернулли, то есть
X_i = \left\{
\begin{matrix}
1, & p \\
0, & q \equiv 1-p
\end{matrix} \right.,\; i=1,2,\ldots
Построим случайную величину Y = \min \left\{ i \mid X_i = 1 \right\} - 1 — количество «неудач» до первого «успеха». Распределение случайной величины Y называется геометрическим с вероятностью «успеха» p, что обозначается следующим образом: Y \sim \mathrm{Geom}(p).
Функция вероятности случайной величины Y имеет вид:
\mathbb{P}(Y = n) = q^n p,\; n=0,1,2,\ldots
26 билет
| Пусть имеется конечная совокупность, состоящая из N элементов. Предположим, что D (defective) из них обладают нужным нам свойством. Оставшиеся N-D этим свойством не обладают. Случайным образом из общей совокупности выбирается группа из n элементов. Пусть Y - случайная величина, равная количеству выбранных элементов, обладающих нужным свойством. Тогда функция вероятности Y имеет вид: p_Y(k) \equiv \mathbb{P}(Y = k) = \frac{C_D^k\, C_{N-D}^{n-k}}{C_N^n}, где C_n^k \equiv \frac{n!}{k!\, (n-k)!} обозначает биномиальный коэффициент. Пишем: Y \sim \mathrm{HG}(D,N,n). | ||
| Гипергеометри́ческое распределе́ние в теории вероятностей моделирует количество удачных выборок без возвращения из конечной совокупности. |
27 вопрос
| Математи́ческое ожида́ние — среднее значение случайной величины (это распределение вероятностей случайной величины, рассматривается в теории вероятностей)[1]. В англоязычной литературе обозначается через \mathbb{E}[X][2] (например, от англ. Expected value или нем. Erwartungswert), в русской — M[X] (возможно, от англ. Mean value или нем. Mittelwert, а возможно от «Математическое ожидание»). В статистике часто используют обозначение \mu. | ||
| Следствие 10. Математическое ожидание существует тогда и только тогда, когда.Следствие 11. Если п.н., то.Следствие 12. Если п.н., но, то п.н.Следствие 13. Если п.н., то. |
28 вопрос
| ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ [ dispersion, variance of a discrete random variable ] Дисперсией дискретной случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D (X) = M (X - M (X)) 2. Для вычислений удобнее пользоваться формулой: D (X) = M (X 2) - (M (X)) 2. Дисперсия обладает следующими свойствами. 1. Дисперсия постоянной величины С равна нулю: D (C) = 0. 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D (CX) = C 2D (X). 3. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин: D (X+Y+Z) = D (X)+D (Y)+D (Z). 4. Дисперсия суммы постоянной величины и случайной - равна дисперсии случайной величины: D (C+X) = D (X). Дисперсию обозначают также как s 2 с нижним индексом, обозначающим соответствующую случайную величину или без него. | ||||
| Свойства дисперсии Дисперсия постоянной величины с равна нулю. Доказательство: по определению дисперсии [image] | 18:28:59 | |||
| При прибавлении к случайной величине Х неслучайной величины с ее дисперсия не меняется. D[X+c] = D[X]. Доказательство: по определению дисперсии [image] | ||||
| При умножении случайной величины Х на неслучайную величину с ее дисперсия умножается на с2. Доказательство: по определению дисперсии [image] | ||||
| Среднеквадрати́ческое отклоне́ние (синонимы: среднее квадрати́ческое отклоне́ние, среднеквадрати́чное отклоне́ние, квадрати́чное отклоне́ние; близкие термины: станда́ртное отклоне́ние, станда́ртный разбро́с) — в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания. При ограниченных массивах выборок значений вместо математического ожидания используется среднее арифметическое совокупности выборок. |
29 вопрос
| Непрерывные случайные величины. Кроме дискретных случайных величин, возможные значения которых образуют конечную или бесконечную последовательность чисел, не заполняющих сплошь никакого интервала, часто встречаются случайные величины, возможные значения которых образуют некоторый интервал. Примером такой случайной величины может служить отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе. Такого рода, случайные величины не могут быть заданы с помощью закона распределения вероятностей р(х). Однако их можно задать с помощью функции распределения вероятностей F(х). Эта функция определяется точно так же, как и в случае дискретной случайной величины: - See more at:http://www.toehelp.ru/theory/ter_ver/3_3/#sthash.5QA9.. | ||
| Законы распределения непрерывных случайных величин Закон распределения непрерывной случайной величины нельзя задать также, как для дискретной. Он неприменим в силу того, что нельзя перечислить все бесконечное несчетное множество значений, а вероятности каждого отдельно взятого значения непрерывной случайной величины равны нулю. Для описания закона распределения непрерывной случайной величины Х предлагается другой подход: рассматривать не вероятности событий Х=х для разных х, а вероятности события Х<х. При этом вероятность P(X<x) зависит от текущей переменной, т. е. является некоторой функцией от х. Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х:. Функцию F(x) называют интегральной функцией распределения или интегральным законом распределения. Способ задания непрерывной случайной величины с помощью функции распределения не является единственным. Необходимо определить некоторую функцию, отражающую вероятности попадания случайной точки в различные участки области возможных значений непрерывной случайной величины. Т. е. представить некоторую замену вероятностям pi для дискретной случайной величины в непрерывном случае. Такой функцией является плотность распределения вероятностей. Плотностью вероятности (плотностью распределения, дифференциальной функцией) случайной величины Х называется функция f(x), являющаяся первой производной интегральной функции распределения: |
30 вопрос
| Фу́нкция распределе́ния в теории вероятностей — функция, характеризующая распределение случайной величины или случайного вектора; вероятность того, что случайная величина X примет значение, меньшее или равное х, где х — произвольное действительное число. При соблюдении известных условий (см. ниже) полностью определяет случайную величину. | ||
| F_X непрерывна справа:[1] \lim\limits_{\varepsilon \to 0+} F_X(x+\varepsilon) = F_X(x) F_X не убывает на всей числовой прямой. \lim\limits_{x \to -\infty} F_X(x) = 0. \lim\limits_{x \to +\infty} F_X(x) = 1. Распределение случайной величины \mathbb{P}^X однозначно определяет функцию распределения. Верно и обратное: если функция F(x) удовлетворяет четырём перечисленным выше свойствам, то существует вероятностное пространство и определённая на нём случайная величина, такая что F(x) является её функцией распределения. По определению непрерывности справа, функция F_X имеет правый предел F_X(x+) в любой точке x\in \mathbb{R}, и он совпадает со значением функции F_X(x) в этой точке. В силу неубывания, функция F_X также имеет и левый предел F_X(x-) в любой точке x\in \mathbb{R}, который может не совпадать со значением функции. Таким образом, функция F_X либо непрерывна в точке, либо имеет в ней разрыв первого рода. |
| Плотность распределения Пусть имеется непрерывная случайная величина с функцией распределения, которую мы предположим непрерывной и дифференцируемой. Вычислим вероятность попадания этой случайной величины на участок от до: | ||||
| 1. Плотность распределения есть неотрицательная функция:. Это свойство непосредственно вытекает из того, что функция распределения есть неубывающая функция. 2. Интеграл в бесконечных пределах от плотности распределения равен единице:. Это следует из формулы (5.4.4) и из того, что. Геометрически основные свойства плотности распределения означают, что: 1) вся кривая распределения лежит не ниже оси абсцисс; 2) полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице. | ||||
| Как найти вероятность попадания случайной величины в заданный интервал? Это одна из самых известных и простейших задач теории вероятностей, которая в Wolfram|Alpha решается довольно просто. Вероятность попадания случайной величины X в числовой интервал (a; b) с помощью математической символики записывается следующим образом: Эта вероятность зависит от того, какое распределение вероятностей имеет данная случайная величина. Это важно понимать, и обязательно нужно учитывать при вычислениях. Вузовские пособия и курсы по высшей математике и теории вероятностей чаще всего подробно рассматривают вопрос о вычислении вероятности попадания в заданный интервал, лишь для нормально распределенной случайной величины, а также для дискретных случайных величин, которые имеют биномиальное распределение вероятностей. Потому-то о том, как искать вероятность попадания случайной величины X в заданный интервал, когда она имеет какое-либо иное распределение вероятностей, большинство студентов имеет лишь отдаленное представление. Однако же, в курсах математического моделирования, в технических, экономических дисциплинах возникает необходимость вновь обращаться к этой задаче. Причем, здесь нельзя ограничиться только лишь нормальным или биномиальным распределением вероятностей. Как найти вероятность попадания в заданный интервал для любой случайной величины? Ответ на этот вопрос также даст Wolfram|Alpha. Достаточно лишь ввести систему соответствующий запрос на вычисление вероятности. При этом нужно указать распределение случайной величины и параметры этого распределения |
|
|
|
|
|
Дата добавления: 2015-05-08; Просмотров: 1856; Нарушение авторских прав?; Мы поможем в написании вашей работы!