Оптимізація сітьових графіків

Оптимізація сітьових графіків здебільшого зводиться до скорочення тривалості критичного шляху та досягнення рівномірного завантаження виконавців на роботах.

Для скорочення тривалості критичного шляху слід проводити послідовне перетворення сітьового графіку за рахунок:

- скорочення тривалості робіт на критичному шляху через перерозподіл або залучення додаткових трудових ресурсів;

- зміни технологічного процесу виконання робіт, що знаходяться на критичному шляху.

Зазначені процеси продовжують доти, поки не буде одержано очікуваний результат, який задовольняв би як технологів, так і був економічно доцільним.

Для рівномірного розміщення виконавців упродовж всього терміну здійснення проекту необхідно реалізувати наступні кроки:

- перерозподіл працівників між роботами таким чином, щоб загальна кількість виконавців кожного періоду було однакова. Це, у свою чергу потребує зміни тривалості робіт, що може призвести до збільшення критичного шляху;

- переміщення початку здійснення роботи у межах резерву часу для цієї роботи.

Для оптимізації сітьового графіку необхідно побудувати лінійну діаграму у масштабі часу, де роботи розташовані за своїми ранніми початками. Дані для побудови такої діаграми можна взяти з таблиці розрахунку сітьового графіка чи графічного зображення, де числові значення внесено у відповідні сектори подій (див. рис. 24.1). Нумерація подій може починатися з 0 чи 1, що суттєвого значення немає. При великому комплексі робіт, зазвичай, окремі групи робіт і подій можуть виділятися і розраховуватися окремо. У цьому випадку вихідна подія може мати будь-який номер. У даному викладенні матеріалу умовно приймається нумерація вихідних подій з 1.

Отже, на лінійній діаграмі зображають роботу таким чином: кожна робота відображається відрізком (рис. 24.3). Початок цього відрізку встановлюється у координату із значенням на осі часу, яка відповідає ранньому початку роботи. Довжина відрізку – це тривалість самої роботи у періодах, що прийняті для конкретного проекту (години, дні, тижні). Кінці робіт позначаються номерами відповідних подій. Зазвичай, роботи, що знаходяться на критичному шляху, зображують потовщеною лінією.

Рис. 24.3. Побудова лінійної діаграми за сітьовою моделлю

Розпочинати побудову лінійної діаграми необхідно з роботи, яка виходить з початкової події та знаходиться на критичному шляху. На рис. 24.3 це − робота 1-2. Наступною будується інша робота критичного шляху – це робота 2-3. Таким чином, першим етапом є зображення на лінійному графіку усіх робіт критичного шляху (1-2, 2-3, 3-5).

Побудова робіт, що не належать до критичного шляху, провадиться наступним чином. Спочатку визначається час початку кожної роботи та її тривалість. Далі початок роботи зображується на діаграмі дещо вище кінця відрізку тієї роботи критичного шляху, до якої має відношення робота, що розглядається. На рис. 24.3 − це робота 1-3. Вона розпочинається, як робота 1-2, з події 1.

Під час побудови кожної роботи проставляється нумерація як початку так і кінця відповідно за номером подій, до яких відноситься дана робота. Над роботою у колі зазначається кількість працівників, що виконують дану роботу (окрім фіктивних робіт). Таким чином побудову лінійного графіку завершено.

Для оптимізації необхідно здійснити наступне. Підраховуємо кількість працюючих кожного періоду. Для підрахунку необхідно підсумувати кількість працівників кожної роботи на той чи інший період. Ці значення суми записуються для кожного періоду комплексу робіт (рис. 24.4).

Рис. 24.4. Графічний розрахунок кількості працюючих за періодами виконання комплексу робіт

Як видно з рис. 24.4, що кожного періоду різниться кількість працюючих від 9 до 1 чоловіка. Такий стан не може задовольняти керівництво. Для зміни ситуації проводиться оптимізація шляхом перерозподілу кількості працюючих на кожній роботі чи переміщення початку виконання робіт, для яких це можна реалізувати. З рис. 24.4 слідує, що є можливість скоротити роботу 3-5, збільшивши кількість виконавців. Проте, умовно будемо вважати, що зазначена робота не може бути скорочена за технологічними вимогами.

Критерієм оптимізації є найменше значення суми квадратів кількості працюючих на кожному періоді. Для випадку, що розглядається, сума квадратів становить:

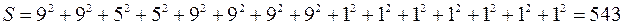
Розглядаємо ті роботи, що мають резерв часу. Цей резерв визначається таким чином. Якщо на лінійній діаграмі спостерігається певна розбіжність подій у часі для двох робіт, одна з яких – це робота, що знаходиться на критичному шляху, а інша – виходить з іншої події, то між закінченням однієї і початком наступної є певний проміжок у періодах. Ця робота може бути перенесена на декілька поділок шкали часу. На рис. 24.4 можливі варіанти перенесення роботи 4-5 зображені пунктиром.

Для розрахунку періодів переносу певної роботи використовується метод при якому розраховується оптимальне значення кількості періодів переносу робіт. Для реалізації цього методу будується таблиця з 4 стовпців та n рядків, де n – кількість періодів перенесення конкретної роботи. Так, за рис. 24.4 для роботи 4-5 необхідно 7 рядків. Перший стовпець заповняються числами, що відповідають кількості працівників кожного періоду, починаючи з першого дня, який слідує за закінченням роботи 4-5, і закінчуючи останнім значенням можливості переносу цієї роботи. Так, для роботи 4-5 цей період буде збігатися із закінченням роботи 3-5, що знаходиться на критичному шляху. Наступний стовпець формується з чисел, які відповідають кількості працюючих на відрізку від початку до кінця роботи, що розглядається (у нашому випадку − це робота 4-5) за винятком тих працівників, які безпосередньо зайняті на даній роботі (7 осіб). Для нашого прикладу, це буде 2 робітника тому, що загалом у ті періоди, під час яких виконується робота 4-5 ще здійснюється робота 2-3, на якій працює 2 чоловіка.

Третій стовпець формується як різниця між значеннями першого і другого числа кожного рядка. Четвертий стовпець будується наступним чином. Перше значення дорівнює числу першого рядка третього стовпця, наступні є сумою чисел, що знаходяться вище комірки та зліва від тієї комірки, що розраховується у даний час. Послідовність побудови і результат представлено на рис. 24.5.

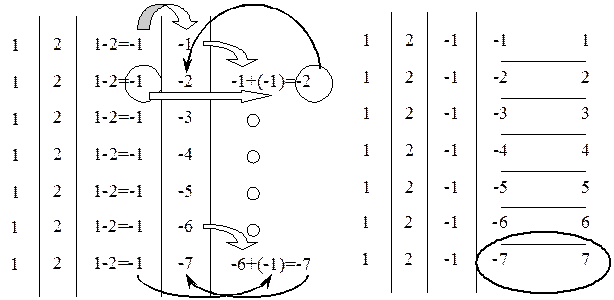
Рис. 24.5. Розрахунок кількості періодів перенесення роботи

За результатами табличного розрахунку визначаємо найменше число у четвертому стовпці. Для випадку, що розглядається, це число – 7. Для визначення кількості періодів для перенесення роботи 4-5 необхідно визначити, на який період припадає це мінімальне число. Для сітьової моделі, яка розглядається, це 7 період (див. рис. 24.4, 5 стовпець праворуч). Отже, для роботи 4-5 оптимальним є перенесення початку і кінця зазначеної роботи на 7 періодів. При перенесенні знову розраховуються відповідні значення чисельності працівників на кожному періоді. Рис. 24.4 трансформується у рис. 24.6.

Аналіз розподілу працюючих за періодами дозволяє дійти висновку, що необхідна кількість виконавців зменшилася, а саме до оптимізації нагально було розподіляти по роботам 9 осіб на 6 днів, після оптимізації тільки на 2 дні необхідно залучити 9 осіб. Частково зникла незначна кількість працюючих упродовж значних відтинків часу.

Рис. 24.6. Частково оптимізована лінійна діаграма

Так, до оптимізації по 1 робітнику працювало 7 днів, після проведення оптимізації – тільки 3 дні. За критерієм оптимізації маємо:

Це значення менше, ніж попереднє (543 < 487).

Досліджуючи оптимізовану за першим етапом лінійну діаграму, можна помітити, що з’явилася можливість оптимізувати роботи 2-5 чи 1-3. Після оптимізаційних процедур і для зазначених робіт варто знову проаналізувати діаграму на можливість оптимізації.

Окрім оптимізації методом переносу робіт, використовується розподіл чи перерозподіл кількості працюючих по роботах. Так, якщо робота при проектуванні сітьової моделі потребує N працюючих при часу виконання T періодів, то можна розглянути можливість виконання цієї роботи за 2 T при чисельності виконавців N /2. Звичайно, такий перерозподіл може виконуватися тільки при технологічних можливостях, враховуючи ресурсний потенціал та інші фактори. Як альтернатива вищезазначеному, можливо й інший розподіл за часом і кількістю, наприклад, 2 N і T /2, N /3 і 3 T, або інші варіанти.

Розглянемо оптимізацію методом перерозподілу працівників для сітьової моделі (див. рис. 24.4). Для скорочення чисельності працюючих є можливості для робіт, що не лежать на критичному шляху, зменшити кількість працівників. Так, для роботи 1-3, яку виконують 4 працівника, пропонується скоротити їх до 2 і збільшити термін виконання у 2 рази. Для роботи 2-4 залишити одного працівника і подовжити виконання у 3 рази. Виконання роботи 4-5 збільшити за часом у 2 рази з кількістю виконавців - 4. Таким чином, лінійна діаграма має вигляд, представлений на рис. 24.7 з наступним розрахунком кількості працюючих на кожному періоді.

Рис. 24.7. Графічний розрахунок кількості працюючих за періодами виконання комплексу робіт

Аналіз чисельності працюючих на кожному періоді дозволяє зробити висновок, що різниця між максимальною чисельністю (9 осіб) протягом 6 періодів і мінімальною (1 особа) зменшилася до 7 осіб упродовж 5 періодів і 1 особа протягом 3 періодів. Рівномірність розподілу суттєво покращилася.

За критерієм оптимізації маємо:

Це значення менше ніж попереднє (445 < 487 < 543).

Аналізуючи графічне зображення лінійної діаграми, можна дійти висновку, що є ще можливість скорочення часу виконання всього комплексу робіт. Так, змінюючи технологію (при можливості) і збільшуючи кількість виконавців на роботі 3-5, яка належить до критичного шляху з однієї особи до двох можливе скорочення часу реалізації цієї роботи у 2 рази (у нашому випадку на 3 періоди, до завершення роботи 4‑5). Такий перерозподіл працівників за періодами виконання робіт надає можливість поступово досягти оптимальної завантаженості працюючих і мінімізації часу виконання усього комплексу робіт.

У зв'язку з тим, що кожна операція зміни кількості періодів і кількості працюючих трансформує сітьовий графік, виникає необхідність переглядання його структури, адже можлива зміна робіт, що лежать на критичному шляху. Кожного перерозподілу робітників змінюється рівномірність працюючих за періодами. У зв'язку з цим виникає необхідність перенесення початків і закінчень робіт для вирівнювання працюючих протягом усього комплексу робіт і навпаки, положення кожної роботи, у свою чергу, дає можливість зміни часу виконання роботи. Графік удосконалюється. Закінченням процесу удосконалення можна вважати такий розподіл робіт і працівників на кожній роботі, який задовольняє усі служби, залучені до виконання комплексу робіт.

Проте ідеальна модель сітьового графіку з точки зору часу виконання комплексу робіт, завантаженості виконавців може не задовольнити вимоги технологічного процесу. При проектуванні та оптимізації сітьових моделей варто враховувати наступні чинники:

- період, який використовується у розрахунках сітьових графіків необхідно брати такий, який є кратним і доцільним для усіх робіт, що входять до комплексу;

- розраховуючи необхідну кількість працівників на кожній роботі, належним чином треба аналізувати особливості цієї роботи;

- склад персоналу за професіями і рівнем кваліфікації на кожній роботі має відповідати рівню складності й трудомісткості цієї роботи;

- при перерозподілі робітників між різними роботами враховується їх кваліфікаційний рівень, професія та необхідність такого переміщення;

- зміна часу виконання робіт має обґрунтовуватися з точки зору технологічної можливості та наявних людських і матеріальних ресурсів, кадрового потенціалу;

- зменшення часу виконання окремих робіт може бути неможливе у зв'язку з тим, що конкретна робота містить природні процеси у своєму складі, які проходять за певний проміжок часу (сушіння фарби, полімеризація, термопрогонка);

- кількість часу, яку варто заощадити, включаючи у роботу кожного додаткового працівника, може нелінійно залежати від їх кількості, і навпаки, вилучення виконавця також нелінійно впливатиме на збільшення часу виконання роботи;

- в окремих випадках вилучення виконавця зменшує час виконання роботи, а залучення додаткового може збільшити цей час;

- специфічні роботи можуть виконуватися тільки певними професіоналами чи групами працівників (відділи, бригади), перерозподіл може бути не доцільним чи неможливим;

- оптимізуючи час виконання і кількість працюючих, необхідно пам’ятати, що будь-який зовнішній чи внутрішній фактор може суттєво вплинути як на час (доставка матеріалів із запізненням, непередбачені затримки у роботі), так і на зміну кількості працівників (хвороба, перехід на іншу роботу), отже варто для кожної роботи мати резерви часу і трудових ресурсів.

Підсумовуючи вищезазначене, варто відмітити, що побудова і оптимізація сітьових графіків є трудомістким процесом, на який впливає певна кількість факторів. Сам процес реалізації проекту, який розрахований методом сітьового планування, потребує постійного перегляду строків і виконавців й під час виконання.

Контрольні питання

1. Назвіть основні завдання планування інноваційних процесів.

2. Дайте визначення поняття “сітьова модель”, “сітьовий графік”, “сітьове планування”.

3. Опишіть основні типи сітьових моделей.

4. Наведіть назву основних і специфічних елементів сітьової моделі.

5. Дайте визначення критичного шляху для сітьової моделі.

6. Наведіть основні правила побудови сітьової моделі.

7. Зазначте різницю між детермінованими та імовірнісними оцінками тривалості часу виконання роботи.

8. Наведіть послідовність розрахунку сітьової моделі.

9. Назвіть основні методи оптимізації сітьових графіків.

10. Вкажіть на чинники, що необхідно враховувати при проектуванні та оптимізації сітьових моделей.

Завдання з розв’язанням

Побудуйте, розрахуйте та оптимізуйте (за кількістю виконавців та за тривалістю критичного шляху) сітьову модель виготовлення приладу. Для реалізації проекту необхідно виконати 7 робіт. Склад роботи, залежності, кількість виконавців та час виконання представлені у табл. 24.2.

Таблиця 24.2. Вихідні дані для реалізації проекту

№ з/п	Склад роботи	Назва роботи	Кількість виконавців	Час виконання, дні
1.	Розробка технічного завдання	1-2
2.	Підготовка документації	1-3
3.	Набір і підготовка персоналу	2-3
4.	Виготовлення вузла А	2-4
5.	Комплектація вузла Б	3-4
6.	Складання	4-5
7.	Виготовлення упаковки	3-5

Розв'язання:

За даними табл. 24.2 визначаємо логічну залежність робіт і будуємо сітьовий графік (рис. 24.8).

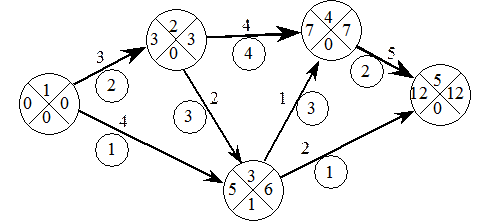
Рис. 24.8. Сітьова модель проекту виготовлення приладу

За аналізом графіка маємо критичний шлях за подіями 1-2-4-5, загальний час виконання проекту становить 12 днів. Для аналізу завантаженості працівників необхідно побудувати лінійну діаграму сітьової моделі (рис. 24.9) та розрахувати кількість виконавців, які виконують роботи кожного дня. Як видно з діаграми, кількість виконавців змінюється від 2 до 8, що не може повною мірою задовільнити керівництво.

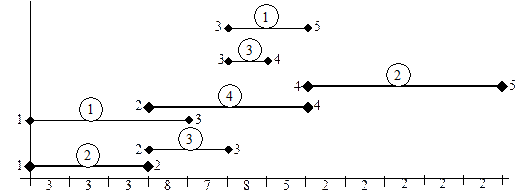
Рис. 24.9. Лінійна діаграма сітьової моделі виготовлення приладу

Одна із робіт (2-4), що лежить на критичному шляху може мати меншу тривалість. Адже збільшення кількості працюючих на виготовленні вузла А призведе до скорочення цієї роботи. У зв’язку з цим, пропонується розмістити на зазначеній роботі 5 виконавців. Припускаємо, що робота скоротиться на 1 робочий день і буде складати 3 дні. Зображаємо діаграму з врахуванням змін (рис. 24.10).

Рис. 24.10. Лінійна діаграма сітьової моделі при скороченні критичного шляху для роботи 2-4

У даному випадку кількість працюючих змінюється від 2 до 9, що погіршило рівномірність виконавців за періодами роботи, проте на 1 день зменшився термін виконання всього проекту. Для оптимізації перерозподілом робіт по днях побудуємо таблиці, у яких розрахуємо кількість днів переносу робіт, які мають резерви часу. Такими роботами є 1-3 та 3-5. Роботу 1-3 можна перенести тільки на 1 день, адже роботи 2-3 та 3-4 після зменшення тривалості роботи 2-4 вже є критичними. Як бачимо на рис. 24.10, перенесення роботи 1-3 суттєвого покращення не здійснить. При такому перенесені першого дня буде працювати 2 особи, а 5 дня не 8, а 9. При такому переносі може погіршитися наступне: при будь-якому збої у виконанні роботи 1-3 може зірватися кінцевий термін реалізації проекту, адже подія 3 під впливом різних факторів також може переміститися у часі. Розглянемо оптимізацію роботи 3-5. Її можна перемістити на 1, 2, 3 і 4 дні. Таблиця матиме наступний вигляд (див. табл. 24.3).

Таблиця 24.3. Розрахунок для роботи 3-5

		-6	-6
			-6
			-6
			-6

За аналізом таблиці робимо висновок, що є можливість переміщати роботу на 1, 2, 3 чи 4 дні (мінімальне від’ємне значення належить всім дням, що розглядаються для оптимізації). При різних від’ємних значеннях обрали б найменше. Припускаємо, що доцільно перемістити роботу 3-5 на 1 день (подвійна рамка). Результат перенесення представлено на рис. 24.11. Після цієї ітерації залишився тільки один день, коли залучено 9 робітників.

Рис. 24.11. Лінійна діаграма сітьової моделі при оптимізації роботи 3-5 методом перенесення

Нарешті, пропонується скоротити роботу 4-5 з 5 до 3 днів шляхом залучення додаткових виконавців. Таким чином, оптимізована лінійна діаграма сітьового графіку має такий вигляд, показаний на рис. 24.12.

Рис. 24.12. Оптимізована лінійна діаграма сітьової моделі виготовлення приладу

Завершальним етапом є побудова сітьової моделі з урахуванням змін оптимізації (рис. 24.13).

Отже, процеси оптимізації дали змогу більш рівномірно розподілити виконавців (зменшити відношення кількості працівників по днях з 4 разів до 3) та зменшити термін виконання проекту з 12 до 9 днів, що вважаємо за задовільний результат. Для покращення результату ще можна зменшити час виконання робіт 1-2 і 2-3. Проте такий зміст роботи, що знаходяться на роботах 1‑2 та 2‑3, звичайно, не може залежати від кількості виконавців на зазначених роботах за своєю специфікою. Побудова та оптимізація сітьової моделі завершена.

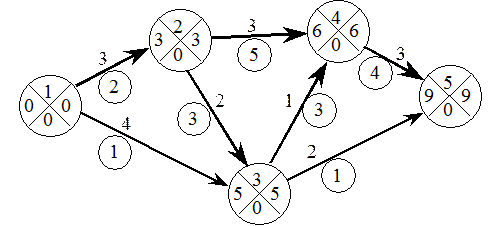
Рис. 24.13. Оптимізована сітьова модель проекту

Завдання для самостійного розв’язання

1. Побудуйте сітьовий графік за приведеними взаємозв’язками робіт. Роботи Е і Ж починаються після закінчення роботи А, робота Д – після закінчення робіт Б і Е. Робота Г – після закінчення робіт Б і Е. Робота Ж – після закінчення робіт Г, Д, З.

2. Розрахуйте основні параметри сітьової моделі, що зображена на рис. 24.14.

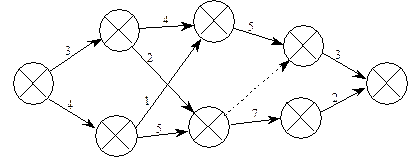
Рис. 24.14. Сітьова модель

3. Проведіть оптимізацію за приведеною лінійною діаграмою (рис. 24.15).

Рис. 24.15. Лінійна діаграма сітьової моделі

4. Виправте помилки у побудові сітьової моделі проекту А (рис. 24.16).

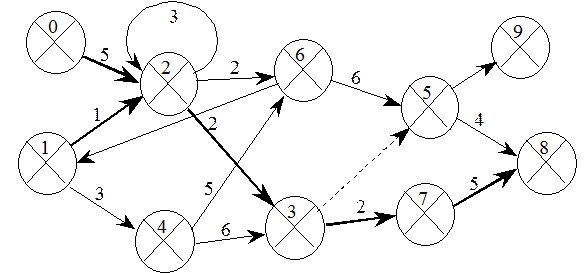
Рис. 24.16. Сітьова модель проекту А

5. Спростіть сітьовий графік проекту Б (рис. 24.17).

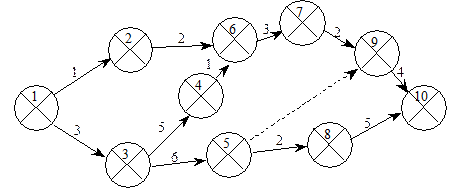
Рис. 24.17. Сітьова модель проекту Б

Глава 25

Дата добавления: 2015-05-23