Методи Ньютону

1.2.1. Загальна характеристика методів Ньютону

Методи Ньютону відносяться до методів другого порядку, тобто використовують другі частинні похідні цільової функції f (x). Всі вони є прямим узагальненням відомого методу Ньютону відшукання кореня рівняння:

φ (x)=0,

(3)

де φ (x) — скалярна функція скалярного аргументу x.

Метод Ньютону відшукання кореня рівняння описується наступною рекурентною формулою:

.

(4)

Цей метод ще називають методом дотичних для розв'язання рівняння (3).

Нехай тепер φ (x) — n -мірна вектор-функція векторного аргументу x тієї ж розмірності. Тоді для розв'язання системи рівнянь φ (x)=0 ми можемо використовувати ітераційний процес, аналогічний (4):

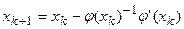
(5)

де 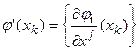— квадратна матриця n × n.

Розглянемо тепер випадок, коли вектор-функція φ (x) є градієнтом деякої скалярної функції f (x), тобто

φ (x)= f '(x).

Прирівнюючи її до нуля, приходимо до системи рівнянь, яка визначає координати стаціонарних точок функції f (x). Формула методу Ньютону для розв'язання цієї системи виглядає так:

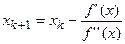
(6)

і отримується заміною в (6) φ (x_k) на f '(x).

Ітераційний процес (6) будує послідовність точок { x_k }, що при певних припущеннях сходиться до деякої стаціонарної точки x ^* функції f (x), тобто до точки, у якій f '(x ^*)=0. Якщо матриця других похідних f ''(x ^*) позитивно визначена, ця точка буде точкою локального мінімуму функції f (x).

Рис.. Узагальнена схема оптимізаційних методів Ньютону

Дата добавления: 2015-05-23