Метод Ньютону

У методі Ньютону послідовність точок спуску визначається формулою (6). Для поточної точки x_k напрямок і величина спуску визначається вектором 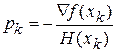. Хоч у визначенні вектору p_k фігурує обернена до H (x_k) матриця 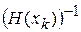, на практиці немає необхідності обчислювати останню, оскільки напрямок спуску p_k можливо знайти як розв’язок системи лінійних рівнянь

(7)

яким-небудь із методів.

Схема алгоритму методу Ньютону.

Крок 1.

На першій ітерації, при k =0, задаються:

x ₀ — початкове наближення;

ε — умова зупинки.

Обчислюються градієнт 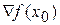і матриця .

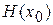Крок 2.

Визначається напрямок спуску p_k, як розв'язання системи лінійних рівнянь

(наприклад, методом виключення Гаусу).

Крок 3.

Визначається наступна точка спуску:

.

Крок 4.

Обчислюються в цій точці x_{k +1} градієнт f '(x_{k +1}) і матриця f ''(x_{k +1}).

~

Крок 5.

Якщо , то пошук на цьому закінчується й покладається

.

Інакше k = k +1 і перехід до кроку 2.

Особливістю методу Ньютону є те, що для квадратичної цільової функції він знаходить мінімум за один крок, незалежно від початкового наближення x ₀ і ступеня яружності.

У загальному випадку, коли функція, що мінімізується, не квадратична, вектор 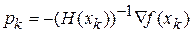не вказує в точку її мінімумі, однак має велику складову вздовж осі яру та значно ближче до напрямку на мінімум, ніж антиградієнт. Цим і пояснюється вища збіжність методу Ньютону в порівнянні з градієнтними методами при мінімізації яружних цільових функцій.

Недоліками методу Ньютону є те, що він, по-перше, вимагає обчислення других похідних і, по-друге, може розходитися, якщо початкове наближення перебуває занадто далеко від мінімуму.

Рис.

1. Алгоритм методу Ньютону для випадку n =2.

Дата добавления: 2015-05-23