Математическое моделирование (гидравлики ) механики жидкости в ПТС

Процессы движения жидких и газовых сред составляют одну из основ многих технологий в ПТС. Полная их классификация чрезвычайно объемна, но возможно выделение наиболее распространенных гидравлических процессов в ПТС. К таким относятся:

1. Гидравлические процессы, связанные с перемещением масс жидкости или газа по гидравлическим (газовым) сетям (трубопроводам, каналам и пр.). Моделирование этих процессов имеет основной своей целью – определение параметров нагнетателей и рабочих режимов трубопроводной сети, в более сложных задачах и определение оптимальных параметров сети, включая форму сети, диаметры трубопроводов и т. д. ит.п.

2. Процессы перемешивания жидких сред с целью создания равномерного распределения компонентов например в суспензиях (жидкость – твердые частицы) или в эмульсиях (жидкость + жидкость – эмульсия) или в пенах (жидкость + газ). И в этих проблемах одна из важнейших задач связана с определением рациональных параметров механизмов перемешивания.

3. Организация процессов разделения несущих сред и распределенных в них частиц, пузырьков, капель и т.д. и т.п. Возможна простейшая организация этих процессов, например – осаждением в поле тяжести, или применением электро – механических или центробежных сил различной формы. Как правило, в таких проблемах необходимо определение геометрии сосудов и параметров механических устройств решающим образом влияющих на процессы разделения.

4.Процессы фильтрования (частный случай процесса разделения). В модели определяются режимы и их параметры (время, геометрия, затраты энергии и др.).

5. Процессы организации псевдо – ожижения и кипящего слоя обычно выбираются для интенсификации тепло – массообмена в системах газ + твердые частицы, газ + жидкость, газ + жидкость + твердые частицы. В этих проблемах задачи моделирования связаны с определением режимных параметров процесса: соотношение объемов фаз и компонентов, создание необходимых уровней скоростей фаз и компонентов, обеспечение равномерных или квази – равномерных распределений фаз и компонентов и др.

6. Организация кавитационных процессов, как мощных средств интенсификации, например при организации гомогенизации на молекулярном уровне, повышении интенсивности массообменапри очистках поверхностей и проч.

7. Процессы массообмена в капиллярно – пористых структурах составляют основу для моделирования таких сложных процессов как экстрагирование, сушка и пр.

8. Процессы перемещения неньютоновских жидкостей могут быть основой многих технологий с теми материалами, которые по своим физическим свойствам не могут считаться «ньютоновскими». В этих случаях моделирование эти особенности должно учитывать. Такой учет скажется и на интегральных параметрах оборудования.

9. Нестационарные процессы гидродинамики проявляются в тех случаях, когда в времени меняются поля скоростей и ускорений.

10. Процессы гидравлики газо – жидкостных систем: движение пузырей и капель в несущей среде; течение жидких пленок; распыление жидкости в газ, истечение газа в жидкость и жидкости в газ; движение двухфазных потоков в каналах и прочее.

11. Процессы гидравлики аппаратов с зернистым (дисперсным) слоем.

12. Нестационарные и переходные процессы в гидравлических системах и многие др.

Гидродинамика (гидромеханика – гидравлика) техническая наука, в которой изучаются законы равновесия и движения жидкостей, а также закономерности взаимодействий между жидкостью и стенками сосудов и трубопроводов, в том числе при движении жидкостей.

Жидкостями называют физические тела, обладающие а) в отличии от твердых тел – текучестью, б) в отличии от газа – малой изменяемостью объема (не сжимаемостью).

Изучение физических явлений в потоках жидкостей и газов сводится к рассмотрению трех видов полей: векторного поля скоростей и ускорений и двух скалярных полей – температуры и концентрации. Механика жидкости в своей основе рассматривает такие фундаментальные понятия как «идеальная жидкость», т.е. жидкость, при движении которой не учитываются вязкие взаимодействия с поверхностями, окружающими жидкость при ее движении. Другое важное понятие – реальная (вязкая) жидкость. Количественно эффект влияния вязкости учитывается введением коэффициентов вязкости динамической [Па * с] и кинематической

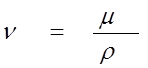[ ]. Понятие вязкость в гидродинамике используют для выделения двух

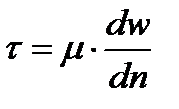разных ее типов. Отличают «ньютоновские» и «неньютоновские» жидкости. Для первых предполагается, что сила трения пропорциональна первой степени градиента скорости по нормали и элементарный закон этот описывается соотношением вида: 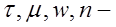где напряжения трения, коэффициент динамической вязкости, скорость и нормаль к ней.

Математические модели гидравлических сетей. Главной задачей расчета гидравлической сети как правило является определение параметров нагнетателя (насоса). Существующие типы сетей удобно разделять на магистральные и разветвленные. Важным моментом выбора нагнетателя является определение его мощности на прокачку теплоносителя. Эта задача решается с помощью известного простого уравнения: 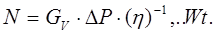Здесь:

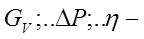массовый расход теплоносителя, потери напора в гидравлической сети, к.п.д. насоса, соответственно.

Для магистрального трубопровода, в котором диаметр канала не меняется по длине, а местные сопротивления отсутствуют для определения общих потерь давления можно использовать известную из гидравлики формулу:

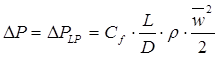В этой формуле коэффициент трения по длине,

который может быть найден в зависимости от режима течения по следующим формулам: 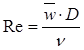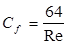для ламинарного режима течения и

для турбулентного режима. Для сложных, разветвленных трубопроводов, состоящих из системы последовательно соединенных участков, полные потери давления по длине могут определяться как суммы потерь по участкам:

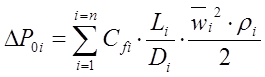Здесь: средняя скорость и номера отдельных линейных и местных сопротивлений, длины

их, площадь живого сечения, соответственно.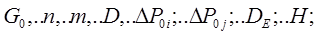

общий массовый расход теплоносителя в трубопроводе, общее число линейных участков и местных сопротивлений, диаметр трубы, полные потери давления по длинам и местным сопротивлениям, эквивалентный диаметр и периметр канала, соответственно. Определение эквивалентного диаметра всегда требуется, когда форма канала не является цилиндрической. Формула по которой это делается имеет следующий вид: 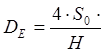В тех задачах, когда заданы располагаемые

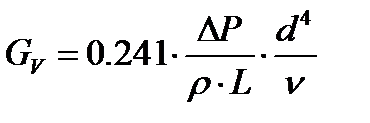потери давления, а объектом расчета является тот допустимый массовый, объемный расход теплоносителя, при котором эти потери не будут превзойдены. Для этих задач из соотношений для потерь давления получены необходимые расчетные формулы - для ламинарного режима: и для

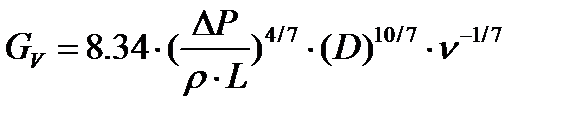турбулентного режима: это для объемного расхода.

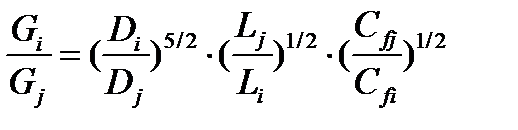Для расчета разветвленных трубопроводов существенными являются соотношения, определяющие распределения расходов и перепадов давления при параллельном и последовательном их соединении. При параллельном соединении важным является условие равенства потерь давления в параллельных ветвях. Это равенство потерь давления для условий ламинарного течения приводит к следующему соотношению массовых расходов:

Поскольку известно, что 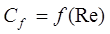и зависит от типа режима, то последующее решение не вызывает затруднений и при двух ветвях для турбулентного режима получим: 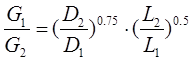и для ламинарного режима имеем: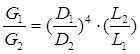

Если число параллельных ветвей больше двух, то схема решения не меняется. Она основывается на указанных основных положениях. Т.е. равенство потерь давления и регламентация суммарного расхода.

Выбор нагнетателя. По существу задача выбора нагнетателя сводится к поиску такого решения, когда требования работы трубопроводной системы должны обеспечиваться возможностями нагнетателя (насоса, если перекачивается жидкость). Для трубопроводной системы рабочая характеристика – это зависимость потерь давления от массового расхода. Эта зависимость имеет вид:

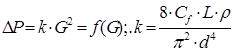Зависимость же массового расхода от создаваемого

напора для такого нагнетателя как центробежный насос имеет другую форму:

Ниже на графиках показаны различные типичные варианты решения проблемы определения условий совместной работы сети и центробежного насоса. В практике распространены два основных приема управления режимами совместной работы насоса и сети: 1.Когда в характеристику насоса вводится некоторый запас по его напору при сохранении требований о максимально возможном массовом расходе.

2. Когда в отличие от предыдущего варианта такой запас не вводится.

Этим двум вариантам управления согласованием характеристик насоса и сети отвечают два способа их технологической реализации: 1. В первом случае при наличии запаса по напору насоса, в гидравлической схеме насос + сеть вставляют задвижку, позволяющую за счет введения дополнительного гидравлического сопротивления получить нужный массовый расход; 2. В втором случае используют возможности тиристорного управления числом оборотов электродвигателя и за счет этого добиваются полного согласования параметров насоса и сети. Соответствующие этим двум приемам гидравлические схемы показаны ниже:

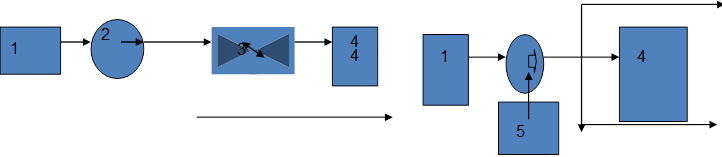
Схемы гидравлической разводки. а) Схема регулирования расхода с помощью задвижки; б) Схема регулирования расхода с помощью частотного преобразователя. 1 – Источник жидкости; 2 – насос; 3 – задвижка; 4 – технологический аппарат; 5 – частотный преобразователь.

Ниже представлены типичные графики зависимостей напора и потерь давления от расхода для сети и центробежного насоса и условия их согласования.

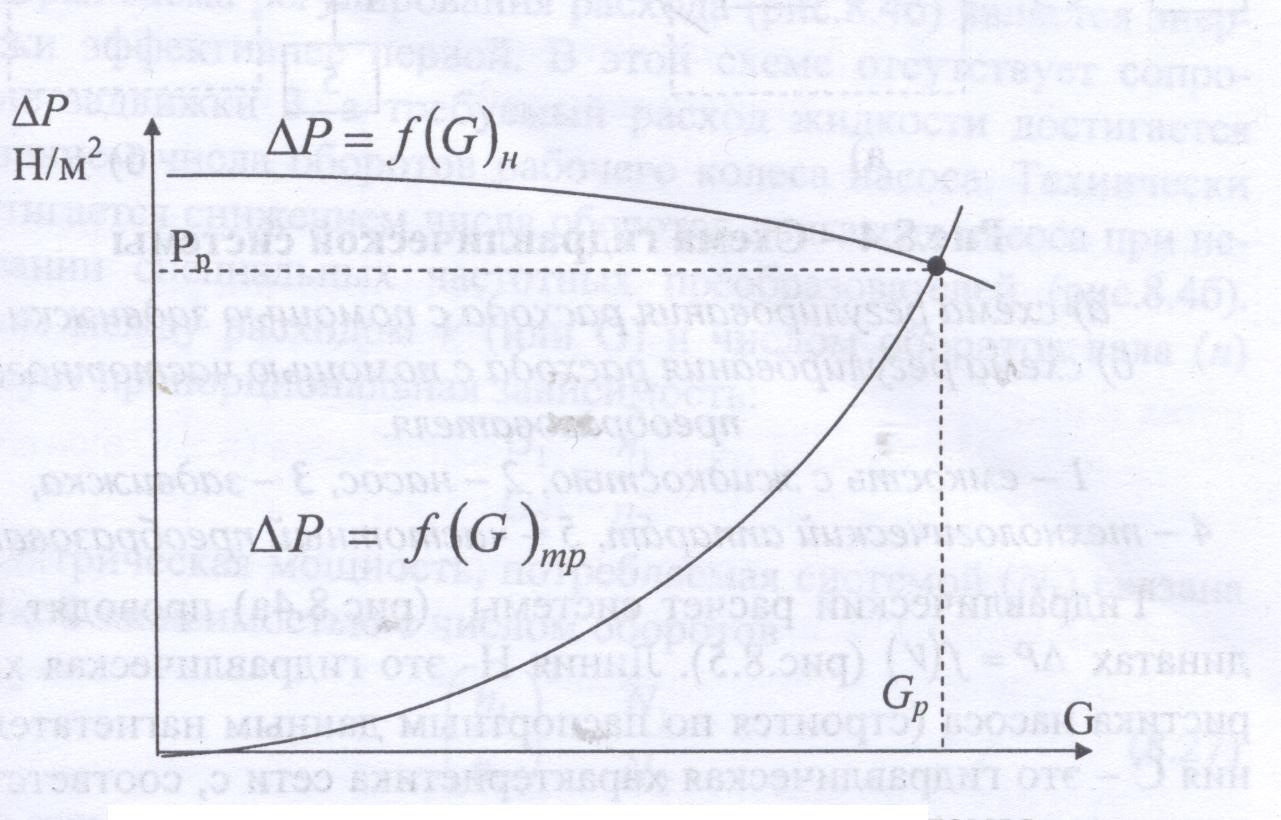
Типичная форма согласования рабочих параметров сети и центробежного насоса

Математическое моделирование (гидравлики) механики жидкости в ПТС

Ниже на графике показана типичная форма согласования параметров совместной работы насоса и трубопроводной сети. РТ – рабочая точка; н – характеристика насоса; с – характеристика сети. V1, V2, Vp – объемные расходы для различных характеристик сети и данной характеристики насоса.

= гидравлические характеристики насоса и сети, соответственно

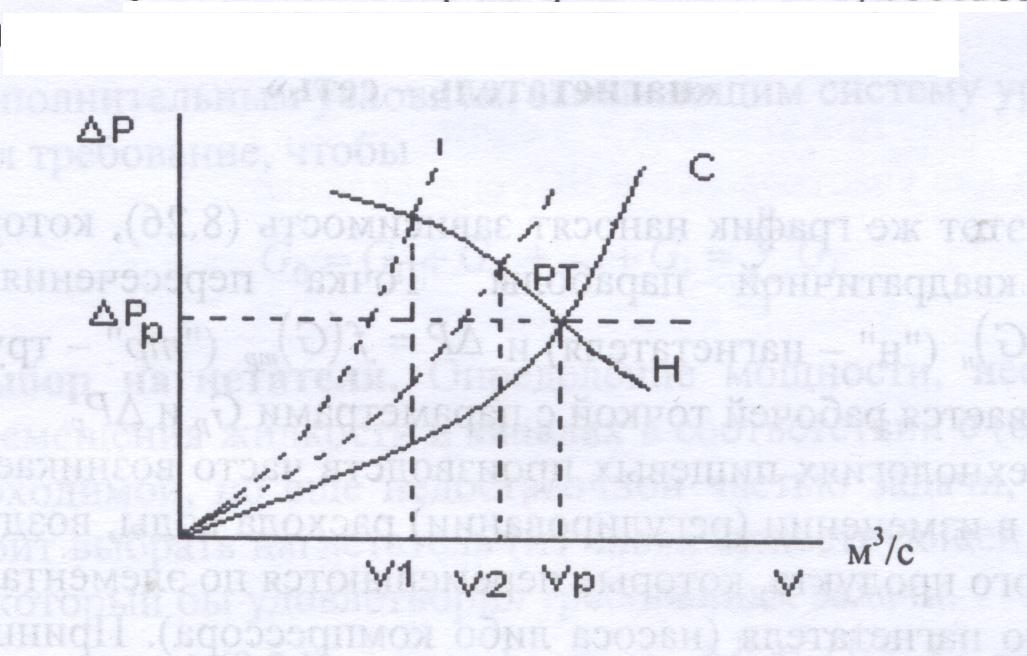
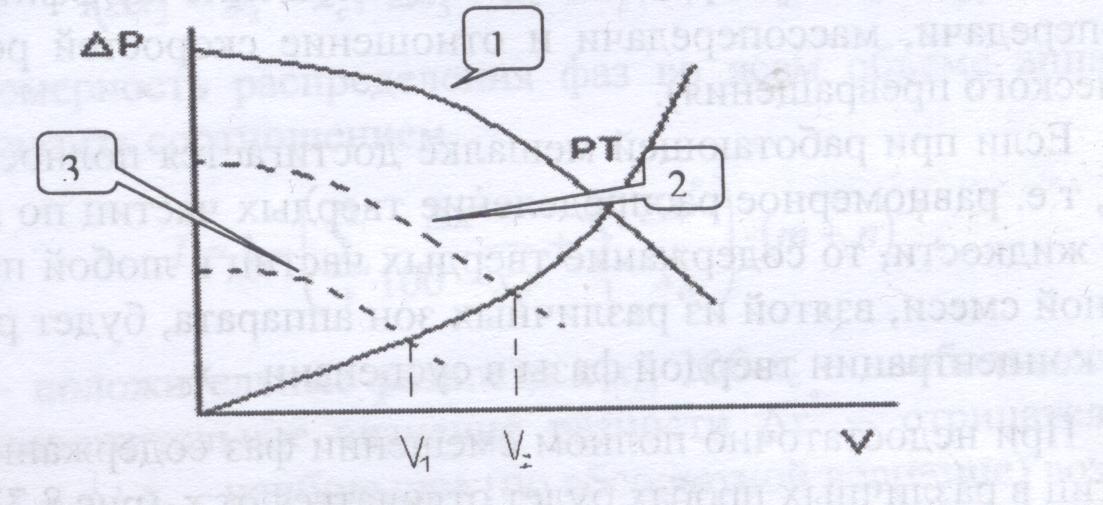
Выше приведены рисунки в графической форме, показывающие реализацию процедуры согласования (решения) характеристик насоса и сети (в общем виде) и при разных рабочих характеристиках сети. Ниже в такой же форме представляются различные формы этого согласования при другой схеме управления работой насоса. Когда осуществляется тиристорное управление числом оборотов центробежного насоса. Ниже линия 1 – рабочая линия насоса при номинальном режиме. Линии 2 и 3 при более низких числах оборотов двигателя насоса. Соответственно, видно снижение перекачиваемых объемов теплоносителя.

Перемешивание является широко распространенным и весьма важным процессом пищевых технологий. Типичные целями этого процесса являются:

- создание однородных растворов, суспензий, эмульсий;

- интенсификация процессов теплообмена в аппаратах, физических и химических реакторах и др.

- интенсификация процессов массообмена (включаяих сочетание с химическими и биохимическими реакциями).

Интенсивность перемешивания определяется количеством энергии, вводимой в единицу объема Эффективность перемешивания является важной характеристикой качества процесса. Если при работающем устройстве перемешивания достигается полное смешение фаз в аппарате, т. е. равномерное их распределение по всему объему жидкости, то содержание частиц разных фаз в любой пробе полученной смеси, взятой из разных зон аппарата должно быть равным средней концентрации их в всем аппарате. При недостаточном качестве перемешивание содержание перемешиваемых частиц в различных пробах будет составлять некое распределение. Количественно равномерность распределения частиц (фаз) по всему объему можно выразить следующим соотношением:

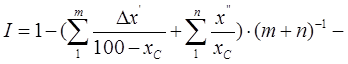здесь: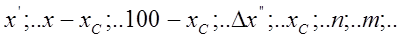

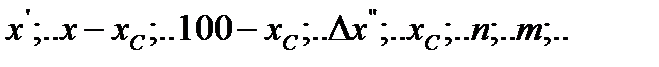
- положительные разности 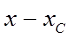; наибольшее возможное положительное

значение разности 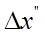; отрицательные разности 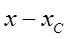наибольшее возможное

(по абсолютной величине) возможное отрицательное значение разности 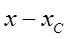; n – число проб, в которых разность 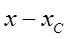отрицательна.

Для количественной характеристики процесса перемешивания используют также методы теории подобия и модифицированные числа Эйлера и Рейнольдса. Здесь определяющая скоростьвычисляется по формуле: 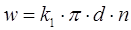число Рейнольдса определяется так: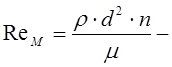

В выражении для числа Эйлера величину потерь давления определяют исходя из следующих соображений. Предполагая известными затраты мощности N на

процесс перемешивания при известном объемном расходе перемешиваемой жидкости Q, получают для потерь давления при перемешивании следующую связь: 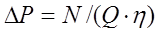здесь к.п.д. насоса. Тогда для числа Эйлера в процессе перемешивания получаем следующее выражение:

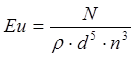Для разных типов мешалок существуют свои характеристики. Вот они.

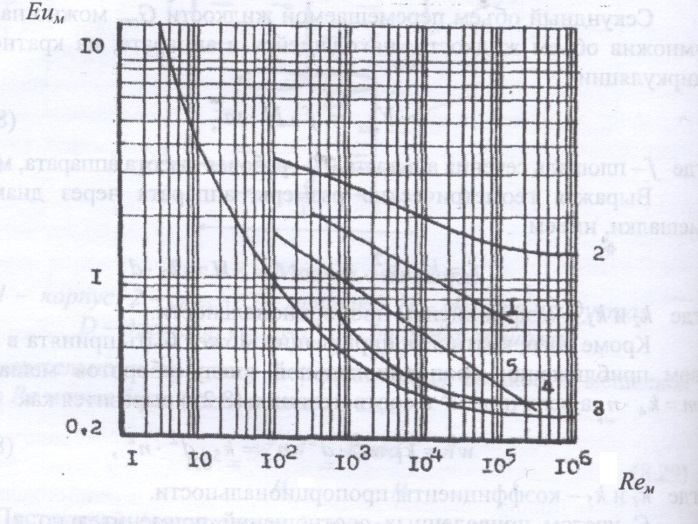
Характеристики перемешивающих устройств разного типа: 1 – лопастная мешалка;

2 – лопастная с змеевиком; 3 – пропеллерная; 4 – турбинная; 5 – якорная.

Моделирование процесса осаждения. Процесс осаждения (выделение твердых частиц из потока жидкости или газа) весьма распространен в пищевой технологии. Физической основой этого процесса служат условия движения одиночных частиц в жидкой среде под действием сил тяжести. В суспензии или в газо – взвеси на частицу действуют следующие силы: сила тяжести: 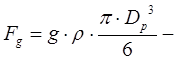и силы вязкого трения:

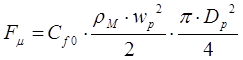
Возможны следующие основные ситуации положения частицы в объеме несущейсреды (жидкости или газа): 1. условия равновесия (витания частиц) 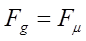2. условия плавания частиц (процесс флотации) 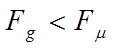и 3) условия осаждения Тогда в условиях равновесия:

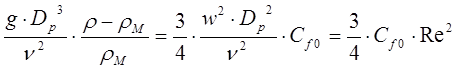так как и число

Архимеда определяется как: условие равновесия в

критериальном виде будет: В процессах осаждения интересует зависимость скорости осаждения от основных факторов. С учетом различных поправок на форму частицы, на ее стесненность движения в ансамбле частиц и др. было получено следующее уравнение: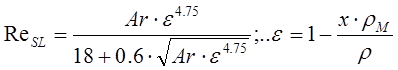

Знание скоростей осаждения позволяет легко найти размеры отстойников в технологической системе. В последней формуле x концентрация частиц в несущей среде.

Моделирование процесса фильтрования.

Ключевую роль в процессе фильтрования играет движение жидкости в пористом слое частиц. Известно, что движение в пористой среде приелимо описывается уравнением фильтрации в различных формах. Наиболее признаны и отработаны это уравнения Дарси и Эргуна. В соответствии с сложившимися представлениями при движении в пористой среде возможны два основных режима: вязкостный, характеризующийся линейной зависимостью от скорости фильтрации и турбулентный, которому соответствует квадратичная форма зависимости потерь давления от скорости фильтрации. В теории фильтрации пользуются понятием скорости фильтрации, которая представляет собой отношение скорости потока к всему

поперечному сечению пористого слоя и определяется по формуле: 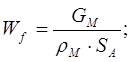В этой формуле обозначены: 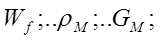скорость фильтрации,

При линейном законе сопротивления в пористой среде (закон Дарси) уравнение,

относящееся к этому закону имеет вид: 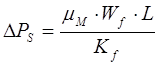в этом уравнении

величина есть коэффициент проницаемости, определяемый по одной из наиболее рекомендуемых формул (Козени) как:

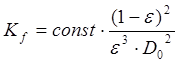
. В формуле для коэффициента проницаемости величины: пористость, характерный (определяющий) размер в пористой среде и эмпирическая константа.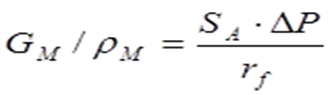

В качестве определяющего размера в пористом слое обычно принимают внешний диаметр частицы. В других случаях это может быть средний размер пор и т.д. Таким образом в линейном законе сопротивления при фильтрации это сопротивление обратно пропорционально квадрату характерного размера пор. Для зернистого слоя роль определяющего размера играет диаметр зерна. Поэтому существует известное положение о том, что сопротивление фильтрующего слоя пропорционально вязкости жидкости и обратно пропорционально квадрату диаметра зерна. На этой основе получено основное кинетическое уравнение процесса фильтрации в виде: Здесь знаменатель правой части есть нечто иное как удельное гидравлическое сопротивление зернистого слоя, которое как это следует из уравнения Дарси определяется следующим образом.

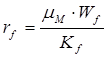
Процессы движения жидких и газовых сред составляют одну из основ многих технологий в ПТС. Полная их классификация чрезвычайно объемна, но возможно выделение наиболее распространенных гидравлических процессов в ПТС. К таким относятся:

1. Гидравлические процессы, связанные с перемещением масс жидкости или газа по гидравлическим (газовым) сетям (трубопроводам, каналам и пр.). Моделирование этих процессов имеет основной своей целью – определение параметров нагнетателей и рабочих режимов трубопроводной сети, в более сложных задачах и определение оптимальных параметров сети, включая форму сети, диаметры трубопроводов и т. д. ит.п.

2. Процессы перемешивания жидких сред с целью создания равномерного распределения компонентов например в суспензиях (жидкость – твердые частицы) или в эмульсиях (жидкость + жидкость – эмульсия) или в пенах (жидкость + газ). И в этих проблемах одна из важнейших задач связана с определением рациональных параметров механизмов перемешивания.

3. Организация процессов разделения несущих сред и распределенных в них частиц, пузырьков, капель и т.д. и т.п. Возможна простейшая организация этих процессов, например – осаждением в поле тяжести, или применением электро – механических или центробежных сил различной формы. Как правило, в таких проблемах необходимо определение геометрии сосудов и параметров механических устройств решающим образом влияющих на процессы разделения.

4.Процессы фильтрования (частный случай процесса разделения). В модели определяются режимы и их параметры (время, геометрия, затраты энергии и др.).

5. Процессы организации псевдо – ожижения и кипящего слоя обычно выбираются для интенсификации тепло – массообмена в системах газ + твердые частицы, газ + жидкость, газ + жидкость + твердые частицы. В этих проблемах задачи моделирования связаны с определением режимных параметров процесса: соотношение объемов фаз и компонентов, создание необходимых уровней скоростей фаз и компонентов, обеспечение равномерных или квази – равномерных распределений фаз и компонентов и др.

6. Организация кавитационных процессов, как мощных средств интенсификации, например при организации гомогенизации на молекулярном уровне, повышении интенсивности массообмена при очистках поверхностей и проч.

7. Процессы массообмена в капиллярно – пористых структурах составляют основу для моделирования таких сложных процессов как экстрагирование, сушка и пр.

8. Процессы перемещения неньютоновских жидкостей могут быть основой многих технологий с теми материалами, которые по своим физическим свойствам не могут считаться «ньютоновскими». В этих случаях моделирование эти особенности должно учитывать. Такой учет скажется и на интегральных параметрах оборудования.

9. Нестационарные процессы гидродинамики проявляются в тех случаях, когда в времени меняются поля скоростей и ускорений.

10. Процессы гидравлики газо – жидкостных систем: движение пузырей и капель в несущей среде; течение жидких пленок; распыление жидкости в газ, истечение газа в жидкость и жидкости в газ; движение двухфазных потоков в каналах и прочее.

11. Процессы гидравлики аппаратов с зернистым (дисперсным) слоем.

12. Нестационарные и переходные процессы в гидравлических системах и многие др.

Гидродинамика (гидромеханика – гидравлика) техническая наука, в которой изучаются законы равновесия и движения жидкостей, а также закономерности взаимодействий между жидкостью и стенками сосудов и трубопроводов, в том числе при движении жидкостей.

Жидкостями называют физические тела, обладающие а) в отличии от твердых тел – текучестью, б) в отличии от газа – малой изменяемостью объема (не сжимаемостью).

Изучение физических явлений в потоках жидкостей и газов сводится к рассмотрению трех видов полей: векторного поля скоростей и ускорений и двух скалярных полей – температуры и концентрации. Механика жидкости в своей основе рассматривает такие фундаментальные понятия как «идеальная жидкость», т.е. жидкость, при движении которой не учитываются вязкие взаимодействия с поверхностями, окружающими жидкость при ее движении. Другое важное понятие – реальная (вязкая) жидкость. Количественно эффект влияния вязкости учитывается введением коэффициентов вязкости динамической 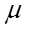[Па * с] и кинематической

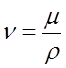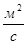[ ]. Понятие вязкость в гидродинамике используют для выделения двух

разных ее типов. Отличают «ньютоновские» и «неньютоновские» жидкости. Для первых предполагается, что сила трения пропорциональна первой степени градиента скорости по нормали и элементарный закон этот описывается соотношением вида:

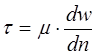где 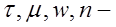напряжения трения, коэффициент динамической вязкости, скорость и нормаль к ней.

• Математические модели гидравлических сетей. Главной задачей расчета гидравлической сети как правило является определение параметров нагнетателя (насоса). Существующие типы сетей удобно разделять на магистральные и разветвленные. Важным моментом выбора нагнетателя является определение его мощности на прокачку теплоносителя. Эта задача решается с помощью известного простого уравнения: 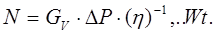Здесь: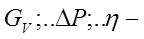

массовый расход теплоносителя, потери напора в гидравлической сети, к.п.д. насоса, соответственно.

Для магистрального трубопровода, в котором диаметр канала не меняется по длине, а местные сопротивления отсутствуют для определения общих потерь давления можно использовать известную из гидравлики формулу:

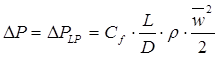В этой формуле 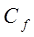коэффициент трения по длине,

формулам: 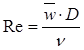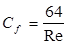для ламинарного режима течения и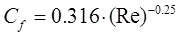

для турбулентного режима. Для сложных, разветвленных трубопроводов, состоящих из системы последовательно соединенных участков, полные потери давления по длине могут определяться как суммы потерь по участкам:

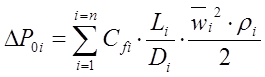Здесь: 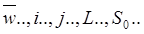средняя скорость и номера отдельных линейных и местных сопротивлений, длины

их, площадь живого сечения, соответственно.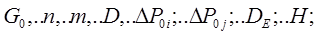

общий массовый расход теплоносителя в трубопроводе, общее число линейных участков и местных сопротивлений, диаметр трубы, полные потери давления по длинам и местным сопротивлениям, эквивалентный диаметр и периметр канала, соответственно. Определение эквивалентного диаметра всегда требуется, когда форма канала не является цилиндрической. Формула по которой это делается имеет следующий вид: 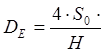В тех задачах, когда заданы располагаемые

потери давления, а объектом расчета является тот допустимый массовый, объемный расход теплоносителя, при котором эти потери не будут превзойдены. Для этих задач из соотношений для потерь давления получены необходимые расчетные формулы - для ламинарного режима: 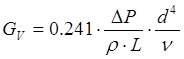и для турбулентного режима: 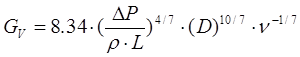это для объемного расхода.

Для расчета разветвленных трубопроводов существенными являются соотношения, определяющие распределения расходов и перепадов давления при параллельном и последовательном их соединении. При параллельном соединении важным является условие равенства потерь давления в параллельных ветвях. Это равенство потерь давления для условий ламинарного течения приводит к следующему соотношению массовых расходов:

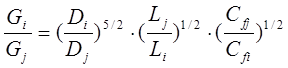
Поскольку известно, что 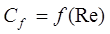и зависит от типа режима, то последующее решение не вызывает затруднений и при двух ветвях для турбулентного режима получим:

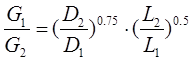и для ламинарного режима имеем: 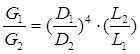Если число параллельных ветвей больше двух, то схема решения не меняется. Она основывается на указанных основных положениях. Т.е. равенство потерь давления и регламентация суммарного расхода.

Выбор нагнетателя. По существу задача выбора нагнетателя сводится к поиску такого решения, когда требования работы трубопроводной системы должны обеспечиваться возможностями нагнетателя (насоса, если перекачивается жидкость). Для трубопроводной системы рабочая характеристика – это зависимость потерь давления от массового расхода. Эта зависимость имеет вид: 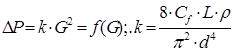Зависимость же массового расхода от создаваемого напора для такого нагнетателя как центробежный насос имеет другую форму: Ниже на графиках показаны различные типичные варианты решения проблемы определения условий совместной работы сети и центробежного насоса. В практике распространены два основных приема управления режимами совместной работы насоса и сети: 1.Когда в характеристику насоса вводится некоторый запас по его напору при сохранении требований о максимально возможном массовом расходе.

2. Когда в отличие от предыдущего варианта такой запас не вводится.

Этим двум вариантам управления согласованием характеристик насоса и сети отвечают два способа их технологической реализации: 1. В первом случае при наличии запаса по напору насоса, в гидравлической схеме насос + сеть вставляют задвижку, позволяющую за счет введения дополнительного гидравлического сопротивления получить нужный массовый расход; 2. В втором случае используют возможности тиристорного управления числом оборотов электродвигателя и за счет этого добиваются полного согласования параметров насоса и сети. Соответствующие этим двум приемам гидравлические схемы показаны ниже:

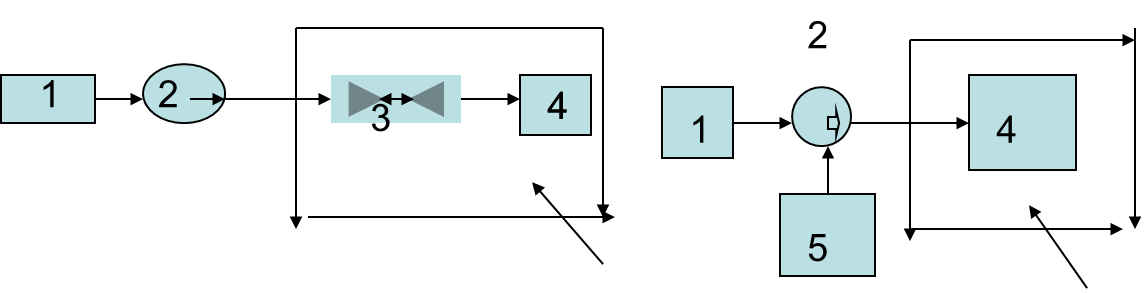
а) б)

Сеть Сеть

Схемы гидравлической разводки. а) Схема регулирования расхода с помощью задвижки; б) Схема регулирования расхода с помощью частотного преобразователя. 1 – Источник жидкости; 2 – насос; 3 – задвижка; 4 – технологический аппарат; 5 – частотный преобразователь.

Ниже представлены типичные графики зависимостей напора и потерь давления от расхода для сети и центробежного насоса и условия их согласования.

Типичная форма согласования рабочих параметров сети и центробежного насоса

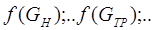= гидравлические характеристики насоса и сети, соответственно.

Ниже на графике показана типичная форма согласования параметров совместной работы насоса и трубопроводной сети. РТ – рабочая точка; н – характеристика насоса; с – характеристика сети. V1, V2, Vp – объемные расходы для различных характеристик сети и данной характеристики насоса.

• Выше приведены рисунки в графической форме, показывающие реализацию процедуры согласования (решения) характеристик насоса и сети (в общем виде) и при разных рабочих характеристиках сети. Ниже в такой же форме представляются различные формы этого согласования при другой схеме управления работой насоса. Когда осуществляется тиристорное управление числом оборотов центробежного насоса. Ниже линия 1 – рабочая линия насоса при номинальном режиме. Линии 2 и 3 при более низких числах оборотов двигателя насоса. Соответственно, видно снижение перекачиваемых объемов теплоносителя.

Перемешивание является широко распространенным и весьма важным процессом пищевых технологий. Типичные целями этого процесса являются:

- создание однородных растворов, суспензий, эмульсий;

- интенсификация процессов теплообмена в аппаратах, физических и химическихреакторах и др.

- интенсификация процессов массообмена (включаяих сочетание с химическими и биохимическими реакциями).

Интенсивность перемешивания определяется количеством энергии, вводимой в единицу объема перемешиваемой среды за единицу времени.

Эффективность перемешивания является важной характеристикой качества процесса. Если при работающем устройстве перемешивания достигается полное смешение фаз в аппарате, т. е. равномерное их распределение по всему объему жидкости, то содержание частиц разных фаз в любой пробе полученной смеси, взятой из разных зон аппарата должно быть равным средней концентрации их в всем аппарате. При недостаточном качестве перемешивание содержание перемешиваемых частиц в различных пробах будет составлять некое распределение. Количественно равномерность распределения частиц (фаз) по всему объему можно выразить следующим соотношением:

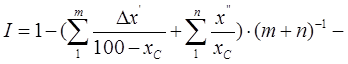здесь: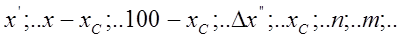

- положительные разности 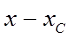; наибольшее возможное положительное значение разности 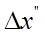; отрицательные разности 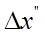наибольшее возможное

(по абсолютной величине) возможное отрицательное значение разности 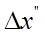; n – число проб, в которых разность 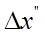отрицательна.

Для количественной характеристики процесса перемешивания используют также методы теории подобия и модифицированные числа Эйлера и Рейнольдса. Здесь определяющая скорость вычисляется по формуле: 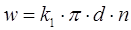число Рейнольдса определяется так:

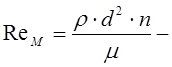
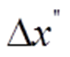В выражении для числа Эйлера величину потерь давления определяют исходя из следующих соображений. Предполагая известными затраты мощности N на

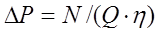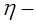процесс перемешивания при известном объемном расходе перемешиваемой жидкости Q, получают для потерь давления при перемешивании следующую связь: здесь к.п.д. насоса. Тогда для числа Эйлера в процессе перемешивания получаем следующее выражение:

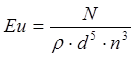Для разных типов мешалок существуют свои характеристики. Вот они.

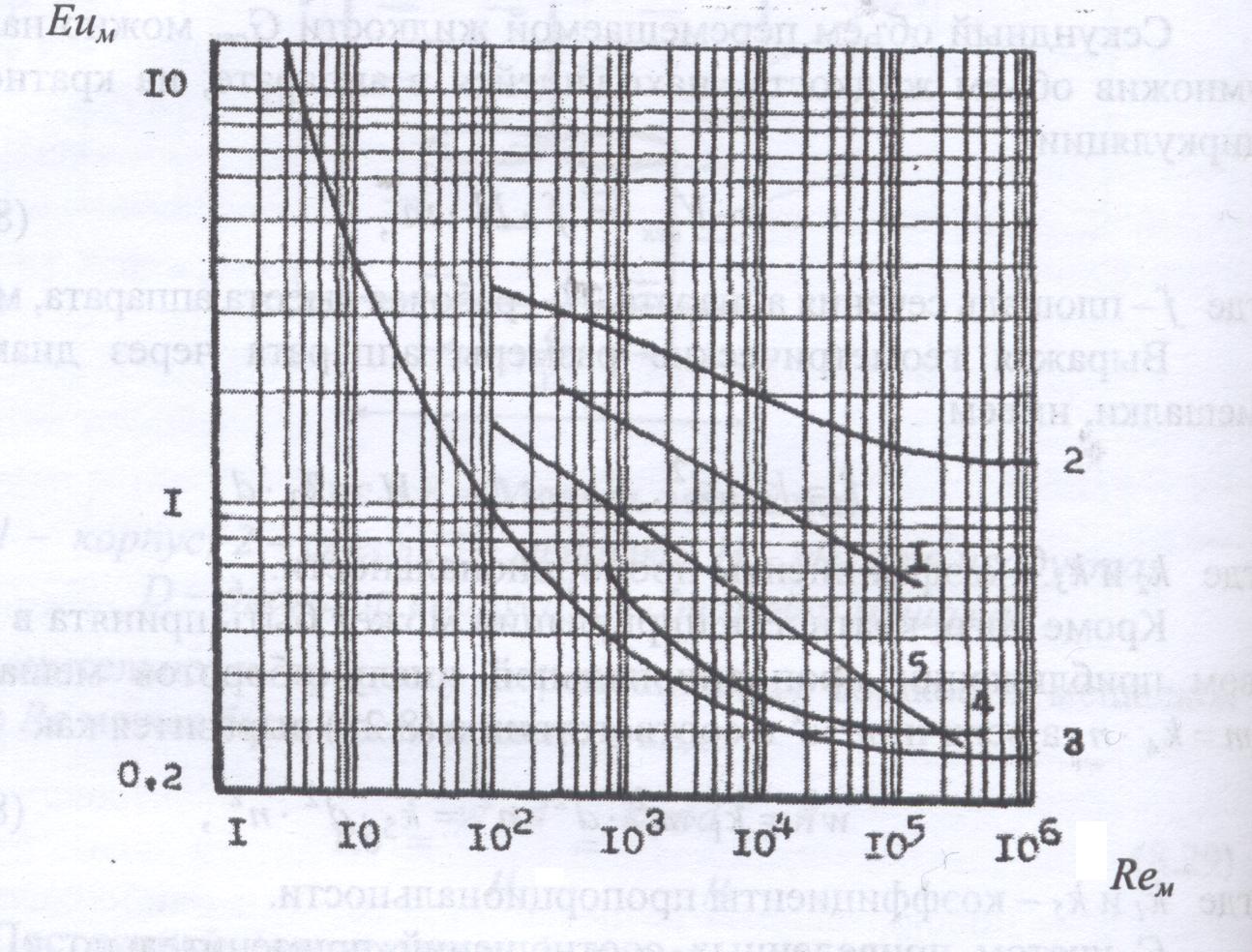
Характеристики перемешивающих устройств разного типа: 1 – лопастная мешалка;

2 – лопастная с змеевиком; 3 – пропеллерная; 4 – турбинная; 5 – якорная.

Моделирование процесса осаждения. Процесс осаждения (выделение твердых частиц из потока жидкости или газа) весьма распространен в пищевой технологии. Физической основой этого процесса служат условия движения одиночных частиц в жидкой среде под действием сил тяжести. В суспензии или в газо – взвеси на частицу действуют следующие силы: сила тяжести: 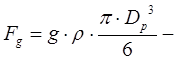и силы вязкого трения: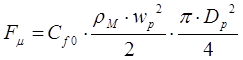

Возможны следующие основные ситуации положения частицы в объеме несущей среды (жидкости или газа): 1. условия равновесия (витания частиц) .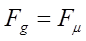

2. условия плавания частиц (процесс флотации) 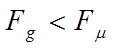и 3) условия осаждения 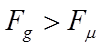Тогда в условиях равновесия: 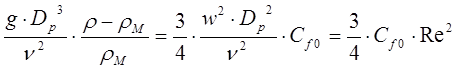так как 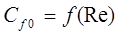и число

Архимеда определяется как: условие равновесия в

критериальном виде будет: 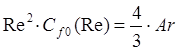В процессах осаждения интересует зависимость скорости осаждения от основных факторов. С учетом различных поправок на форму частицы, на ее стесненность движения в ансамбле частиц и др. было получено следующее уравнение:

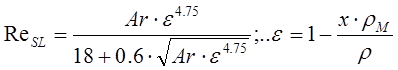
• Знание скоростей осаждения позволяет легко найти размеры отстойников в технологической системе. В последней формуле x концентрация частиц в несущей среде.

Моделирование процесса фильтрования.

Ключевую роль в процессе фильтрования играет движение жидкости в пористом слое частиц. Известно, что движение в пористой среде приелимо описывается уравнением фильтрации в различных формах. Наиболее признаны и отработаны это уравнения Дарси и Эргуна. В соответствии с сложившимися представлениями при движении в пористой среде возможны два основных режима: вязкостный, характеризующийся линейной зависимостью от скорости фильтрации и турбулентный, которому соответствует квадратичная форма зависимости потерь давления от скорости фильтрации. В теории фильтрации пользуются понятием скорости фильтрации, которая представляет собой отношение скорости потока к всему поперечному сечению пористого слоя и определяется по формуле: 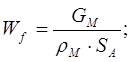В этой формуле обозначены: 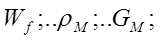скорость фильтрации,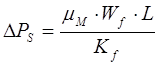

При линейном законе сопротивления в пористой среде (закон Дарси) уравнение, относящееся к этому закону имеет вид: в этом уравнении

величина есть коэффициент проницаемости, определяемый по одной из наиболее рекомендуемых формул (Козени) как: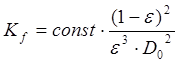

В формуле для коэффициента проницаемости величины: пористость, характерный (определяющий) размер в пористой среде и эмпирическая константа.

В качестве определяющего размера в пористом слое обычно принимают внешний диаметр частицы. В других случаях это может быть средний размер пор и т.д. Таким образом в линейном законе сопротивления при фильтрации это сопротивление обратно пропорционально квадрату характерного размера пор. Для зернистого слоя роль определяющего размера играет диаметр зерна. Поэтому существует известное положение о том, что сопротивление фильтрующего слоя пропорционально вязкости жидкости и обратно пропорционально квадрату диаметра зерна. На этой основе получено основное кинетическое уравнение процесса фильтрации в виде: 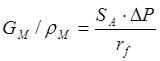Здесь знаменатель правой части

есть нечто иное как удельное гидравлическое сопротивление зернистого слоя, которое как это следует из уравнения Дарси определяется следующим образом.

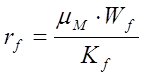Для средней скорости фильтрации располагаем следующим:

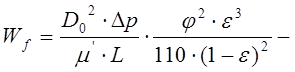В этой формуле величины: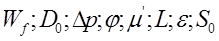

скорость фильтрации; внешний диаметр частиц слоя; потери напора через слой; коэффициент формы; динамическая вязкость жидкости; его толщина; пористость; полное поперечное его сечение, соответственно.

Производительность фильтра определяется с учетом приведенных выше формул так: Зная удельное сопротивление фильтрующего слоя получаем:

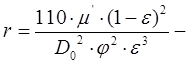
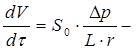Это соотношение рассматривается как основное кинетическое уравнение процесса фильтрации через слой фильтрующего материала.При фильтрации через слой, располагаемый на перегородке уравнение фильтрации:

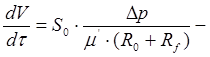Здесь: 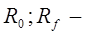гидравлические сопротивления осадка и

фильтра, соответственно.

Дата добавления: 2015-05-23